跳转至

2373. 矩阵中的局部最大值

题目描述

给你一个大小为 n x n 的整数矩阵 grid 。

生成一个大小为 (n - 2) x (n - 2) 的整数矩阵  maxLocal ，并满足：

  • maxLocal[i][j] 等于 grid 中以 i + 1 行和 j + 1 列为中心的 3 x 3 矩阵中的 最大值 。

换句话说，我们希望找出 grid 中每个 3 x 3 矩阵中的最大值。

返回生成的矩阵。

 

示例 1：

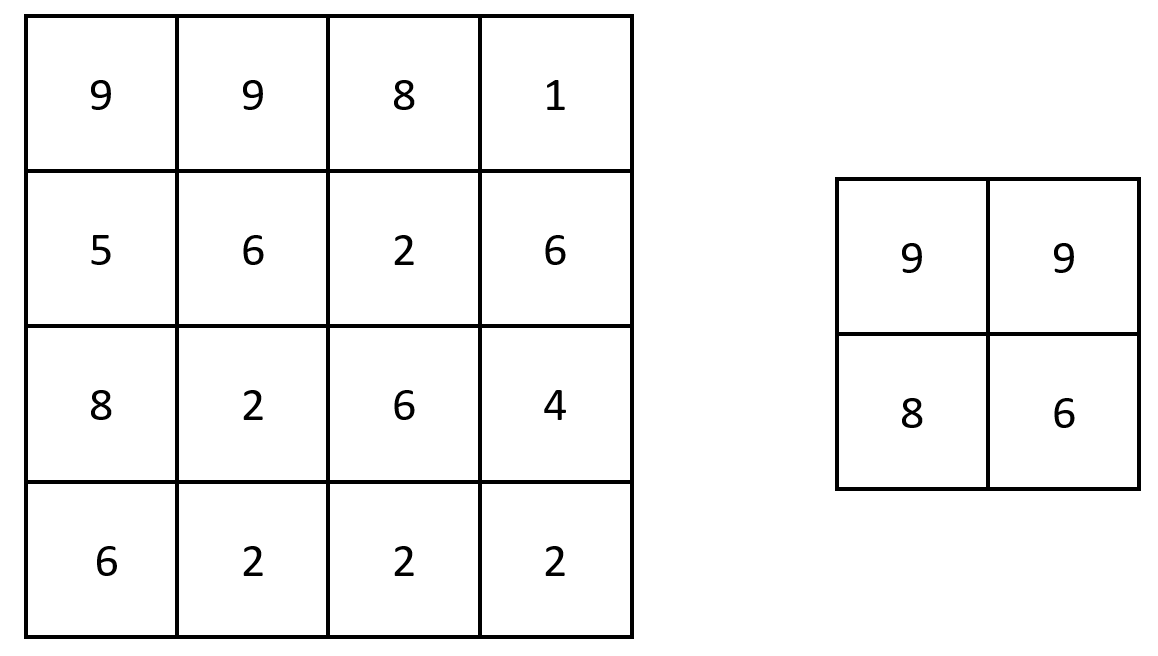
输入：grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
输出：[[9,9],[8,6]]
解释：原矩阵和生成的矩阵如上图所示。
注意，生成的矩阵中，每个值都对应 grid 中一个相接的 3 x 3 矩阵的最大值。

示例 2：

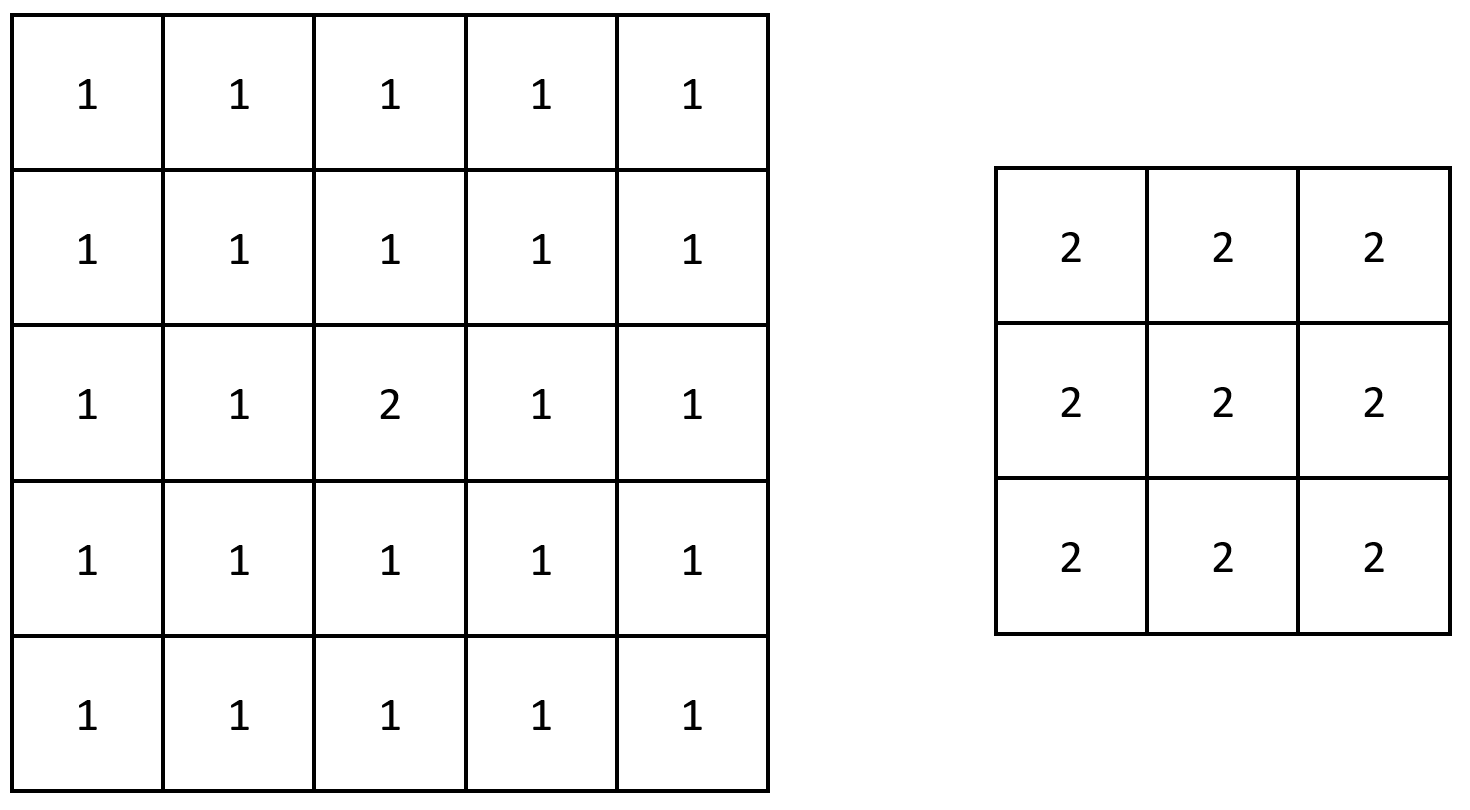
输入：grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
输出：[[2,2,2],[2,2,2],[2,2,2]]
解释：注意，2 包含在 grid 中每个 3 x 3 的矩阵中。

 

提示：

  • n == grid.length == grid[i].length
  • 3 <= n <= 100
  • 1 <= grid[i][j] <= 100

解法

方法一：枚举

我们可以枚举每个 $3 \times 3$ 的矩阵，求出每个 $3 \times 3$ 的矩阵中的最大值，然后将这些最大值放入答案矩阵中。

时间复杂度 $O(n^2)$，其中 $n$ 是矩阵的边长。忽略答案矩阵的空间消耗，空间复杂度 $O(1)$。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
class Solution:
    def largestLocal(self, grid: List[List[int]]) -> List[List[int]]:
        n = len(grid)
        ans = [[0] * (n - 2) for _ in range(n - 2)]
        for i in range(n - 2):
            for j in range(n - 2):
                ans[i][j] = max(
                    grid[x][y] for x in range(i, i + 3) for y in range(j, j + 3)
                )
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution {
    public int[][] largestLocal(int[][] grid) {
        int n = grid.length;
        int[][] ans = new int[n - 2][n - 2];
        for (int i = 0; i < n - 2; ++i) {
            for (int j = 0; j < n - 2; ++j) {
                for (int x = i; x <= i + 2; ++x) {
                    for (int y = j; y <= j + 2; ++y) {
                        ans[i][j] = Math.max(ans[i][j], grid[x][y]);
                    }
                }
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<vector<int>> largestLocal(vector<vector<int>>& grid) {
        int n = grid.size();
        vector<vector<int>> ans(n - 2, vector<int>(n - 2));
        for (int i = 0; i < n - 2; ++i) {
            for (int j = 0; j < n - 2; ++j) {
                for (int x = i; x <= i + 2; ++x) {
                    for (int y = j; y <= j + 2; ++y) {
                        ans[i][j] = max(ans[i][j], grid[x][y]);
                    }
                }
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
func largestLocal(grid [][]int) [][]int {
    n := len(grid)
    ans := make([][]int, n-2)
    for i := range ans {
        ans[i] = make([]int, n-2)
        for j := 0; j < n-2; j++ {
            for x := i; x <= i+2; x++ {
                for y := j; y <= j+2; y++ {
                    ans[i][j] = max(ans[i][j], grid[x][y])
                }
            }
        }
    }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
function largestLocal(grid: number[][]): number[][] {
    const n = grid.length;
    const res = Array.from({ length: n - 2 }, () => new Array(n - 2).fill(0));
    for (let i = 0; i < n - 2; i++) {
        for (let j = 0; j < n - 2; j++) {
            let max = 0;
            for (let k = i; k < i + 3; k++) {
                for (let z = j; z < j + 3; z++) {
                    max = Math.max(max, grid[k][z]);
                }
            }
            res[i][j] = max;
        }
    }
    return res;
}

评论