
题目描述
给定一个包含 不同 正整数的 m × n 整数矩阵 grid。
必须将矩阵中的每一个整数替换为正整数,且满足以下条件:
- 在替换之后,同行或同列中的每两个元素的 相对 顺序应该保持 不变。
- 替换后矩阵中的 最大 数目应尽可能 小。
如果对于原始矩阵中的所有元素对,使 grid[r1][c1] > grid[r2][c2],其中要么 r1 == r2 ,要么 c1 == c2,则相对顺序保持不变。那么在替换之后一定满足 grid[r1][c1] > grid[r2][c2]。
例如,如果 grid = [[2, 4, 5], [7, 3, 9]],那么一个好的替换可以是 grid = [[1, 2, 3], [2, 1, 4]] 或 grid = [[1, 2, 3], [3, 1, 4]]。
返回 结果 矩阵。如果有多个答案,则返回其中 任何 一个。
示例 1:
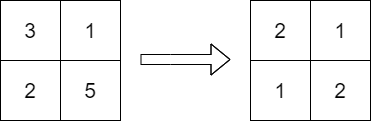
输入: grid = [[3,1],[2,5]]
输出: [[2,1],[1,2]]
解释: 上面的图显示了一个有效的替换。
矩阵中的最大值是 2。可以证明,不能得到更小的值。
示例 2:
输入: grid = [[10]]
输出: [[1]]
解释: 我们将矩阵中唯一的数字替换为 1。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10001 <= m * n <= 1051 <= grid[i][j] <= 109grid 由不同的整数组成。
解法
方法一:排序 + 贪心
由于可以将每一个数字重新填入并且使最终矩阵的最大值最小化,可考虑贪心。
矩阵中每一个数字不一样,可考虑哈希表或数组记录每个数字对应的位置。
将所有数字排序。然后从小到大填入新的数字,每次填入的数字为当前行和列的较大值再加一,同时用新填入的数字更新当前行和列的最大值。
时间复杂度 \(O(mn\log mn)\),空间复杂度 \(O(mn)\)。其中 \(m\) 和 \(n\) 是矩阵的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12 | class Solution:
def minScore(self, grid: List[List[int]]) -> List[List[int]]:
m, n = len(grid), len(grid[0])
nums = [(v, i, j) for i, row in enumerate(grid) for j, v in enumerate(row)]
nums.sort()
row_max = [0] * m
col_max = [0] * n
ans = [[0] * n for _ in range(m)]
for _, i, j in nums:
ans[i][j] = max(row_max[i], col_max[j]) + 1
row_max[i] = col_max[j] = ans[i][j]
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | class Solution {
public int[][] minScore(int[][] grid) {
int m = grid.length, n = grid[0].length;
List<int[]> nums = new ArrayList<>();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
nums.add(new int[] {grid[i][j], i, j});
}
}
Collections.sort(nums, (a, b) -> a[0] - b[0]);
int[] rowMax = new int[m];
int[] colMax = new int[n];
int[][] ans = new int[m][n];
for (int[] num : nums) {
int i = num[1], j = num[2];
ans[i][j] = Math.max(rowMax[i], colMax[j]) + 1;
rowMax[i] = ans[i][j];
colMax[j] = ans[i][j];
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | class Solution {
public:
vector<vector<int>> minScore(vector<vector<int>>& grid) {
vector<tuple<int, int, int>> nums;
int m = grid.size(), n = grid[0].size();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
nums.push_back({grid[i][j], i, j});
}
}
sort(nums.begin(), nums.end());
vector<int> rowMax(m);
vector<int> colMax(n);
vector<vector<int>> ans(m, vector<int>(n));
for (auto [_, i, j] : nums) {
ans[i][j] = max(rowMax[i], colMax[j]) + 1;
rowMax[i] = colMax[j] = ans[i][j];
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | func minScore(grid [][]int) [][]int {
m, n := len(grid), len(grid[0])
nums := [][]int{}
for i, row := range grid {
for j, v := range row {
nums = append(nums, []int{v, i, j})
}
}
sort.Slice(nums, func(i, j int) bool { return nums[i][0] < nums[j][0] })
rowMax := make([]int, m)
colMax := make([]int, n)
ans := make([][]int, m)
for i := range ans {
ans[i] = make([]int, n)
}
for _, num := range nums {
i, j := num[1], num[2]
ans[i][j] = max(rowMax[i], colMax[j]) + 1
rowMax[i] = ans[i][j]
colMax[j] = ans[i][j]
}
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | function minScore(grid: number[][]): number[][] {
const m = grid.length;
const n = grid[0].length;
const nums = [];
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
nums.push([grid[i][j], i, j]);
}
}
nums.sort((a, b) => a[0] - b[0]);
const rowMax = new Array(m).fill(0);
const colMax = new Array(n).fill(0);
const ans = Array.from({ length: m }, _ => new Array(n));
for (const [_, i, j] of nums) {
ans[i][j] = Math.max(rowMax[i], colMax[j]) + 1;
rowMax[i] = colMax[j] = ans[i][j];
}
return ans;
}
|

