
题目描述
城市中的火车有两条路线,分别是常规路线和特快路线。两条路线经过 相同 的 n + 1 个车站,车站编号从 0 到 n。初始时,你位于车站 0 的常规路线。
给你两个 下标从 1 开始 、长度均为 n 的两个整数数组 regular 和 express ,其中 regular[i] 表示乘坐常规路线从车站 i - 1 到车站 i 的费用,express[i] 表示乘坐特快路线从车站 i - 1 到车站 i 的费用。
另外给你一个整数 expressCost,表示从常规路线转换到特快路线的费用。
注意:
- 从特快路线转换回常规路线没有费用。
- 每次 从常规路线转换到特快路线,你都需要支付
expressCost 的费用。
- 留在特快路线上没有额外费用。
返回 下标从 1 开始 、长度为 n 的数组 costs,其中 costs[i] 是从车站 0 到车站 i 的最少费用。
注意:每个车站都可以从任意一条路线 到达 。
示例 1:
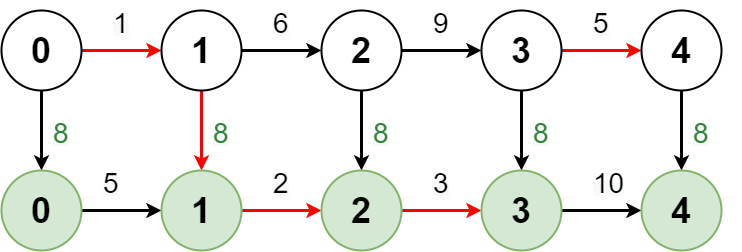
输入:regular = [1,6,9,5], express = [5,2,3,10], expressCost = 8
输出:[1,7,14,19]
解释:上图展示了从车站 0 到车站 4 的最少费用方法。
- 乘坐常规路线从车站 0 到车站 1,费用是 1。
- 乘坐特快路线从车站 1 到车站 2,费用是 8 + 2 = 10。
- 乘坐特快路线从车站 2 到车站 3,费用是 3。
- 乘坐常规路线从车站 3 到车站 4,费用是 5。
总费用是 1 + 10 + 3 + 5 + 19。
注意到达其他车站的最少费用方法可以选择不同的路线。
示例 2:
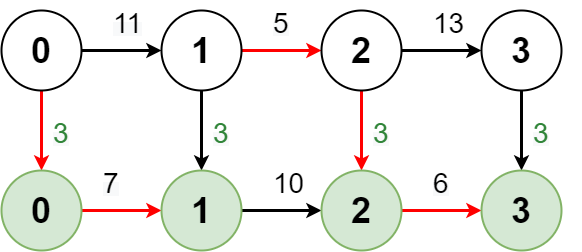
输入:regular = [11,5,13], express = [7,10,6], expressCost = 3
输出:[10,15,24]
解释:上图展示了从车站 0 到车站 3 的最少费用方法。
- 乘坐特快路线从车站 0 到车站 1,费用是 3 + 7 = 10。
- 乘坐常规路线从车站 1 到车站 2,费用是 5。
- 乘坐特快路线从车站 2 到车站 3,费用是 3 + 6 = 9。
总费用是 10 + 5 + 9 = 24。
注意转换回特快路线时需要再次支付 expressCost 的费用。
提示:
n == regular.length == express.length1 <= n <= 1051 <= regular[i], express[i], expressCost <= 105
解法
方法一:动态规划
我们定义 \(f[i]\) 表示从车站 \(0\) 到车站 \(i\) 且到达车站 \(i\) 时乘坐常规路线的最少费用,定义 \(g[i]\) 表示从车站 \(0\) 到车站 \(i\) 且到达车站 \(i\) 时乘坐特快路线的最少费用。初始时 \(f[0]=0, g[0]=\infty\)。
接下来,我们考虑 \(f[i]\) 和 \(g[i]\) 如何进行状态转移。
如果我们到达车站 \(i\) 乘坐的是常规路线,那么我们可以从车站 \(i-1\) 乘坐常规路线或者从车站 \(i-1\) 乘坐特快路线转换到常规路线。因此我们可以得到状态转移方程:
\[
f[i]=\min\{f[i-1]+a_i, g[i-1]+a_i\}
\]
其中 \(a_i\) 表示从车站 \(i-1\) 到车站 \(i\) 乘坐常规路线的费用。
如果我们到达车站 \(i\) 乘坐的是特快路线,那么我们可以从车站 \(i-1\) 乘坐常规路线转换到特快路线或者从车站 \(i-1\) 乘坐特快路线。因此我们可以得到状态转移方程:
\[
g[i]=\min\{f[i-1]+expressCost+b_i, g[i-1]+b_i\}
\]
其中 \(b_i\) 表示从车站 \(i-1\) 到车站 \(i\) 乘坐特快路线的费用。
我们记答案数组为 \(cost\),其中 \(cost[i]\) 表示从车站 \(0\) 到车站 \(i\) 的最少费用。由于我们可以从任意一条路线到达车站 \(i\),因此我们有 \(cost[i]=\min\{f[i], g[i]\}\)。
最后返回 \(cost\) 即可。
时间复杂度 \(O(n)\),空间复杂度 \(O(n)\)。其中 \(n\) 表示车站的数量。
1
2
3
4
5
6
7
8
9
10
11
12
13 | class Solution:
def minimumCosts(
self, regular: List[int], express: List[int], expressCost: int
) -> List[int]:
n = len(regular)
f = [0] * (n + 1)
g = [inf] * (n + 1)
cost = [0] * n
for i, (a, b) in enumerate(zip(regular, express), 1):
f[i] = min(f[i - 1] + a, g[i - 1] + a)
g[i] = min(f[i - 1] + expressCost + b, g[i - 1] + b)
cost[i - 1] = min(f[i], g[i])
return cost
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | class Solution {
public long[] minimumCosts(int[] regular, int[] express, int expressCost) {
int n = regular.length;
long[] f = new long[n + 1];
long[] g = new long[n + 1];
g[0] = 1 << 30;
long[] cost = new long[n];
for (int i = 1; i <= n; ++i) {
int a = regular[i - 1];
int b = express[i - 1];
f[i] = Math.min(f[i - 1] + a, g[i - 1] + a);
g[i] = Math.min(f[i - 1] + expressCost + b, g[i - 1] + b);
cost[i - 1] = Math.min(f[i], g[i]);
}
return cost;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | class Solution {
public:
vector<long long> minimumCosts(vector<int>& regular, vector<int>& express, int expressCost) {
int n = regular.size();
long long f[n + 1];
long long g[n + 1];
f[0] = 0;
g[0] = 1 << 30;
vector<long long> cost(n);
for (int i = 1; i <= n; ++i) {
int a = regular[i - 1];
int b = express[i - 1];
f[i] = min(f[i - 1] + a, g[i - 1] + a);
g[i] = min(f[i - 1] + expressCost + b, g[i - 1] + b);
cost[i - 1] = min(f[i], g[i]);
}
return cost;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | func minimumCosts(regular []int, express []int, expressCost int) []int64 {
n := len(regular)
f := make([]int, n+1)
g := make([]int, n+1)
g[0] = 1 << 30
cost := make([]int64, n)
for i := 1; i <= n; i++ {
a, b := regular[i-1], express[i-1]
f[i] = min(f[i-1]+a, g[i-1]+a)
g[i] = min(f[i-1]+expressCost+b, g[i-1]+b)
cost[i-1] = int64(min(f[i], g[i]))
}
return cost
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | function minimumCosts(regular: number[], express: number[], expressCost: number): number[] {
const n = regular.length;
const f: number[] = new Array(n + 1).fill(0);
const g: number[] = new Array(n + 1).fill(0);
g[0] = 1 << 30;
const cost: number[] = new Array(n).fill(0);
for (let i = 1; i <= n; ++i) {
const [a, b] = [regular[i - 1], express[i - 1]];
f[i] = Math.min(f[i - 1] + a, g[i - 1] + a);
g[i] = Math.min(f[i - 1] + expressCost + b, g[i - 1] + b);
cost[i - 1] = Math.min(f[i], g[i]);
}
return cost;
}
|
我们注意到 \(f[i]\) 和 \(g[i]\) 的状态转移方程中,我们只需要用到 \(f[i-1]\) 和 \(g[i-1]\),因此我们可以使用两个变量 \(f\) 和 \(g\) 分别记录 \(f[i-1]\) 和 \(g[i-1]\) 的值,这样可以将空间复杂度优化到 \(O(1)\)。
1
2
3
4
5
6
7
8
9
10
11
12
13 | class Solution:
def minimumCosts(
self, regular: List[int], express: List[int], expressCost: int
) -> List[int]:
n = len(regular)
f, g = 0, inf
cost = [0] * n
for i, (a, b) in enumerate(zip(regular, express), 1):
ff = min(f + a, g + a)
gg = min(f + expressCost + b, g + b)
f, g = ff, gg
cost[i - 1] = min(f, g)
return cost
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | class Solution {
public long[] minimumCosts(int[] regular, int[] express, int expressCost) {
int n = regular.length;
long f = 0;
long g = 1 << 30;
long[] cost = new long[n];
for (int i = 0; i < n; ++i) {
int a = regular[i];
int b = express[i];
long ff = Math.min(f + a, g + a);
long gg = Math.min(f + expressCost + b, g + b);
f = ff;
g = gg;
cost[i] = Math.min(f, g);
}
return cost;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | class Solution {
public:
vector<long long> minimumCosts(vector<int>& regular, vector<int>& express, int expressCost) {
int n = regular.size();
long long f = 0;
long long g = 1 << 30;
vector<long long> cost(n);
for (int i = 0; i < n; ++i) {
int a = regular[i];
int b = express[i];
long long ff = min(f + a, g + a);
long long gg = min(f + expressCost + b, g + b);
f = ff;
g = gg;
cost[i] = min(f, g);
}
return cost;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12 | func minimumCosts(regular []int, express []int, expressCost int) []int64 {
f, g := 0, 1<<30
cost := make([]int64, len(regular))
for i, a := range regular {
b := express[i]
ff := min(f+a, g+a)
gg := min(f+expressCost+b, g+b)
f, g = ff, gg
cost[i] = int64(min(f, g))
}
return cost
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | function minimumCosts(regular: number[], express: number[], expressCost: number): number[] {
const n = regular.length;
let f = 0;
let g = 1 << 30;
const cost: number[] = new Array(n).fill(0);
for (let i = 0; i < n; ++i) {
const [a, b] = [regular[i], express[i]];
const ff = Math.min(f + a, g + a);
const gg = Math.min(f + expressCost + b, g + b);
[f, g] = [ff, gg];
cost[i] = Math.min(f, g);
}
return cost;
}
|


