2293. 极大极小游戏

题目描述

给你一个下标从 0 开始的整数数组 nums ，其长度是 2 的幂。

对 nums 执行下述算法：

设 n 等于 nums 的长度，如果 n == 1 ，终止算法过程。否则，创建一个新的整数数组 newNums ，新数组长度为 n / 2 ，下标从 0 开始。
对于满足 0 <= i < n / 2 的每个偶数下标 i ，将 newNums[i] 赋值为 min(nums[2 * i], nums[2 * i + 1]) 。
对于满足 0 <= i < n / 2 的每个奇数下标 i ，将 newNums[i] 赋值为 max(nums[2 * i], nums[2 * i + 1]) 。
用 newNums 替换 nums 。
从步骤 1 开始重复整个过程。

执行算法后，返回 nums 中剩下的那个数字。

示例 1：

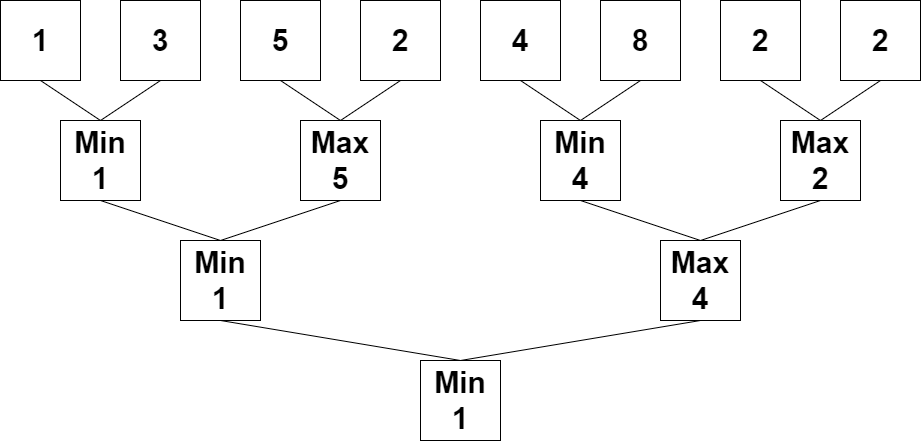
输入：nums = [1,3,5,2,4,8,2,2]
输出：1
解释：重复执行算法会得到下述数组。
第一轮：nums = [1,5,4,2]
第二轮：nums = [1,4]
第三轮：nums = [1]
1 是最后剩下的那个数字，返回 1 。

示例 2：

输入：nums = [3]
输出：3
解释：3 就是最后剩下的数字，返回 3 。

提示：

1 <= nums.length <= 1024
1 <= nums[i] <= 10⁹
nums.length 是 2 的幂

解法

方法一：模拟

根据题意，我们可以模拟整个过程，最后剩下的数字即为答案。在实现上，我们不需要额外创建数组，直接在原数组上进行操作即可。

时间复杂度 $O(n)$，其中 $n$ 是数组 $\textit{nums}$ 的长度。空间复杂度 $O(1)$。

Python3JavaC++GoTypeScriptRustC

class Solution:
    def minMaxGame(self, nums: List[int]) -> int:
        n = len(nums)
        while n > 1:
            n >>= 1
            for i in range(n):
                a, b = nums[i << 1], nums[i << 1 | 1]
                nums[i] = min(a, b) if i % 2 == 0 else max(a, b)
        return nums[0]

class Solution {
    public int minMaxGame(int[] nums) {
        for (int n = nums.length; n > 1;) {
            n >>= 1;
            for (int i = 0; i < n; ++i) {
                int a = nums[i << 1], b = nums[i << 1 | 1];
                nums[i] = i % 2 == 0 ? Math.min(a, b) : Math.max(a, b);
            }
        }
        return nums[0];
    }
}

class Solution {
public:
    int minMaxGame(vector<int>& nums) {
        for (int n = nums.size(); n > 1;) {
            n >>= 1;
            for (int i = 0; i < n; ++i) {
                int a = nums[i << 1], b = nums[i << 1 | 1];
                nums[i] = i % 2 == 0 ? min(a, b) : max(a, b);
            }
        }
        return nums[0];
    }
};

func minMaxGame(nums []int) int {
    for n := len(nums); n > 1; {
        n >>= 1
        for i := 0; i < n; i++ {
            a, b := nums[i<<1], nums[i<<1|1]
            if i%2 == 0 {
                nums[i] = min(a, b)
            } else {
                nums[i] = max(a, b)
            }
        }
    }
    return nums[0]
}

function minMaxGame(nums: number[]): number {
    for (let n = nums.length; n > 1; ) {
        n >>= 1;
        for (let i = 0; i < n; ++i) {
            const a = nums[i << 1];
            const b = nums[(i << 1) | 1];
            nums[i] = i % 2 == 0 ? Math.min(a, b) : Math.max(a, b);
        }
    }
    return nums[0];
}

impl Solution {
    pub fn min_max_game(mut nums: Vec<i32>) -> i32 {
        let mut n = nums.len();
        while n != 1 {
            n >>= 1;
            for i in 0..n {
                nums[i] = (if (i & 1) == 1 { i32::max } else { i32::min })(
                    nums[i << 1],
                    nums[(i << 1) | 1],
                );
            }
        }
        nums[0]
    }
}

#define min(a, b) (((a) < (b)) ? (a) : (b))
#define max(a, b) (((a) > (b)) ? (a) : (b))

int minMaxGame(int* nums, int numsSize) {
    while (numsSize != 1) {
        numsSize >>= 1;
        for (int i = 0; i < numsSize; i++) {
            int a = nums[i << 1];
            int b = nums[i << 1 | 1];
            nums[i] = i & 1 ? max(a, b) : min(a, b);
        }
    }
    return nums[0];
}

2293. 极大极小游戏

题目描述

解法

方法一：模拟

评论