2285. 道路的最大总重要性

题目描述

给你一个整数 n ，表示一个国家里的城市数目。城市编号为 0 到 n - 1 。

给你一个二维整数数组 roads ，其中 roads[i] = [a_i, b_i] 表示城市 a_i 和 b_i 之间有一条双向道路。

你需要给每个城市安排一个从 1 到 n 之间的整数值，且每个值只能被使用一次。道路的 重要性 定义为这条道路连接的两座城市数值之和。

请你返回在最优安排下，所有道路重要性 之和最大为多少。

示例 1：

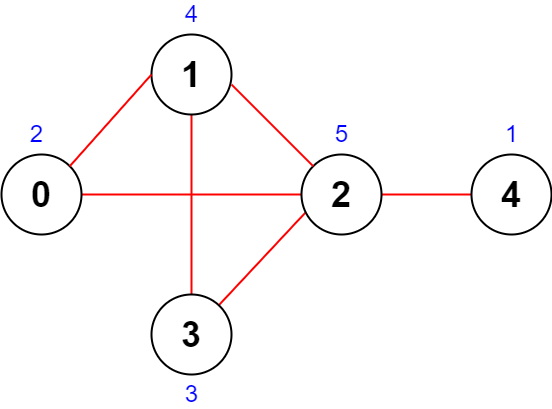
输入：n = 5, roads = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
输出：43
解释：上图展示了国家图和每个城市被安排的值 [2,4,5,3,1] 。
- 道路 (0,1) 重要性为 2 + 4 = 6 。
- 道路 (1,2) 重要性为 4 + 5 = 9 。
- 道路 (2,3) 重要性为 5 + 3 = 8 。
- 道路 (0,2) 重要性为 2 + 5 = 7 。
- 道路 (1,3) 重要性为 4 + 3 = 7 。
- 道路 (2,4) 重要性为 5 + 1 = 6 。
所有道路重要性之和为 6 + 9 + 8 + 7 + 7 + 6 = 43 。
可以证明，重要性之和不可能超过 43 。

示例 2：

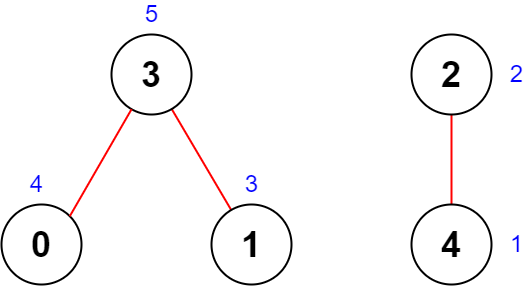
输入：n = 5, roads = [[0,3],[2,4],[1,3]]
输出：20
解释：上图展示了国家图和每个城市被安排的值 [4,3,2,5,1] 。
- 道路 (0,3) 重要性为 4 + 5 = 9 。
- 道路 (2,4) 重要性为 2 + 1 = 3 。
- 道路 (1,3) 重要性为 3 + 5 = 8 。
所有道路重要性之和为 9 + 3 + 8 = 20 。
可以证明，重要性之和不可能超过 20 。

提示：

2 <= n <= 5 * 10⁴
1 <= roads.length <= 5 * 10⁴
roads[i].length == 2
0 <= a_i, b_i <= n - 1
a_i != b_i
没有重复道路。

解法

方法一：贪心 + 排序

我们考虑每个城市对所有道路的总重要性的贡献度，记录在数组 $\textit{deg}$ 中。然后将 $\textit{deg}$ 按贡献度从小到大排序，为城市依次分配 $[1, 2, ..., n]$。

时间复杂度 $O(n \times \log n)$，空间复杂度 $O(n)$。

Python3JavaC++GoTypeScript

class Solution:
    def maximumImportance(self, n: int, roads: List[List[int]]) -> int:
        deg = [0] * n
        for a, b in roads:
            deg[a] += 1
            deg[b] += 1
        deg.sort()
        return sum(i * v for i, v in enumerate(deg, 1))

class Solution {
    public long maximumImportance(int n, int[][] roads) {
        int[] deg = new int[n];
        for (int[] r : roads) {
            ++deg[r[0]];
            ++deg[r[1]];
        }
        Arrays.sort(deg);
        long ans = 0;
        for (int i = 0; i < n; ++i) {
            ans += (long) (i + 1) * deg[i];
        }
        return ans;
    }
}

class Solution {
public:
    long long maximumImportance(int n, vector<vector<int>>& roads) {
        vector<int> deg(n);
        for (auto& r : roads) {
            ++deg[r[0]];
            ++deg[r[1]];
        }
        sort(deg.begin(), deg.end());
        long long ans = 0;
        for (int i = 0; i < n; ++i) {
            ans += (i + 1LL) * deg[i];
        }
        return ans;
    }
};

func maximumImportance(n int, roads [][]int) (ans int64) {
    deg := make([]int, n)
    for _, r := range roads {
        deg[r[0]]++
        deg[r[1]]++
    }
    sort.Ints(deg)
    for i, x := range deg {
        ans += int64(x) * int64(i+1)
    }
    return
}

function maximumImportance(n: number, roads: number[][]): number {
    const deg: number[] = Array(n).fill(0);
    for (const [a, b] of roads) {
        ++deg[a];
        ++deg[b];
    }
    deg.sort((a, b) => a - b);
    return deg.reduce((acc, cur, idx) => acc + (idx + 1) * cur, 0);
}

2285. 道路的最大总重要性

题目描述

解法

方法一：贪心 + 排序

评论