2237. 计算街道上满足所需亮度的位置数量 🔒

题目描述

给你一个整数 n。一条完全笔直的街道用一条从 0 到 n - 1 的数轴表示。给你一个二维整数数组 lights，表示街道上的路灯。每个 lights[i] = [position_i, range_i] 表示在位置 position_i 有一盏路灯，从 [max(0, position_i - range_i), min(n - 1, position_i + range_i)] (包含边界) 开始照亮该区域。

位置 p 的亮度定义为点亮位置 p 的路灯的数量。给定一个大小为 n 的整数数组 requirement，数组的 下标从 0 开始，其中 requirement[i] 是街道上第 i 个位置的最小亮度。

返回街道上 0 到 n - 1 之间 亮度至少满足 requirement[i] 的位置 i 的数量。

示例 1:

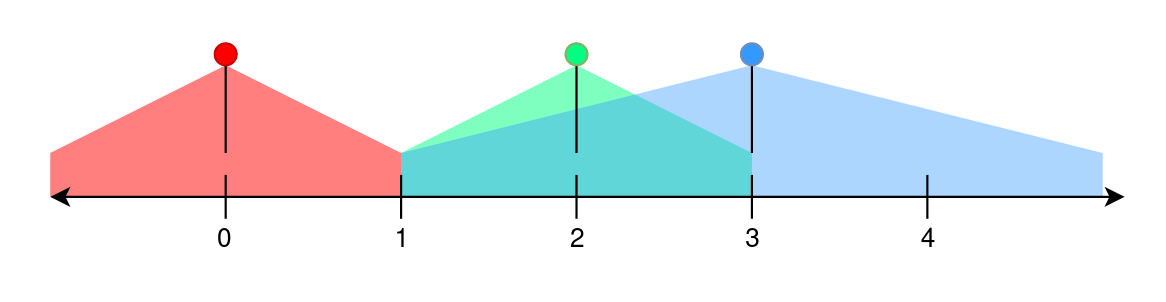
输入: n = 5, lights = [[0,1],[2,1],[3,2]], requirement = [0,2,1,4,1]
输出: 4
解释:
- 第一盏路灯照亮区域范围为 [max(0,0 - 1)， min(n - 1,0 + 1)] =[0,1](含边界)。
- 第二盏路灯的点亮范围为 [max(0,2 - 1)， min(n - 1,2 + 1)] =[1,3](含边界)。
- 第三盏路灯照亮区域范围为 [max(0,3 - 2)， min(n - 1,3 + 2)] =[1,4](含边界)。

-   位置 0 被第一盏路灯覆盖。它被 1 个路灯覆盖，大于 requirement[0]。
-   位置 1 被第一、第二和第三个路灯覆盖。被 3 个路灯覆盖，大于 requirement[1]。
-   位置 2 由第二和第三路灯覆盖。被 2 个路灯覆盖，大于 requirement[2]。
-   位置 3 由第二和第三路灯覆盖。它被 2 个路灯覆盖，比 requirement[3] 少。
-   位置 4 被第三个路灯覆盖。它被 1 盏路灯覆盖，等于 requirement[4]。

位置 0、1、2、4 满足要求，因此返回 4。

示例 2:

输入: n = 1, lights = [[0,1]], requirement = [2]
输出: 0
解释:
- 第一盏路灯照亮区域范围为 [max(0,0 - 1)， min(n - 1,0 + 1)] =[0,0](含边界)。
- 位置 0 被第一盏路灯覆盖。它被 1 个路灯覆盖，比 requirement[0] 少。
- 返回0，因为没有位置满足亮度要求。

提示:

1 <= n <= 10⁵
1 <= lights.length <= 10⁵
0 <= position_i < n
0 <= range_i <= 10⁵
requirement.length == n
0 <= requirement[i] <= 10⁵

解法

方法一：差分数组

时间复杂度 $O(n)$。

Python3JavaC++Go

class Solution:
    def meetRequirement(
        self, n: int, lights: List[List[int]], requirement: List[int]
    ) -> int:
        d = [0] * 100010
        for p, r in lights:
            i, j = max(0, p - r), min(n - 1, p + r)
            d[i] += 1
            d[j + 1] -= 1
        return sum(s >= r for s, r in zip(accumulate(d), requirement))

class Solution {
    public int meetRequirement(int n, int[][] lights, int[] requirement) {
        int[] d = new int[100010];
        for (int[] e : lights) {
            int i = Math.max(0, e[0] - e[1]);
            int j = Math.min(n - 1, e[0] + e[1]);
            ++d[i];
            --d[j + 1];
        }
        int s = 0;
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            s += d[i];
            if (s >= requirement[i]) {
                ++ans;
            }
        }
        return ans;
    }
}

class Solution {
public:
    int meetRequirement(int n, vector<vector<int>>& lights, vector<int>& requirement) {
        vector<int> d(100010);
        for (auto& e : lights) {
            int i = max(0, e[0] - e[1]), j = min(n - 1, e[0] + e[1]);
            ++d[i];
            --d[j + 1];
        }
        int s = 0, ans = 0;
        for (int i = 0; i < n; ++i) {
            s += d[i];
            if (s >= requirement[i]) ++ans;
        }
        return ans;
    }
};

func meetRequirement(n int, lights [][]int, requirement []int) int {
    d := make([]int, 100010)
    for _, e := range lights {
        i, j := max(0, e[0]-e[1]), min(n-1, e[0]+e[1])
        d[i]++
        d[j+1]--
    }
    var s, ans int
    for i, r := range requirement {
        s += d[i]
        if s >= r {
            ans++
        }
    }
    return ans
}

2237. 计算街道上满足所需亮度的位置数量 🔒

题目描述

解法

方法一：差分数组

评论