哈希表
数组
模拟
题目描述
存在一个 n x n 大小、下标从 0 开始的网格,网格中埋着一些工件。给你一个整数 n 和一个下标从 0 开始的二维整数数组 artifacts ,artifacts 描述了矩形工件的位置,其中 artifacts[i] = [r1i , c1i , r2i , c2i ] 表示第 i 个工件在子网格中的填埋情况:
(r1i , c1i ) 是第 i 个工件 左上 单元格的坐标,且(r2i , c2i ) 是第 i 个工件 右下 单元格的坐标。
你将会挖掘网格中的一些单元格,并清除其中的填埋物。如果单元格中埋着工件的一部分,那么该工件这一部分将会裸露出来。如果一个工件的所有部分都都裸露出来,你就可以提取该工件。
给你一个下标从 0 开始的二维整数数组 dig ,其中 dig[i] = [ri , ci ] 表示你将会挖掘单元格 (ri , ci ) ,返回你可以提取的工件数目。
生成的测试用例满足:
不存在重叠的两个工件。
每个工件最多只覆盖 4 个单元格。
dig 中的元素互不相同。
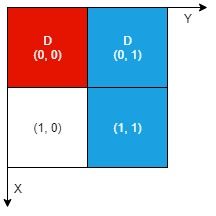
示例 1:
输入: n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1]]
输出: 1
解释:
不同颜色表示不同的工件。挖掘的单元格用 'D' 在网格中进行标记。
有 1 个工件可以提取,即红色工件。
蓝色工件在单元格 (1,1) 的部分尚未裸露出来,所以无法提取该工件。
因此,返回 1 。
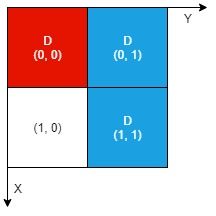
示例 2:
输入: n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1],[1,1]]
输出: 2
解释: 红色工件和蓝色工件的所有部分都裸露出来(用 'D' 标记),都可以提取。因此,返回 2 。
提示:
1 <= n <= 10001 <= artifacts.length, dig.length <= min(n2 , 105 )artifacts[i].length == 4dig[i].length == 20 <= r1i , c1i , r2i , c2i , ri , ci <= n - 1r1i <= r2i c1i <= c2i 不存在重叠的两个工件
每个工件 最多 只覆盖 4 个单元格
dig 中的元素互不相同
解法
方法一:哈希表
我们可以用哈希表 \(s\) 记录所有挖掘的单元格,然后遍历所有工件,判断工件的所有部分是否都在哈希表中,若是则可以提取该工件,答案加一。
时间复杂度 \(O(m + k)\) ,空间复杂度 \(O(k)\) ,其中 \(m\) 是工件的数量,而 \(k\) 是挖掘的单元格的数量。
Python3 Java C++ Go TypeScript Rust
1
2
3
4
5
6
7
8
9
10
11
12 class Solution :
def digArtifacts (
self , n : int , artifacts : List [ List [ int ]], dig : List [ List [ int ]]
) -> int :
def check ( a : List [ int ]) -> bool :
x1 , y1 , x2 , y2 = a
return all (
( x , y ) in s for x in range ( x1 , x2 + 1 ) for y in range ( y1 , y2 + 1 )
)
s = {( i , j ) for i , j in dig }
return sum ( check ( a ) for a in artifacts )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 class Solution {
private Set < Integer > s = new HashSet <> ();
private int n ;
public int digArtifacts ( int n , int [][] artifacts , int [][] dig ) {
this . n = n ;
for ( var p : dig ) {
s . add ( p [ 0 ] * n + p [ 1 ] );
}
int ans = 0 ;
for ( var a : artifacts ) {
ans += check ( a );
}
return ans ;
}
private int check ( int [] a ) {
int x1 = a [ 0 ] , y1 = a [ 1 ] , x2 = a [ 2 ] , y2 = a [ 3 ] ;
for ( int x = x1 ; x <= x2 ; ++ x ) {
for ( int y = y1 ; y <= y2 ; ++ y ) {
if ( ! s . contains ( x * n + y )) {
return 0 ;
}
}
}
return 1 ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 class Solution {
public :
int digArtifacts ( int n , vector < vector < int >>& artifacts , vector < vector < int >>& dig ) {
unordered_set < int > s ;
for ( auto & p : dig ) {
s . insert ( p [ 0 ] * n + p [ 1 ]);
}
auto check = [ & ]( vector < int >& a ) {
int x1 = a [ 0 ], y1 = a [ 1 ], x2 = a [ 2 ], y2 = a [ 3 ];
for ( int x = x1 ; x <= x2 ; ++ x ) {
for ( int y = y1 ; y <= y2 ; ++ y ) {
if ( ! s . count ( x * n + y )) {
return 0 ;
}
}
}
return 1 ;
};
int ans = 0 ;
for ( auto & a : artifacts ) {
ans += check ( a );
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 func digArtifacts ( n int , artifacts [][] int , dig [][] int ) ( ans int ) {
s := map [ int ] bool {}
for _ , p := range dig {
s [ p [ 0 ] * n + p [ 1 ]] = true
}
check := func ( a [] int ) int {
x1 , y1 , x2 , y2 := a [ 0 ], a [ 1 ], a [ 2 ], a [ 3 ]
for x := x1 ; x <= x2 ; x ++ {
for y := y1 ; y <= y2 ; y ++ {
if ! s [ x * n + y ] {
return 0
}
}
}
return 1
}
for _ , a := range artifacts {
ans += check ( a )
}
return
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 function digArtifacts ( n : number , artifacts : number [][], dig : number [][]) : number {
const s : Set < number > = new Set ();
for ( const [ x , y ] of dig ) {
s . add ( x * n + y );
}
let ans = 0 ;
const check = ( a : number []) : number => {
const [ x1 , y1 , x2 , y2 ] = a ;
for ( let x = x1 ; x <= x2 ; ++ x ) {
for ( let y = y1 ; y <= y2 ; ++ y ) {
if ( ! s . has ( x * n + y )) {
return 0 ;
}
}
}
return 1 ;
};
for ( const a of artifacts ) {
ans += check ( a );
}
return ans ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 use std :: collections :: HashSet ;
impl Solution {
pub fn dig_artifacts ( n : i32 , artifacts : Vec < Vec < i32 >> , dig : Vec < Vec < i32 >> ) -> i32 {
let mut s : HashSet < i32 > = HashSet :: new ();
for p in dig {
s . insert ( p [ 0 ] * n + p [ 1 ]);
}
let check = | a : & [ i32 ] | -> i32 {
let x1 = a [ 0 ];
let y1 = a [ 1 ];
let x2 = a [ 2 ];
let y2 = a [ 3 ];
for x in x1 ..= x2 {
for y in y1 ..= y2 {
if ! s . contains ( & ( x * n + y )) {
return 0 ;
}
}
}
1
};
let mut ans = 0 ;
for a in artifacts {
ans += check ( & a );
}
ans
}
}