二叉树
哈希表
数组
树
题目描述
给你一个二维整数数组 descriptions ,其中 descriptions[i] = [parenti , childi , isLefti ] 表示 parenti 是 childi 在 二叉树 中的 父节点 ,二叉树中各节点的值 互不相同 。此外:
如果 isLefti == 1 ,那么 childi 就是 parenti 的左子节点。
如果 isLefti == 0 ,那么 childi 就是 parenti 的右子节点。
请你根据 descriptions 的描述来构造二叉树并返回其 根节点 。
测试用例会保证可以构造出 有效 的二叉树。
示例 1:
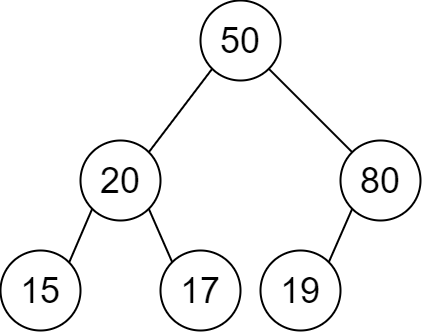
输入: descriptions = [[20,15,1],[20,17,0],[50,20,1],[50,80,0],[80,19,1]]
输出: [50,20,80,15,17,19]
解释: 根节点是值为 50 的节点,因为它没有父节点。
结果二叉树如上图所示。
示例 2:
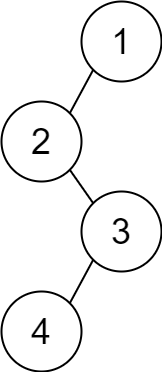
输入: descriptions = [[1,2,1],[2,3,0],[3,4,1]]
输出: [1,2,null,null,3,4]
解释: 根节点是值为 1 的节点,因为它没有父节点。
结果二叉树如上图所示。
提示:
1 <= descriptions.length <= 104 descriptions[i].length == 31 <= parenti , childi <= 105 0 <= isLefti <= 1descriptions 所描述的二叉树是一棵有效二叉树
解法
方法一:哈希表
我们可以用一个哈希表 \(\textit{nodes}\) 来存储所有节点,其中键为节点的值,值为节点本身,用一个集合 \(\textit{children}\) 来存储所有的子节点。
遍历 \(\textit{descriptions}\) ,对于每个描述 \([\textit{parent}, \textit{child}, \textit{isLeft}]\) ,如果 \(\textit{parent}\) 不在 \(\textit{nodes}\) 中,我们就将 \(\textit{parent}\) 加入 \(\textit{nodes}\) ,并初始化一个值为 \(\textit{parent}\) 的节点。如果 \(\textit{child}\) 不在 \(\textit{nodes}\) 中,我们就将 \(\textit{child}\) 加入 \(\textit{nodes}\) ,并初始化一个值为 \(\textit{child}\) 的节点。然后我们将 \(\textit{child}\) 加入 \(\textit{children}\) 。
如果 \(\textit{isLeft}\) 为真,我们就将 \(\textit{child}\) 作为 \(\textit{parent}\) 的左子节点,否则我们就将 \(\textit{child}\) 作为 \(\textit{parent}\) 的右子节点。
最后,我们遍历 \(\textit{nodes}\) ,如果某个节点的值不在 \(\textit{children}\) 中,那么这个节点就是根节点,我们返回这个节点。
时间复杂度 \(O(n)\) ,空间复杂度 \(O(n)\) 。其中 \(n\) 是 \(\textit{descriptions}\) 的长度。
Python3 Java C++ Go TypeScript Rust JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution :
def createBinaryTree ( self , descriptions : List [ List [ int ]]) -> Optional [ TreeNode ]:
nodes = defaultdict ( TreeNode )
children = set ()
for parent , child , isLeft in descriptions :
if parent not in nodes :
nodes [ parent ] = TreeNode ( parent )
if child not in nodes :
nodes [ child ] = TreeNode ( child )
children . add ( child )
if isLeft :
nodes [ parent ] . left = nodes [ child ]
else :
nodes [ parent ] . right = nodes [ child ]
root = ( set ( nodes . keys ()) - children ) . pop ()
return nodes [ root ]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode createBinaryTree ( int [][] descriptions ) {
Map < Integer , TreeNode > nodes = new HashMap <> ();
Set < Integer > children = new HashSet <> ();
for ( var d : descriptions ) {
int parent = d [ 0 ] , child = d [ 1 ] , isLeft = d [ 2 ] ;
if ( ! nodes . containsKey ( parent )) {
nodes . put ( parent , new TreeNode ( parent ));
}
if ( ! nodes . containsKey ( child )) {
nodes . put ( child , new TreeNode ( child ));
}
if ( isLeft == 1 ) {
nodes . get ( parent ). left = nodes . get ( child );
} else {
nodes . get ( parent ). right = nodes . get ( child );
}
children . add ( child );
}
for ( var e : nodes . entrySet ()) {
if ( ! children . contains ( e . getKey ())) {
return e . getValue ();
}
}
return null ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public :
TreeNode * createBinaryTree ( vector < vector < int >>& descriptions ) {
unordered_map < int , TreeNode *> nodes ;
unordered_set < int > children ;
for ( const auto & d : descriptions ) {
int parent = d [ 0 ], child = d [ 1 ], isLeft = d [ 2 ];
if ( ! nodes . contains ( parent )) {
nodes [ parent ] = new TreeNode ( parent );
}
if ( ! nodes . contains ( child )) {
nodes [ child ] = new TreeNode ( child );
}
if ( isLeft ) {
nodes [ parent ] -> left = nodes [ child ];
} else {
nodes [ parent ] -> right = nodes [ child ];
}
children . insert ( child );
}
for ( const auto & [ k , v ] : nodes ) {
if ( ! children . contains ( k )) {
return v ;
}
}
return nullptr ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func createBinaryTree ( descriptions [][] int ) * TreeNode {
nodes := map [ int ] * TreeNode {}
children := map [ int ] bool {}
for _ , d := range descriptions {
parent , child , isLeft := d [ 0 ], d [ 1 ], d [ 2 ]
if _ , ok := nodes [ parent ]; ! ok {
nodes [ parent ] = & TreeNode { Val : parent }
}
if _ , ok := nodes [ child ]; ! ok {
nodes [ child ] = & TreeNode { Val : child }
}
if isLeft == 1 {
nodes [ parent ]. Left = nodes [ child ]
} else {
nodes [ parent ]. Right = nodes [ child ]
}
children [ child ] = true
}
for k , v := range nodes {
if _ , ok := children [ k ]; ! ok {
return v
}
}
return nil
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 /**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function createBinaryTree ( descriptions : number [][]) : TreeNode | null {
const nodes : Record < number , TreeNode > = {};
const children = new Set < number > ();
for ( const [ parent , child , isLeft ] of descriptions ) {
if ( ! nodes [ parent ]) {
nodes [ parent ] = new TreeNode ( parent );
}
if ( ! nodes [ child ]) {
nodes [ child ] = new TreeNode ( child );
}
if ( isLeft ) {
nodes [ parent ]. left = nodes [ child ];
} else {
nodes [ parent ]. right = nodes [ child ];
}
children . add ( child );
}
for ( const [ k , v ] of Object . entries ( nodes )) {
if ( ! children . has ( + k )) {
return v ;
}
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58 // Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std :: cell :: RefCell ;
use std :: collections ::{ HashMap , HashSet };
use std :: rc :: Rc ;
impl Solution {
pub fn create_binary_tree ( descriptions : Vec < Vec < i32 >> ) -> Option < Rc < RefCell < TreeNode >>> {
let mut nodes = HashMap :: new ();
let mut children = HashSet :: new ();
for d in descriptions {
let parent = d [ 0 ];
let child = d [ 1 ];
let is_left = d [ 2 ];
nodes
. entry ( parent )
. or_insert_with ( || Rc :: new ( RefCell :: new ( TreeNode :: new ( parent ))));
nodes
. entry ( child )
. or_insert_with ( || Rc :: new ( RefCell :: new ( TreeNode :: new ( child ))));
if is_left == 1 {
nodes . get ( & parent ). unwrap (). borrow_mut (). left =
Some ( Rc :: clone ( nodes . get ( & child ). unwrap ()));
} else {
nodes . get ( & parent ). unwrap (). borrow_mut (). right =
Some ( Rc :: clone ( nodes . get ( & child ). unwrap ()));
}
children . insert ( child );
}
for ( key , node ) in & nodes {
if ! children . contains ( key ) {
return Some ( Rc :: clone ( node ));
}
}
None
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 /**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[][]} descriptions
* @return {TreeNode}
*/
var createBinaryTree = function ( descriptions ) {
const nodes = {};
const children = new Set ();
for ( const [ parent , child , isLeft ] of descriptions ) {
if ( ! nodes [ parent ]) {
nodes [ parent ] = new TreeNode ( parent );
}
if ( ! nodes [ child ]) {
nodes [ child ] = new TreeNode ( child );
}
if ( isLeft ) {
nodes [ parent ]. left = nodes [ child ];
} else {
nodes [ parent ]. right = nodes [ child ];
}
children . add ( child );
}
for ( const [ k , v ] of Object . entries ( nodes )) {
if ( ! children . has ( + k )) {
return v ;
}
}
};