二分查找
排序
数组
贪心
题目描述
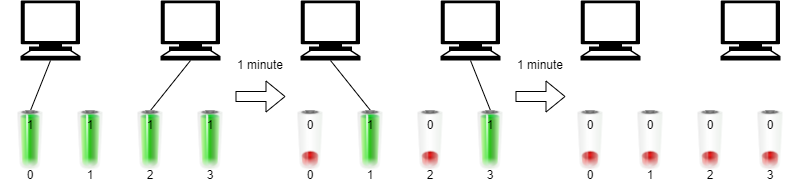
你有 n 台电脑。给你整数 n 和一个下标从 0 开始的整数数组 batteries ,其中第 i 个电池可以让一台电脑 运行 batteries[i] 分钟。你想使用这些电池让 全部 n 台电脑 同时 运行。
一开始,你可以给每台电脑连接 至多一个电池 。然后在任意整数时刻,你都可以将一台电脑与它的电池断开连接,并连接另一个电池,你可以进行这个操作 任意次 。新连接的电池可以是一个全新的电池,也可以是别的电脑用过的电池。断开连接和连接新的电池不会花费任何时间。
注意,你不能给电池充电。
请你返回你可以让 n 台电脑同时运行的 最长 分钟数。
示例 1:
输入: n = 2, batteries = [3,3,3]
输出: 4
解释:
一开始,将第一台电脑与电池 0 连接,第二台电脑与电池 1 连接。
2 分钟后,将第二台电脑与电池 1 断开连接,并连接电池 2 。注意,电池 0 还可以供电 1 分钟。
在第 3 分钟结尾,你需要将第一台电脑与电池 0 断开连接,然后连接电池 1 。
在第 4 分钟结尾,电池 1 也被耗尽,第一台电脑无法继续运行。
我们最多能同时让两台电脑同时运行 4 分钟,所以我们返回 4 。
示例 2:
输入: n = 2, batteries = [1,1,1,1]
输出: 2
解释:
一开始,将第一台电脑与电池 0 连接,第二台电脑与电池 2 连接。
一分钟后,电池 0 和电池 2 同时耗尽,所以你需要将它们断开连接,并将电池 1 和第一台电脑连接,电池 3 和第二台电脑连接。
1 分钟后,电池 1 和电池 3 也耗尽了,所以两台电脑都无法继续运行。
我们最多能让两台电脑同时运行 2 分钟,所以我们返回 2 。
提示:
1 <= n <= batteries.length <= 105 1 <= batteries[i] <= 109
解法
方法一:二分查找
我们注意到,如果我们可以让 \(n\) 台电脑同时运行 \(t\) 分钟,那么我们也可以让 \(n\) 台电脑同时运行 \(t' \le t\) 分钟,这存在着单调性。因此,我们可以使用二分查找的方法找到最大的 \(t\) 。
我们定义二分查找的左边界 \(l=0\) ,右边界 \(r=\sum_{i=0}^{n-1} batteries[i]\) 。每次二分查找的过程中,我们使用一个变量 \(mid\) 表示当前的中间值,即 \(mid = (l + r + 1) >> 1\) 。我们判断是否存在一种方案,使得 \(n\) 台电脑同时运行 \(mid\) 分钟。如果存在,那么我们就将 \(l\) 更新为 \(mid\) ,否则我们将 \(r\) 更新为 \(mid - 1\) 。最后,我们返回 \(l\) 即为答案。
问题转化为如何判断是否存在一种方案,使得 \(n\) 台电脑同时运行 \(mid\) 分钟。如果一个电池可以运行的分钟数大于 \(mid\) ,由于电脑同时运行 \(mid\) 分钟,而一个电池同一时间只能供电一台电脑,因此我们只能使用这个电池 \(mid\) 分钟。如果一个电池可以运行的分钟数小于等于 \(mid\) ,我们可以使用这个电池的全部电量。因此,我们统计所有电池可以供电的分钟数之和 \(s\) ,如果 \(s \ge n \times mid\) ,那么我们就可以使得 \(n\) 台电脑同时运行 \(mid\) 分钟。
时间复杂度 \(O(n \times \log M)\) ,其中 \(M\) 为所有电池的电量之和,空间复杂度 \(O(1)\) 。
Python3 Java C++ Go TypeScript Rust
class Solution :
def maxRunTime ( self , n : int , batteries : List [ int ]) -> int :
l , r = 0 , sum ( batteries )
while l < r :
mid = ( l + r + 1 ) >> 1
if sum ( min ( x , mid ) for x in batteries ) >= n * mid :
l = mid
else :
r = mid - 1
return l
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 class Solution {
public long maxRunTime ( int n , int [] batteries ) {
long l = 0 , r = 0 ;
for ( int x : batteries ) {
r += x ;
}
while ( l < r ) {
long mid = ( l + r + 1 ) >> 1 ;
long s = 0 ;
for ( int x : batteries ) {
s += Math . min ( mid , x );
}
if ( s >= n * mid ) {
l = mid ;
} else {
r = mid - 1 ;
}
}
return l ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 class Solution {
public :
long long maxRunTime ( int n , vector < int >& batteries ) {
long long l = 0 , r = 0 ;
for ( int x : batteries ) {
r += x ;
}
while ( l < r ) {
long long mid = ( l + r + 1 ) >> 1 ;
long long s = 0 ;
for ( int x : batteries ) {
s += min ( 1L L * x , mid );
}
if ( s >= n * mid ) {
l = mid ;
} else {
r = mid - 1 ;
}
}
return l ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 func maxRunTime ( n int , batteries [] int ) int64 {
l , r := 0 , 0
for _ , x := range batteries {
r += x
}
for l < r {
mid := ( l + r + 1 ) >> 1
s := 0
for _ , x := range batteries {
s += min ( x , mid )
}
if s >= n * mid {
l = mid
} else {
r = mid - 1
}
}
return int64 ( l )
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 function maxRunTime ( n : number , batteries : number []) : number {
let l = 0n ;
let r = 0n ;
for ( const x of batteries ) {
r += BigInt ( x );
}
while ( l < r ) {
const mid = ( l + r + 1n ) >> 1n ;
let s = 0n ;
for ( const x of batteries ) {
s += BigInt ( Math . min ( x , Number ( mid )));
}
if ( s >= mid * BigInt ( n )) {
l = mid ;
} else {
r = mid - 1n ;
}
}
return Number ( l );
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48 impl Solution {
#[allow(dead_code)]
pub fn max_run_time ( n : i32 , batteries : Vec < i32 > ) -> i64 {
// First sort the batteries
let mut batteries = batteries ;
let m = batteries . len () as i32 ;
batteries . sort ();
let mut extra_sum : i64 = 0 ;
for i in 0 .. ( m - n ) as usize {
extra_sum += batteries [ i ] as i64 ;
}
let mut i = ( m - n ) as usize ;
let mut cur_height = batteries [ i ];
let mut ret = cur_height as i64 ;
while extra_sum != 0 {
if i + 1 == ( m as usize ) {
assert! ( cur_height == * batteries . last (). unwrap ());
ret += extra_sum / ( n as i64 );
break ;
}
if batteries [ i ] == batteries [ i + 1 ] {
i += 1 ;
continue ;
}
let diff = extra_sum / (( i - (( m - n ) as usize ) + 1 ) as i64 );
if ( cur_height as i64 ) + diff <= ( batteries [ i + 1 ] as i64 ) {
ret = ( cur_height as i64 ) + diff ;
break ;
} else {
extra_sum -= (( batteries [ i + 1 ] - batteries [ i ]) as i64 )
* (( i - (( m - n ) as usize ) + 1 ) as i64 );
ret = batteries [ i + 1 ] as i64 ;
}
i += 1 ;
if i != ( m as usize ) {
cur_height = batteries [ i ];
}
}
ret
}
}
GitHub