2136. 全部开花的最早一天

题目描述

你有 n 枚花的种子。每枚种子必须先种下，才能开始生长、开花。播种需要时间，种子的生长也是如此。给你两个下标从 0 开始的整数数组 plantTime 和 growTime ，每个数组的长度都是 n ：

plantTime[i] 是播种第 i 枚种子所需的 完整天数 。每天，你只能为播种某一枚种子而劳作。无须连续几天都在种同一枚种子，但是种子播种必须在你工作的天数达到 plantTime[i] 之后才算完成。
growTime[i] 是第 i 枚种子完全种下后生长所需的 完整天数 。在它生长的最后一天之后，将会开花并且永远绽放。

从第 0 开始，你可以按任意顺序播种种子。

返回所有种子都开花的最早一天是第几天。

示例 1：

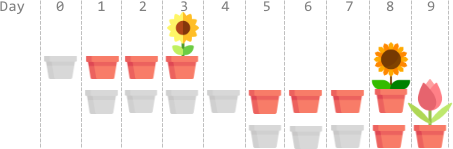
输入：plantTime = [1,4,3], growTime = [2,3,1]
输出：9
解释：灰色的花盆表示播种的日子，彩色的花盆表示生长的日子，花朵表示开花的日子。
一种最优方案是：
第 0 天，播种第 0 枚种子，种子生长 2 整天。并在第 3 天开花。
第 1、2、3、4 天，播种第 1 枚种子。种子生长 3 整天，并在第 8 天开花。
第 5、6、7 天，播种第 2 枚种子。种子生长 1 整天，并在第 9 天开花。
因此，在第 9 天，所有种子都开花。

示例 2：

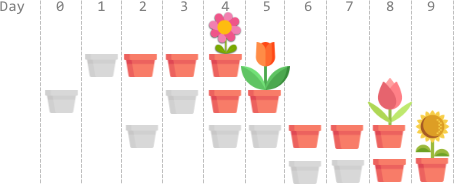
输入：plantTime = [1,2,3,2], growTime = [2,1,2,1]
输出：9
解释：灰色的花盆表示播种的日子，彩色的花盆表示生长的日子，花朵表示开花的日子。 
一种最优方案是：
第 1 天，播种第 0 枚种子，种子生长 2 整天。并在第 4 天开花。
第 0、3 天，播种第 1 枚种子。种子生长 1 整天，并在第 5 天开花。
第 2、4、5 天，播种第 2 枚种子。种子生长 2 整天，并在第 8 天开花。
第 6、7 天，播种第 3 枚种子。种子生长 1 整天，并在第 9 天开花。
因此，在第 9 天，所有种子都开花。

示例 3：

输入：plantTime = [1], growTime = [1]
输出：2
解释：第 0 天，播种第 0 枚种子。种子需要生长 1 整天，然后在第 2 天开花。
因此，在第 2 天，所有种子都开花。

提示：

n == plantTime.length == growTime.length
1 <= n <= 10⁵
1 <= plantTime[i], growTime[i] <= 10⁴

解法

方法一：贪心 + 排序

根据题目描述，我们知道，每一天只能为一枚种子进行播种，因此不管什么播种顺序，所有种子的播种时间之和总是等于 $\sum_{i=0}^{n-1} plantTime[i]$。那么，为了让尽快让所有种子开花，我们应该尽快播种生长时间最长的种子。因此，我们可以对所有种子按照生长时间从大到小进行排序，然后依次进行播种。

时间复杂度 $O(n \times \log n)$，空间复杂度 $O(n)$。其中 $n$ 是种子的数量。

Python3JavaC++GoTypeScriptRust

class Solution:
    def earliestFullBloom(self, plantTime: List[int], growTime: List[int]) -> int:
        ans = t = 0
        for pt, gt in sorted(zip(plantTime, growTime), key=lambda x: -x[1]):
            t += pt
            ans = max(ans, t + gt)
        return ans

class Solution {
    public int earliestFullBloom(int[] plantTime, int[] growTime) {
        int n = plantTime.length;
        Integer[] idx = new Integer[n];
        for (int i = 0; i < n; i++) {
            idx[i] = i;
        }
        Arrays.sort(idx, (i, j) -> growTime[j] - growTime[i]);
        int ans = 0, t = 0;
        for (int i : idx) {
            t += plantTime[i];
            ans = Math.max(ans, t + growTime[i]);
        }
        return ans;
    }
}

class Solution {
public:
    int earliestFullBloom(vector<int>& plantTime, vector<int>& growTime) {
        int n = plantTime.size();
        vector<int> idx(n);
        iota(idx.begin(), idx.end(), 0);
        sort(idx.begin(), idx.end(), [&](int i, int j) { return growTime[j] < growTime[i]; });
        int ans = 0, t = 0;
        for (int i : idx) {
            t += plantTime[i];
            ans = max(ans, t + growTime[i]);
        }
        return ans;
    }
};

func earliestFullBloom(plantTime []int, growTime []int) (ans int) {
    n := len(plantTime)
    idx := make([]int, n)
    for i := range idx {
        idx[i] = i
    }
    sort.Slice(idx, func(i, j int) bool { return growTime[idx[j]] < growTime[idx[i]] })
    t := 0
    for _, i := range idx {
        t += plantTime[i]
        ans = max(ans, t+growTime[i])
    }
    return
}

function earliestFullBloom(plantTime: number[], growTime: number[]): number {
    const n = plantTime.length;
    const idx: number[] = Array.from({ length: n }, (_, i) => i);
    idx.sort((i, j) => growTime[j] - growTime[i]);
    let [ans, t] = [0, 0];
    for (const i of idx) {
        t += plantTime[i];
        ans = Math.max(ans, t + growTime[i]);
    }
    return ans;
}

impl Solution {
    pub fn earliest_full_bloom(plant_time: Vec<i32>, grow_time: Vec<i32>) -> i32 {
        let mut idx: Vec<usize> = (0..plant_time.len()).collect();
        idx.sort_by_key(|&i| -&grow_time[i]);
        let mut ans = 0;
        let mut t = 0;
        for &i in &idx {
            t += plant_time[i];
            ans = ans.max(t + grow_time[i]);
        }
        ans
    }
}

2136. 全部开花的最早一天

题目描述

解法

方法一：贪心 + 排序

评论