贪心
数组
矩阵
前缀和
题目描述
给你一个 m x n 的二进制矩阵 grid ,每个格子要么为 0 (空)要么为 1 (被占据)。
给你邮票的尺寸为 stampHeight x stampWidth 。我们想将邮票贴进二进制矩阵中,且满足以下 限制 和 要求 :
覆盖所有 空 格子。
不覆盖任何 被占据 的格子。
我们可以放入任意数目的邮票。
邮票可以相互有 重叠 部分。
邮票不允许 旋转 。
邮票必须完全在矩阵 内 。
如果在满足上述要求的前提下,可以放入邮票,请返回 true ,否则返回 false 。
示例 1:
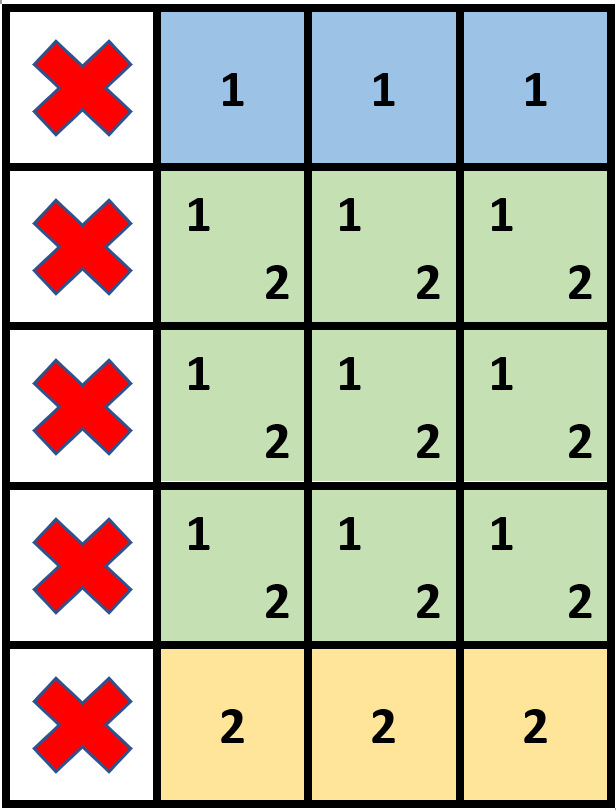
输入: grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3
输出: true
解释: 我们放入两个有重叠部分的邮票(图中标号为 1 和 2),它们能覆盖所有与空格子。
示例 2:
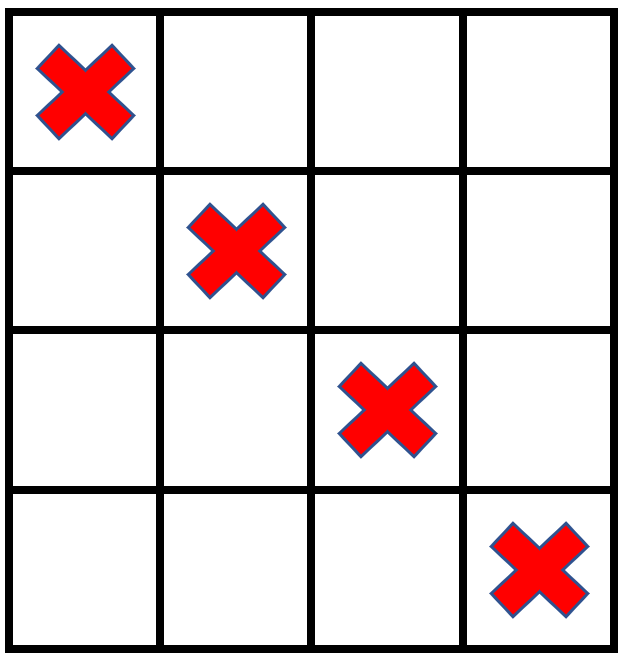
输入: grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2
输出: false
解释: 没办法放入邮票覆盖所有的空格子,且邮票不超出网格图以外。
提示:
m == grid.lengthn == grid[r].length1 <= m, n <= 105 1 <= m * n <= 2 * 105 grid[r][c] 要么是 0 ,要么是 1 。1 <= stampHeight, stampWidth <= 105
解法
方法一:二维前缀和 + 二维差分
根据题目描述,每一个空格子都必须被邮票覆盖,而且不能覆盖任何被占据的格子。因此,我们可以遍历二维矩阵,对于每个格子,如果以该格子为左上角的 $stampHeight \times stampWidth$ 的区域内的所有格子都是空格子(即没有被占据),那么我们就可以在该格子处放置一个邮票。
为了快速判断一个区域内的所有格子是否都是空格子,我们可以使用二维前缀和。我们用 $s_{i,j}$ 表示二维矩阵中从 $(1,1)$ 到 $(i,j)$ 的子矩阵中被占据的格子的数量。即 $s_{i, j} = s_{i - 1, j} + s_{i, j - 1} - s_{i - 1, j - 1} + grid_{i-1, j-1}$。
那么以 $(i, j)$ 为左上角,且高度和宽度分别为 $stampHeight$ 和 $stampWidth$ 的子矩阵的右下角坐标为 $(x, y) = (i + stampHeight - 1, j + stampWidth - 1)$,我们可以通过 $s_{x, y} - s_{x, j - 1} - s_{i - 1, y} + s_{i - 1, j - 1}$ 来计算出该子矩阵中被占据的格子的数量。如果该子矩阵中被占据的格子的数量为 $0$,那么我们就可以在 $(i, j)$ 处放置一个邮票,放置邮票后,这 $stampHeight \times stampWidth$ 的区域内的所有格子都会变成被占据的格子,我们可以用二维差分数组 $d$ 来记录这一变化。即:
$$
\begin{aligned}
d_{i, j} &\leftarrow d_{i, j} + 1 \
d_{i, y + 1} &\leftarrow d_{i, y + 1} - 1 \
d_{x + 1, j} &\leftarrow d_{x + 1, j} - 1 \
d_{x + 1, y + 1} &\leftarrow d_{x + 1, y + 1} + 1
\end{aligned}
$$
最后,我们对二维差分数组 $d$ 进行前缀和运算,可以得出每个格子被邮票覆盖的次数。如果某个格子没有被占据,且被邮票覆盖的次数为 $0$,那么我们就无法将邮票放置在该格子处,因此我们需要返回 $\texttt{false}$。如果所有“没被占据的格子”都成功被邮票覆盖,返回 $\texttt{true}$。
时间复杂度 $O(m \times n)$,空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别是二维矩阵的高度和宽度。
Python3 Java C++ Go TypeScript Rust JavaScript Kotlin
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 class Solution :
def possibleToStamp (
self , grid : List [ List [ int ]], stampHeight : int , stampWidth : int
) -> bool :
m , n = len ( grid ), len ( grid [ 0 ])
s = [[ 0 ] * ( n + 1 ) for _ in range ( m + 1 )]
for i , row in enumerate ( grid , 1 ):
for j , v in enumerate ( row , 1 ):
s [ i ][ j ] = s [ i - 1 ][ j ] + s [ i ][ j - 1 ] - s [ i - 1 ][ j - 1 ] + v
d = [[ 0 ] * ( n + 2 ) for _ in range ( m + 2 )]
for i in range ( 1 , m - stampHeight + 2 ):
for j in range ( 1 , n - stampWidth + 2 ):
x , y = i + stampHeight - 1 , j + stampWidth - 1
if s [ x ][ y ] - s [ x ][ j - 1 ] - s [ i - 1 ][ y ] + s [ i - 1 ][ j - 1 ] == 0 :
d [ i ][ j ] += 1
d [ i ][ y + 1 ] -= 1
d [ x + 1 ][ j ] -= 1
d [ x + 1 ][ y + 1 ] += 1
for i , row in enumerate ( grid , 1 ):
for j , v in enumerate ( row , 1 ):
d [ i ][ j ] += d [ i - 1 ][ j ] + d [ i ][ j - 1 ] - d [ i - 1 ][ j - 1 ]
if v == 0 and d [ i ][ j ] == 0 :
return False
return True
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 class Solution {
public boolean possibleToStamp ( int [][] grid , int stampHeight , int stampWidth ) {
int m = grid . length , n = grid [ 0 ] . length ;
int [][] s = new int [ m + 1 ][ n + 1 ] ;
for ( int i = 1 ; i <= m ; ++ i ) {
for ( int j = 1 ; j <= n ; ++ j ) {
s [ i ][ j ] = s [ i - 1 ][ j ] + s [ i ][ j - 1 ] - s [ i - 1 ][ j - 1 ] + grid [ i - 1 ][ j - 1 ] ;
}
}
int [][] d = new int [ m + 2 ][ n + 2 ] ;
for ( int i = 1 ; i + stampHeight - 1 <= m ; ++ i ) {
for ( int j = 1 ; j + stampWidth - 1 <= n ; ++ j ) {
int x = i + stampHeight - 1 , y = j + stampWidth - 1 ;
if ( s [ x ][ y ] - s [ x ][ j - 1 ] - s [ i - 1 ][ y ] + s [ i - 1 ][ j - 1 ] == 0 ) {
d [ i ][ j ]++ ;
d [ i ][ y + 1 ]-- ;
d [ x + 1 ][ j ]-- ;
d [ x + 1 ][ y + 1 ]++ ;
}
}
}
for ( int i = 1 ; i <= m ; ++ i ) {
for ( int j = 1 ; j <= n ; ++ j ) {
d [ i ][ j ] += d [ i - 1 ][ j ] + d [ i ][ j - 1 ] - d [ i - 1 ][ j - 1 ] ;
if ( grid [ i - 1 ][ j - 1 ] == 0 && d [ i ][ j ] == 0 ) {
return false ;
}
}
}
return true ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 class Solution {
public :
bool possibleToStamp ( vector < vector < int >>& grid , int stampHeight , int stampWidth ) {
int m = grid . size (), n = grid [ 0 ]. size ();
vector < vector < int >> s ( m + 1 , vector < int > ( n + 1 ));
for ( int i = 1 ; i <= m ; ++ i ) {
for ( int j = 1 ; j <= n ; ++ j ) {
s [ i ][ j ] = s [ i - 1 ][ j ] + s [ i ][ j - 1 ] - s [ i - 1 ][ j - 1 ] + grid [ i - 1 ][ j - 1 ];
}
}
vector < vector < int >> d ( m + 2 , vector < int > ( n + 2 ));
for ( int i = 1 ; i + stampHeight - 1 <= m ; ++ i ) {
for ( int j = 1 ; j + stampWidth - 1 <= n ; ++ j ) {
int x = i + stampHeight - 1 , y = j + stampWidth - 1 ;
if ( s [ x ][ y ] - s [ x ][ j - 1 ] - s [ i - 1 ][ y ] + s [ i - 1 ][ j - 1 ] == 0 ) {
d [ i ][ j ] ++ ;
d [ i ][ y + 1 ] -- ;
d [ x + 1 ][ j ] -- ;
d [ x + 1 ][ y + 1 ] ++ ;
}
}
}
for ( int i = 1 ; i <= m ; ++ i ) {
for ( int j = 1 ; j <= n ; ++ j ) {
d [ i ][ j ] += d [ i - 1 ][ j ] + d [ i ][ j - 1 ] - d [ i - 1 ][ j - 1 ];
if ( grid [ i - 1 ][ j - 1 ] == 0 && d [ i ][ j ] == 0 ) {
return false ;
}
}
}
return true ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 func possibleToStamp ( grid [][] int , stampHeight int , stampWidth int ) bool {
m , n := len ( grid ), len ( grid [ 0 ])
s := make ([][] int , m + 1 )
for i := range s {
s [ i ] = make ([] int , n + 1 )
}
for i := 1 ; i <= m ; i ++ {
for j := 1 ; j <= n ; j ++ {
s [ i ][ j ] = s [ i - 1 ][ j ] + s [ i ][ j - 1 ] - s [ i - 1 ][ j - 1 ] + grid [ i - 1 ][ j - 1 ]
}
}
d := make ([][] int , m + 2 )
for i := range d {
d [ i ] = make ([] int , n + 2 )
}
for i := 1 ; i + stampHeight - 1 <= m ; i ++ {
for j := 1 ; j + stampWidth - 1 <= n ; j ++ {
x , y := i + stampHeight - 1 , j + stampWidth - 1
if s [ x ][ y ] - s [ x ][ j - 1 ] - s [ i - 1 ][ y ] + s [ i - 1 ][ j - 1 ] == 0 {
d [ i ][ j ] ++
d [ i ][ y + 1 ] --
d [ x + 1 ][ j ] --
d [ x + 1 ][ y + 1 ] ++
}
}
}
for i := 1 ; i <= m ; i ++ {
for j := 1 ; j <= n ; j ++ {
d [ i ][ j ] += d [ i - 1 ][ j ] + d [ i ][ j - 1 ] - d [ i - 1 ][ j - 1 ]
if grid [ i - 1 ][ j - 1 ] == 0 && d [ i ][ j ] == 0 {
return false
}
}
}
return true
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 function possibleToStamp ( grid : number [][], stampHeight : number , stampWidth : number ) : boolean {
const m = grid . length ;
const n = grid [ 0 ]. length ;
const s : number [][] = Array . from ({ length : m + 1 }, () => Array ( n + 1 ). fill ( 0 ));
for ( let i = 1 ; i <= m ; ++ i ) {
for ( let j = 1 ; j <= n ; ++ j ) {
s [ i ][ j ] = s [ i - 1 ][ j ] + s [ i ][ j - 1 ] - s [ i - 1 ][ j - 1 ] + grid [ i - 1 ][ j - 1 ];
}
}
const d : number [][] = Array . from ({ length : m + 2 }, () => Array ( n + 2 ). fill ( 0 ));
for ( let i = 1 ; i + stampHeight - 1 <= m ; ++ i ) {
for ( let j = 1 ; j + stampWidth - 1 <= n ; ++ j ) {
const [ x , y ] = [ i + stampHeight - 1 , j + stampWidth - 1 ];
if ( s [ x ][ y ] - s [ x ][ j - 1 ] - s [ i - 1 ][ y ] + s [ i - 1 ][ j - 1 ] === 0 ) {
d [ i ][ j ] ++ ;
d [ i ][ y + 1 ] -- ;
d [ x + 1 ][ j ] -- ;
d [ x + 1 ][ y + 1 ] ++ ;
}
}
}
for ( let i = 1 ; i <= m ; ++ i ) {
for ( let j = 1 ; j <= n ; ++ j ) {
d [ i ][ j ] += d [ i - 1 ][ j ] + d [ i ][ j - 1 ] - d [ i - 1 ][ j - 1 ];
if ( grid [ i - 1 ][ j - 1 ] === 0 && d [ i ][ j ] === 0 ) {
return false ;
}
}
}
return true ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65 impl Solution {
pub fn possible_to_stamp ( grid : Vec < Vec < i32 >> , stamp_height : i32 , stamp_width : i32 ) -> bool {
let n : usize = grid . len ();
let m : usize = grid [ 0 ]. len ();
let mut prefix_vec : Vec < Vec < i32 >> = vec! [ vec! [ 0 ; m + 1 ]; n + 1 ];
// Initialize the prefix vector
for i in 0 .. n {
for j in 0 .. m {
prefix_vec [ i + 1 ][ j + 1 ] =
prefix_vec [ i ][ j + 1 ] + prefix_vec [ i + 1 ][ j ] - prefix_vec [ i ][ j ] + grid [ i ][ j ];
}
}
let mut diff_vec : Vec < Vec < i32 >> = vec! [ vec! [ 0 ; m + 1 ]; n + 1 ];
// Construct the difference vector based on prefix sum vector
for i in 0 .. n {
for j in 0 .. m {
// If the value of the cell is one, just bypass this
if grid [ i ][ j ] == 1 {
continue ;
}
// Otherwise, try stick the stamp
let x : usize = i + ( stamp_height as usize );
let y : usize = j + ( stamp_width as usize );
// Check the bound
if x <= n && y <= m {
// If the region can be sticked (All cells are empty, which means the sum will be zero)
if prefix_vec [ x ][ y ] - prefix_vec [ x ][ j ] - prefix_vec [ i ][ y ] + prefix_vec [ i ][ j ]
== 0
{
// Update the difference vector
diff_vec [ i ][ j ] += 1 ;
diff_vec [ x ][ y ] += 1 ;
diff_vec [ x ][ j ] -= 1 ;
diff_vec [ i ][ y ] -= 1 ;
}
}
}
}
let mut check_vec : Vec < Vec < i32 >> = vec! [ vec! [ 0 ; m + 1 ]; n + 1 ];
// Check the prefix sum of difference vector, to determine if there is any empty cell left
for i in 0 .. n {
for j in 0 .. m {
// If the value of the cell is one, just bypass this
if grid [ i ][ j ] == 1 {
continue ;
}
// Otherwise, check if the region is empty, by calculating the prefix sum of difference vector
check_vec [ i + 1 ][ j + 1 ] =
check_vec [ i ][ j + 1 ] + check_vec [ i + 1 ][ j ] - check_vec [ i ][ j ] + diff_vec [ i ][ j ];
if check_vec [ i + 1 ][ j + 1 ] == 0 {
return false ;
}
}
}
true
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 /**
* @param {number[][]} grid
* @param {number} stampHeight
* @param {number} stampWidth
* @return {boolean}
*/
var possibleToStamp = function ( grid , stampHeight , stampWidth ) {
const m = grid . length ;
const n = grid [ 0 ]. length ;
const s = Array . from ({ length : m + 1 }, () => Array ( n + 1 ). fill ( 0 ));
for ( let i = 1 ; i <= m ; ++ i ) {
for ( let j = 1 ; j <= n ; ++ j ) {
s [ i ][ j ] = s [ i - 1 ][ j ] + s [ i ][ j - 1 ] - s [ i - 1 ][ j - 1 ] + grid [ i - 1 ][ j - 1 ];
}
}
const d = Array . from ({ length : m + 2 }, () => Array ( n + 2 ). fill ( 0 ));
for ( let i = 1 ; i + stampHeight - 1 <= m ; ++ i ) {
for ( let j = 1 ; j + stampWidth - 1 <= n ; ++ j ) {
const [ x , y ] = [ i + stampHeight - 1 , j + stampWidth - 1 ];
if ( s [ x ][ y ] - s [ x ][ j - 1 ] - s [ i - 1 ][ y ] + s [ i - 1 ][ j - 1 ] === 0 ) {
d [ i ][ j ] ++ ;
d [ i ][ y + 1 ] -- ;
d [ x + 1 ][ j ] -- ;
d [ x + 1 ][ y + 1 ] ++ ;
}
}
}
for ( let i = 1 ; i <= m ; ++ i ) {
for ( let j = 1 ; j <= n ; ++ j ) {
d [ i ][ j ] += d [ i - 1 ][ j ] + d [ i ][ j - 1 ] - d [ i - 1 ][ j - 1 ];
if ( grid [ i - 1 ][ j - 1 ] === 0 && d [ i ][ j ] === 0 ) {
return false ;
}
}
}
return true ;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69 class Solution {
fun possibleToStamp ( grid : Array < IntArray > , stampHeight : Int , stampWidth : Int ): Boolean {
val m = grid . size
val n = grid [ 0 ] . size
var prefix_sums_matrix = Array ( m + 1 ) { IntArray ( n + 1 ) }
var diff_matrix = Array ( m + 1 ) { IntArray ( n + 1 ) }
var sum_matrix = Array ( m + 1 ) { IntArray ( n + 1 ) }
for ( i in 0. . < m ) {
for ( j in 0. . < n ) {
prefix_sums_matrix [ i + 1 ][ j + 1 ] =
prefix_sums_matrix [ i + 1 ][ j ] +
prefix_sums_matrix [ i ][ j + 1 ] -
prefix_sums_matrix [ i ][ j ] +
grid [ i ][ j ]
}
}
for ( i in 0. . < m ) {
for ( j in 0. . < n ) {
if ( grid [ i ][ j ] != 0 ) {
continue
}
val bottom = i + stampHeight
val right = j + stampWidth
if ( bottom > m || right > n ) {
continue
}
val sum = prefix_sums_matrix [ bottom ][ right ] -
prefix_sums_matrix [ bottom ][ j ] -
prefix_sums_matrix [ i ][ right ] +
prefix_sums_matrix [ i ][ j ]
if ( sum == 0 ) {
diff_matrix [ i ][ j ] += 1
diff_matrix [ bottom ][ right ] += 1
diff_matrix [ i ][ right ] -= 1
diff_matrix [ bottom ][ j ] -= 1
}
}
}
for ( i in 0. . < m ) {
for ( j in 0. . < n ) {
if ( grid [ i ][ j ] != 0 ) {
continue
}
val sum = sum_matrix [ i ][ j + 1 ] +
sum_matrix [ i + 1 ][ j ] -
sum_matrix [ i ][ j ] +
diff_matrix [ i ][ j ]
if ( sum == 0 ) {
return false
}
sum_matrix [ i + 1 ][ j + 1 ] = sum
}
}
return true
}
}