跳转至

2106. 摘水果

题目描述

在一个无限的 x 坐标轴上，有许多水果分布在其中某些位置。给你一个二维整数数组 fruits ，其中 fruits[i] = [positioni, amounti] 表示共有 amounti 个水果放置在 positioni 上。fruits 已经按 positioni 升序排列 ，每个 positioni 互不相同 。

另给你两个整数 startPos 和 k 。最初，你位于 startPos 。从任何位置，你可以选择 向左或者向右 走。在 x 轴上每移动 一个单位 ，就记作 一步 。你总共可以走 最多 k 步。你每达到一个位置，都会摘掉全部的水果，水果也将从该位置消失（不会再生）。

返回你可以摘到水果的 最大总数 。

 

示例 1：

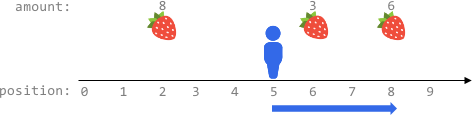
输入：fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4
输出：9
解释：
最佳路线为：
- 向右移动到位置 6 ，摘到 3 个水果
- 向右移动到位置 8 ，摘到 6 个水果
移动 3 步，共摘到 3 + 6 = 9 个水果

示例 2：

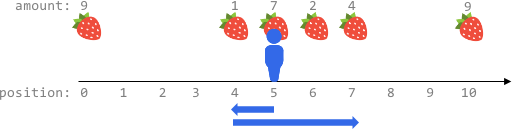
输入：fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4
输出：14
解释：
可以移动最多 k = 4 步，所以无法到达位置 0 和位置 10 。
最佳路线为：
- 在初始位置 5 ，摘到 7 个水果
- 向左移动到位置 4 ，摘到 1 个水果
- 向右移动到位置 6 ，摘到 2 个水果
- 向右移动到位置 7 ，摘到 4 个水果
移动 1 + 3 = 4 步，共摘到 7 + 1 + 2 + 4 = 14 个水果

示例 3：

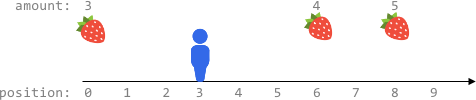
输入：fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2
输出：0
解释：
最多可以移动 k = 2 步，无法到达任一有水果的地方

 

提示：

  • 1 <= fruits.length <= 105
  • fruits[i].length == 2
  • 0 <= startPos, positioni <= 2 * 105
  • 对于任意 i > 0 ，positioni-1 < positioni 均成立（下标从 0 开始计数）
  • 1 <= amounti <= 104
  • 0 <= k <= 2 * 105

解法

方法一：双指针

我们不妨假设移动的位置区间为 $[l,r]$，开始位置为 $startPos$，来看看如何算出移动的最小步数。根据 $startPos$ 所处的位置，我们可以分为三种情况：

  1. 如果 $startPos \leq l$，那么就是从 $startPos$ 一直向右移动到 $r$。移动的最小步数为 $r - startPos$；
  2. 如果 $startPos \geq r$，那么就是从 $startPos$ 一直向左移动到 $l$。移动的最小步数为 $startPos - l$；
  3. 如果 $l \lt startPos \lt r$，那么可以从 $startPos$ 向左移动到 $l$，再向右移动到 $r$；也可以从 $startPos$ 向右移动到 $r$，再向左移动到 $l$。移动的最小步数为 $r - l + \min(\lvert startPos - l \rvert, \lvert r - startPos \rvert)$。

以上三种情况可以统一用式子 $r - l + \min(\lvert startPos - l \rvert, \lvert r - startPos \rvert)$ 表示。

假设我们固定区间右端点 $r$，向右移动左端点 $l$，我们来看看最小移动步数是怎么变化的。

  1. 如果 $startPos \leq l$，随着 $l$ 的增大，最小步数不会发生变化。
  2. 如果 $startPos \gt l$，随着 $l$ 的增大，最小步数会减小。

因此，随着 $l$ 的增大，最小移动步数一定是非严格单调递减的。基于此，我们可以使用双指针的方法，找出所有符合条件的最大区间，然后取所有符合条件的区间中水果总数最大的一个作为答案。

具体地，我们用两个指针 $i$ 和 $j$ 分别指向区间的左右下标，初始时 $i = j = 0$。另外用一个变量 $s$ 记录区间内的水果总数，初始时 $s = 0$。

每次我们将 $j$ 加入区间中，然后更新 $s = s + fruits[j][1]$。如果此时区间内的最小步数 $fruits[j][0] - fruits[i][0] + \min(\lvert startPos - fruits[i][0] \rvert, \lvert startPos - fruits[j][0] \rvert)$ 大于 $k$，那么我们就将 $i$ 循环向右移动，直到 $i \gt j$ 或者区间内的最小步数小于等于 $k$。此时我们更新答案 $ans = \max(ans, s)$。继续移动 $j$，直到 $j$ 到达数组末尾。

最后返回答案即可。

时间复杂度 $O(n)$，其中 $n$ 是数组的长度。空间复杂度 $O(1)$。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution:
    def maxTotalFruits(self, fruits: List[List[int]], startPos: int, k: int) -> int:
        ans = i = s = 0
        for j, (pj, fj) in enumerate(fruits):
            s += fj
            while (
                i <= j
                and pj
                - fruits[i][0]
                + min(abs(startPos - fruits[i][0]), abs(startPos - fruits[j][0]))
                > k
            ):
                s -= fruits[i][1]
                i += 1
            ans = max(ans, s)
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution {
    public int maxTotalFruits(int[][] fruits, int startPos, int k) {
        int ans = 0, s = 0;
        for (int i = 0, j = 0; j < fruits.length; ++j) {
            int pj = fruits[j][0], fj = fruits[j][1];
            s += fj;
            while (i <= j
                && pj - fruits[i][0]
                        + Math.min(Math.abs(startPos - fruits[i][0]), Math.abs(startPos - pj))
                    > k) {
                s -= fruits[i++][1];
            }
            ans = Math.max(ans, s);
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution {
public:
    int maxTotalFruits(vector<vector<int>>& fruits, int startPos, int k) {
        int ans = 0, s = 0;
        for (int i = 0, j = 0; j < fruits.size(); ++j) {
            int pj = fruits[j][0], fj = fruits[j][1];
            s += fj;
            while (i <= j && pj - fruits[i][0] + min(abs(startPos - fruits[i][0]), abs(startPos - pj)) > k) {
                s -= fruits[i++][1];
            }
            ans = max(ans, s);
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
func maxTotalFruits(fruits [][]int, startPos int, k int) (ans int) {
    var s, i int
    for j, f := range fruits {
        s += f[1]
        for i <= j && f[0]-fruits[i][0]+min(abs(startPos-fruits[i][0]), abs(startPos-f[0])) > k {
            s -= fruits[i][1]
            i += 1
        }
        ans = max(ans, s)
    }
    return
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
function maxTotalFruits(fruits: number[][], startPos: number, k: number): number {
    let ans = 0;
    let s = 0;
    for (let i = 0, j = 0; j < fruits.length; ++j) {
        const [pj, fj] = fruits[j];
        s += fj;
        while (
            i <= j &&
            pj -
                fruits[i][0] +
                Math.min(Math.abs(startPos - fruits[i][0]), Math.abs(startPos - pj)) >
                k
        ) {
            s -= fruits[i++][1];
        }
        ans = Math.max(ans, s);
    }
    return ans;
}

评论