2090. 半径为 k 的子数组平均值

题目描述

给你一个下标从 0 开始的数组 nums ，数组中有 n 个整数，另给你一个整数 k 。

半径为 k 的子数组平均值 是指：nums 中一个以下标 i 为中心且半径为 k 的子数组中所有元素的平均值，即下标在 i - k 和 i + k 范围（含 i - k 和 i + k）内所有元素的平均值。如果在下标 i 前或后不足 k 个元素，那么 半径为 k 的子数组平均值 是 -1 。

构建并返回一个长度为 n 的数组 avgs ，其中 avgs[i] 是以下标 i 为中心的子数组的 半径为 k 的子数组平均值 。

x 个元素的 平均值 是 x 个元素相加之和除以 x ，此时使用截断式 整数除法 ，即需要去掉结果的小数部分。

例如，四个元素 2、3、1 和 5 的平均值是 (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75，截断后得到 2 。

示例 1：

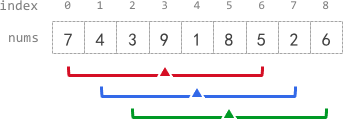
输入：nums = [7,4,3,9,1,8,5,2,6], k = 3
输出：[-1,-1,-1,5,4,4,-1,-1,-1]
解释：
- avg[0]、avg[1] 和 avg[2] 是 -1 ，因为在这几个下标前的元素数量都不足 k 个。
- 中心为下标 3 且半径为 3 的子数组的元素总和是：7 + 4 + 3 + 9 + 1 + 8 + 5 = 37 。
  使用截断式 整数除法，avg[3] = 37 / 7 = 5 。
- 中心为下标 4 的子数组，avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4 。
- 中心为下标 5 的子数组，avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4 。
- avg[6]、avg[7] 和 avg[8] 是 -1 ，因为在这几个下标后的元素数量都不足 k 个。

示例 2：

输入：nums = [100000], k = 0
输出：[100000]
解释：
- 中心为下标 0 且半径 0 的子数组的元素总和是：100000 。
  avg[0] = 100000 / 1 = 100000 。

示例 3：

输入：nums = [8], k = 100000
输出：[-1]
解释：
- avg[0] 是 -1 ，因为在下标 0 前后的元素数量均不足 k 。

提示：

n == nums.length
1 <= n <= 10⁵
0 <= nums[i], k <= 10⁵

解法

方法一：滑动窗口

半径为 $k$ 的子数组的长度为 $k \times 2 + 1$，因此我们可以维护一个大小为 $k \times 2 + 1$ 的窗口，记窗口中的所有元素和为 $s$。

我们创建一个长度为 $n$ 的答案数组 $\textit{ans}$，初始时每个元素都为 $-1$。

接下来，我们遍历数组 $\textit{nums}$，将 $\textit{nums}[i]$ 的值加到窗口的和 $s$ 中，如果此时 $i \geq k \times 2$，说明此时窗口大小为 $k \times 2 + 1$，那么 $\textit{ans}[i-k] = \frac{s}{k \times 2 + 1}$，然后我们将 $\textit{nums}[i - k \times 2]$ 的值从窗口和 $s$ 中移出。继续遍历下个元素。

最后返回答案数组即可。

时间复杂度 $O(n)$，其中 $n$ 为数组 $\textit{nums}$ 的长度。忽略答案数组的空间消耗，空间复杂度 $O(1)$。

Python3JavaC++GoTypeScript

class Solution:
    def getAverages(self, nums: List[int], k: int) -> List[int]:
        n = len(nums)
        ans = [-1] * n
        s = 0
        for i, x in enumerate(nums):
            s += x
            if i >= k * 2:
                ans[i - k] = s // (k * 2 + 1)
                s -= nums[i - k * 2]
        return ans

class Solution {
    public int[] getAverages(int[] nums, int k) {
        int n = nums.length;
        int[] ans = new int[n];
        Arrays.fill(ans, -1);
        long s = 0;
        for (int i = 0; i < n; ++i) {
            s += nums[i];
            if (i >= k * 2) {
                ans[i - k] = (int) (s / (k * 2 + 1));
                s -= nums[i - k * 2];
            }
        }
        return ans;
    }
}

class Solution {
public:
    vector<int> getAverages(vector<int>& nums, int k) {
        int n = nums.size();
        vector<int> ans(n, -1);
        long long s = 0;
        for (int i = 0; i < n; ++i) {
            s += nums[i];
            if (i >= k * 2) {
                ans[i - k] = s / (k * 2 + 1);
                s -= nums[i - k * 2];
            }
        }
        return ans;
    }
};

func getAverages(nums []int, k int) []int {
    ans := make([]int, len(nums))
    for i := range ans {
        ans[i] = -1
    }
    s := 0
    for i, x := range nums {
        s += x
        if i >= k*2 {
            ans[i-k] = s / (k*2 + 1)
            s -= nums[i-k*2]
        }
    }
    return ans
}

function getAverages(nums: number[], k: number): number[] {
    const n = nums.length;
    const ans: number[] = Array(n).fill(-1);
    let s = 0;
    for (let i = 0; i < n; ++i) {
        s += nums[i];
        if (i >= k * 2) {
            ans[i - k] = Math.floor(s / (k * 2 + 1));
            s -= nums[i - k * 2];
        }
    }
    return ans;
}

2090. 半径为 k 的子数组平均值

题目描述

解法

方法一：滑动窗口

评论