


题目描述
有一个 8 x 8 的棋盘,它包含 n 个棋子(棋子包括车,后和象三种)。给你一个长度为 n 的字符串数组 pieces ,其中 pieces[i] 表示第 i 个棋子的类型(车,后或象)。除此以外,还给你一个长度为 n 的二维整数数组 positions ,其中 positions[i] = [ri, ci] 表示第 i 个棋子现在在棋盘上的位置为 (ri, ci) ,棋盘下标从 1 开始。
每个棋子的移动中,首先选择移动的 方向 ,然后选择 移动的步数 ,同时你要确保移动过程中棋子不能移到棋盘以外的地方。棋子需按照以下规则移动:
- 车可以 水平或者竖直 从
(r, c) 沿着方向 (r+1, c),(r-1, c),(r, c+1) 或者 (r, c-1) 移动。
- 后可以 水平竖直或者斜对角 从
(r, c) 沿着方向 (r+1, c),(r-1, c),(r, c+1),(r, c-1),(r+1, c+1),(r+1, c-1),(r-1, c+1),(r-1, c-1) 移动。
- 象可以 斜对角 从
(r, c) 沿着方向 (r+1, c+1),(r+1, c-1),(r-1, c+1),(r-1, c-1) 移动。
你必须同时 移动 棋盘上的每一个棋子。移动组合 包含所有棋子的 移动 。每一秒,每个棋子都沿着它们选择的方向往前移动 一步 ,直到它们到达目标位置。所有棋子从时刻 0 开始移动。如果在某个时刻,两个或者更多棋子占据了同一个格子,那么这个移动组合 不有效 。
请你返回 有效 移动组合的数目。
注意:
- 初始时,不会有两个棋子 在 同一个位置 。
- 有可能在一个移动组合中,有棋子不移动。
- 如果两个棋子 直接相邻 且两个棋子下一秒要互相占据对方的位置,可以将它们在同一秒内 交换位置 。
示例 1:
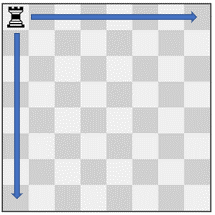
输入:pieces = ["rook"], positions = [[1,1]]
输出:15
解释:上图展示了棋子所有可能的移动。
示例 2:
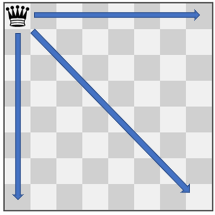
输入:pieces = ["queen"], positions = [[1,1]]
输出:22
解释:上图展示了棋子所有可能的移动。
示例 3:
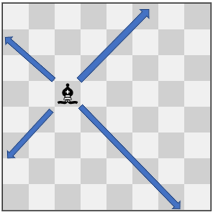
输入:pieces = ["bishop"], positions = [[4,3]]
输出:12
解释:上图展示了棋子所有可能的移动。
示例 4:
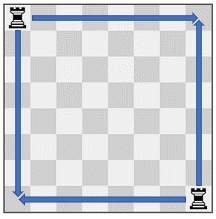
输入:pieces = ["rook","rook"], positions = [[1,1],[8,8]]
输出:223
解释:每个车有 15 种移动,所以总共有 15 * 15 = 225 种移动组合。
但是,有两个是不有效的移动组合:
- 将两个车都移动到 (8, 1) ,会导致它们在同一个格子相遇。
- 将两个车都移动到 (1, 8) ,会导致它们在同一个格子相遇。
所以,总共有 225 - 2 = 223 种有效移动组合。
注意,有两种有效的移动组合,分别是一个车在 (1, 8) ,另一个车在 (8, 1) 。
即使棋盘状态是相同的,这两个移动组合被视为不同的,因为每个棋子移动操作是不相同的。
示例 5:

输入:pieces = ["queen","bishop"], positions = [[5,7],[3,4]]
输出:281
解释:总共有 12 * 24 = 288 种移动组合。
但是,有一些不有效的移动组合:
- 如果后停在 (6, 7) ,它会阻挡象到达 (6, 7) 或者 (7, 8) 。
- 如果后停在 (5, 6) ,它会阻挡象到达 (5, 6) ,(6, 7) 或者 (7, 8) 。
- 如果象停在 (5, 2) ,它会阻挡后到达 (5, 2) 或者 (5, 1) 。
在 288 个移动组合当中,281 个是有效的。
提示:
n == pieces.length n == positions.length1 <= n <= 4pieces 只包含字符串 "rook" ,"queen" 和 "bishop" 。- 棋盘上最多只有一个后。
1 <= ri, ci <= 8- 每一个
positions[i] 互不相同。
解法
方法一:DFS
题目最多只有 \(4\) 个棋子,每个棋子的移动方向最多有 \(8\) 种,我们可以考虑使用 DFS 搜索所有的移动组合。
我们按照顺序依次枚举每个棋子,对于每个棋子,我们可以选择不移动,或者按照规则移动,用数组 \(\textit{dist}[i]\) 记录第 \(i\) 个棋子的移动情况,其中 \(\textit{dist}[i][x][y]\) 表示第 \(i\) 个棋子经过坐标 \((x, y)\) 时的时间,用数组 \(\textit{end}[i]\) 记录第 \(i\) 个棋子的终点坐标和时间。在搜索时,我们需要分别判断当前棋子是否可以停止移动,以及当前棋子是否可以继续在当前方向移动。
我们定义方法 \(\text{checkStop}(i, x, y, t)\) 判断第 \(i\) 个棋子是否在时间 \(t\) 时停在坐标 \((x, y)\),如果对于此前的所有棋子 \(j\),都有 \(\textit{dist}[j][x][y] < t\),那么第 \(i\) 个棋子可以停止移动。
另外,我们定义方法 \(\text{checkPass}(i, x, y, t)\) 判断第 \(i\) 个棋子是否可以在时间 \(t\) 时经过坐标 \((x, y)\)。如果此前有其它棋子 \(j\) 也在时间 \(t\) 经过坐标 \((x, y)\),或者有其它棋子 \(j\) 停在 \((x, y)\),且时间不超过 \(t\),那么第 \(i\) 个棋子不能在时间 \(t\) 时经过坐标 \((x, y)\)。
时间复杂度 \(O((n \times M)^n)\),空间复杂度 \(O(n \times M)\)。其中 \(n\) 是棋子的数量,而 \(M\) 是每个棋子的移动范围。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60 | rook_dirs = [(1, 0), (-1, 0), (0, 1), (0, -1)]
bishop_dirs = [(1, 1), (1, -1), (-1, 1), (-1, -1)]
queue_dirs = rook_dirs + bishop_dirs
def get_dirs(piece: str) -> List[Tuple[int, int]]:
match piece[0]:
case "r":
return rook_dirs
case "b":
return bishop_dirs
case _:
return queue_dirs
class Solution:
def countCombinations(self, pieces: List[str], positions: List[List[int]]) -> int:
def check_stop(i: int, x: int, y: int, t: int) -> bool:
return all(dist[j][x][y] < t for j in range(i))
def check_pass(i: int, x: int, y: int, t: int) -> bool:
for j in range(i):
if dist[j][x][y] == t:
return False
if end[j][0] == x and end[j][1] == y and end[j][2] <= t:
return False
return True
def dfs(i: int) -> None:
if i >= n:
nonlocal ans
ans += 1
return
x, y = positions[i]
dist[i][:] = [[-1] * m for _ in range(m)]
dist[i][x][y] = 0
end[i] = (x, y, 0)
if check_stop(i, x, y, 0):
dfs(i + 1)
dirs = get_dirs(pieces[i])
for dx, dy in dirs:
dist[i][:] = [[-1] * m for _ in range(m)]
dist[i][x][y] = 0
nx, ny, nt = x + dx, y + dy, 1
while 1 <= nx < m and 1 <= ny < m and check_pass(i, nx, ny, nt):
dist[i][nx][ny] = nt
end[i] = (nx, ny, nt)
if check_stop(i, nx, ny, nt):
dfs(i + 1)
nx += dx
ny += dy
nt += 1
n = len(pieces)
m = 9
dist = [[[-1] * m for _ in range(m)] for _ in range(n)]
end = [(0, 0, 0) for _ in range(n)]
ans = 0
dfs(0)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98 | class Solution {
int n, m = 9, ans;
int[][][] dist;
int[][] end;
String[] pieces;
int[][] positions;
int[][] rookDirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int[][] bishopDirs = {{1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
int[][] queenDirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
public int countCombinations(String[] pieces, int[][] positions) {
n = pieces.length;
dist = new int[n][m][m];
end = new int[n][3];
ans = 0;
this.pieces = pieces;
this.positions = positions;
dfs(0);
return ans;
}
private void dfs(int i) {
if (i >= n) {
ans++;
return;
}
int x = positions[i][0], y = positions[i][1];
resetDist(i);
dist[i][x][y] = 0;
end[i] = new int[] {x, y, 0};
if (checkStop(i, x, y, 0)) {
dfs(i + 1);
}
int[][] dirs = getDirs(pieces[i]);
for (int[] dir : dirs) {
resetDist(i);
dist[i][x][y] = 0;
int nx = x + dir[0], ny = y + dir[1], nt = 1;
while (isValid(nx, ny) && checkPass(i, nx, ny, nt)) {
dist[i][nx][ny] = nt;
end[i] = new int[] {nx, ny, nt};
if (checkStop(i, nx, ny, nt)) {
dfs(i + 1);
}
nx += dir[0];
ny += dir[1];
nt++;
}
}
}
private void resetDist(int i) {
for (int j = 0; j < m; j++) {
for (int k = 0; k < m; k++) {
dist[i][j][k] = -1;
}
}
}
private boolean checkStop(int i, int x, int y, int t) {
for (int j = 0; j < i; j++) {
if (dist[j][x][y] >= t) {
return false;
}
}
return true;
}
private boolean checkPass(int i, int x, int y, int t) {
for (int j = 0; j < i; j++) {
if (dist[j][x][y] == t) {
return false;
}
if (end[j][0] == x && end[j][1] == y && end[j][2] <= t) {
return false;
}
}
return true;
}
private boolean isValid(int x, int y) {
return x >= 1 && x < m && y >= 1 && y < m;
}
private int[][] getDirs(String piece) {
char c = piece.charAt(0);
return switch (c) {
case 'r' -> rookDirs;
case 'b' -> bishopDirs;
default -> queenDirs;
};
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98 | class Solution {
public:
int countCombinations(vector<string>& pieces, vector<vector<int>>& positions) {
int n = pieces.size();
const int m = 9;
int ans = 0;
vector<vector<vector<int>>> dist(n, vector<vector<int>>(m, vector<int>(m, -1)));
vector<vector<int>> end(n, vector<int>(3));
const int rookDirs[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
const int bishopDirs[4][2] = {{1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
const int queenDirs[8][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
auto resetDist = [&](int i) {
for (int j = 0; j < m; j++) {
for (int k = 0; k < m; k++) {
dist[i][j][k] = -1;
}
}
};
auto checkStop = [&](int i, int x, int y, int t) -> bool {
for (int j = 0; j < i; j++) {
if (dist[j][x][y] >= t) {
return false;
}
}
return true;
};
auto checkPass = [&](int i, int x, int y, int t) -> bool {
for (int j = 0; j < i; j++) {
if (dist[j][x][y] == t) {
return false;
}
if (end[j][0] == x && end[j][1] == y && end[j][2] <= t) {
return false;
}
}
return true;
};
auto isValid = [&](int x, int y) -> bool {
return x >= 1 && x < m && y >= 1 && y < m;
};
auto getDirs = [&](const string& piece) -> const int(*)[2] {
char c = piece[0];
if (c == 'r') {
return rookDirs;
}
if (c == 'b') {
return bishopDirs;
}
return queenDirs;
};
auto dfs = [&](this auto&& dfs, int i) -> void {
if (i >= n) {
ans++;
return;
}
int x = positions[i][0], y = positions[i][1];
resetDist(i);
dist[i][x][y] = 0;
end[i] = {x, y, 0};
if (checkStop(i, x, y, 0)) {
dfs(i + 1);
}
const int(*dirs)[2] = getDirs(pieces[i]);
int dirsSize = (pieces[i][0] == 'q') ? 8 : 4;
for (int d = 0; d < dirsSize; d++) {
resetDist(i);
dist[i][x][y] = 0;
int nx = x + dirs[d][0], ny = y + dirs[d][1], nt = 1;
while (isValid(nx, ny) && checkPass(i, nx, ny, nt)) {
dist[i][nx][ny] = nt;
end[i] = {nx, ny, nt};
if (checkStop(i, nx, ny, nt)) {
dfs(i + 1);
}
nx += dirs[d][0];
ny += dirs[d][1];
nt++;
}
}
};
dfs(0);
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99 | func countCombinations(pieces []string, positions [][]int) (ans int) {
n := len(pieces)
m := 9
dist := make([][][]int, n)
for i := range dist {
dist[i] = make([][]int, m)
for j := range dist[i] {
dist[i][j] = make([]int, m)
}
}
end := make([][3]int, n)
rookDirs := [][2]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}}
bishopDirs := [][2]int{{1, 1}, {1, -1}, {-1, 1}, {-1, -1}}
queenDirs := [][2]int{{1, 0}, {-1, 0}, {0, 1}, {0, -1}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}}
resetDist := func(i int) {
for j := 0; j < m; j++ {
for k := 0; k < m; k++ {
dist[i][j][k] = -1
}
}
}
checkStop := func(i, x, y, t int) bool {
for j := 0; j < i; j++ {
if dist[j][x][y] >= t {
return false
}
}
return true
}
checkPass := func(i, x, y, t int) bool {
for j := 0; j < i; j++ {
if dist[j][x][y] == t {
return false
}
if end[j][0] == x && end[j][1] == y && end[j][2] <= t {
return false
}
}
return true
}
isValid := func(x, y int) bool {
return x >= 1 && x < m && y >= 1 && y < m
}
getDirs := func(piece string) [][2]int {
switch piece[0] {
case 'r':
return rookDirs
case 'b':
return bishopDirs
default:
return queenDirs
}
}
var dfs func(i int)
dfs = func(i int) {
if i >= n {
ans++
return
}
x, y := positions[i][0], positions[i][1]
resetDist(i)
dist[i][x][y] = 0
end[i] = [3]int{x, y, 0}
if checkStop(i, x, y, 0) {
dfs(i + 1)
}
dirs := getDirs(pieces[i])
for _, dir := range dirs {
resetDist(i)
dist[i][x][y] = 0
nx, ny, nt := x+dir[0], y+dir[1], 1
for isValid(nx, ny) && checkPass(i, nx, ny, nt) {
dist[i][nx][ny] = nt
end[i] = [3]int{nx, ny, nt}
if checkStop(i, nx, ny, nt) {
dfs(i + 1)
}
nx += dir[0]
ny += dir[1]
nt++
}
}
}
dfs(0)
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108 | const rookDirs: [number, number][] = [
[1, 0],
[-1, 0],
[0, 1],
[0, -1],
];
const bishopDirs: [number, number][] = [
[1, 1],
[1, -1],
[-1, 1],
[-1, -1],
];
const queenDirs = [...rookDirs, ...bishopDirs];
function countCombinations(pieces: string[], positions: number[][]): number {
const n = pieces.length;
const m = 9;
let ans = 0;
const dist = Array.from({ length: n }, () =>
Array.from({ length: m }, () => Array(m).fill(-1)),
);
const end: [number, number, number][] = Array(n).fill([0, 0, 0]);
const resetDist = (i: number) => {
for (let j = 0; j < m; j++) {
for (let k = 0; k < m; k++) {
dist[i][j][k] = -1;
}
}
};
const checkStop = (i: number, x: number, y: number, t: number): boolean => {
for (let j = 0; j < i; j++) {
if (dist[j][x][y] >= t) {
return false;
}
}
return true;
};
const checkPass = (i: number, x: number, y: number, t: number): boolean => {
for (let j = 0; j < i; j++) {
if (dist[j][x][y] === t) {
return false;
}
if (end[j][0] === x && end[j][1] === y && end[j][2] <= t) {
return false;
}
}
return true;
};
const isValid = (x: number, y: number): boolean => {
return x >= 1 && x < m && y >= 1 && y < m;
};
const getDirs = (piece: string): [number, number][] => {
switch (piece[0]) {
case 'r':
return rookDirs;
case 'b':
return bishopDirs;
default:
return queenDirs;
}
};
const dfs = (i: number) => {
if (i >= n) {
ans++;
return;
}
const [x, y] = positions[i];
resetDist(i);
dist[i][x][y] = 0;
end[i] = [x, y, 0];
if (checkStop(i, x, y, 0)) {
dfs(i + 1);
}
const dirs = getDirs(pieces[i]);
for (const [dx, dy] of dirs) {
resetDist(i);
dist[i][x][y] = 0;
let nx = x + dx,
ny = y + dy,
nt = 1;
while (isValid(nx, ny) && checkPass(i, nx, ny, nt)) {
dist[i][nx][ny] = nt;
end[i] = [nx, ny, nt];
if (checkStop(i, nx, ny, nt)) {
dfs(i + 1);
}
nx += dx;
ny += dy;
nt++;
}
}
};
dfs(0);
return ans;
}
|







