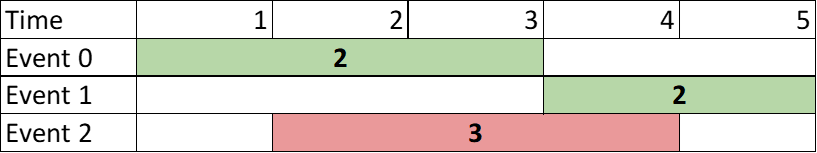题目描述
给你一个下标从 0 开始的二维整数数组 events ,其中 events[i] = [startTimei, endTimei, valuei] 。第 i 个活动开始于 startTimei ,结束于 endTimei ,如果你参加这个活动,那么你可以得到价值 valuei 。你 最多 可以参加 两个时间不重叠 活动,使得它们的价值之和 最大 。
请你返回价值之和的 最大值 。
注意,活动的开始时间和结束时间是 包括 在活动时间内的,也就是说,你不能参加两个活动且它们之一的开始时间等于另一个活动的结束时间。更具体的,如果你参加一个活动,且结束时间为 t ,那么下一个活动必须在 t + 1 或之后的时间开始。
示例 1:
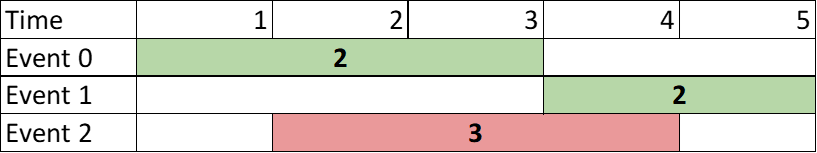
输入:events = [[1,3,2],[4,5,2],[2,4,3]]
输出:4
解释:选择绿色的活动 0 和 1 ,价值之和为 2 + 2 = 4 。
示例 2:

输入:events = [[1,3,2],[4,5,2],[1,5,5]]
输出:5
解释:选择活动 2 ,价值和为 5 。
示例 3:

输入:events = [[1,5,3],[1,5,1],[6,6,5]]
输出:8
解释:选择活动 0 和 2 ,价值之和为 3 + 5 = 8 。
提示:
2 <= events.length <= 105events[i].length == 31 <= startTimei <= endTimei <= 1091 <= valuei <= 106
解法
方法一:排序 + 二分查找
我们可以讲活动按照开始排序,然后预处理出以每个活动为作为开始的最大价值,即 \(f[i]\) 表示从第 \(i\) 个活动开始,到最后一个活动结束,选择其中一个活动的最大价值。
然后我们枚举每个活动,对于每个活动,我们使用二分查找找到第一个开始时间大于当前活动结束时间的活动,下标记为 \(\textit{idx}\),那么以当前活动为开始的最大价值就是 \(f[\textit{idx}]\),加上当前活动的价值,即为以当前活动为第一个活动,最终能获得的最大价值。求最大值即可。
时间复杂度 \(O(n \times \log n)\),空间复杂度 \(O(n)\)。其中 \(n\) 为活动的数量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | class Solution:
def maxTwoEvents(self, events: List[List[int]]) -> int:
events.sort()
n = len(events)
f = [events[-1][2]] * n
for i in range(n - 2, -1, -1):
f[i] = max(f[i + 1], events[i][2])
ans = 0
for _, e, v in events:
idx = bisect_right(events, e, key=lambda x: x[0])
if idx < n:
v += f[idx]
ans = max(ans, v)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 | class Solution {
public int maxTwoEvents(int[][] events) {
Arrays.sort(events, (a, b) -> a[0] - b[0]);
int n = events.length;
int[] f = new int[n + 1];
for (int i = n - 1; i >= 0; --i) {
f[i] = Math.max(f[i + 1], events[i][2]);
}
int ans = 0;
for (int[] e : events) {
int v = e[2];
int left = 0, right = n;
while (left < right) {
int mid = (left + right) >> 1;
if (events[mid][0] > e[1]) {
right = mid;
} else {
left = mid + 1;
}
}
if (left < n) {
v += f[left];
}
ans = Math.max(ans, v);
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | class Solution {
public:
int maxTwoEvents(vector<vector<int>>& events) {
ranges::sort(events);
int n = events.size();
vector<int> f(n + 1);
for (int i = n - 1; ~i; --i) {
f[i] = max(f[i + 1], events[i][2]);
}
int ans = 0;
for (const auto& e : events) {
int v = e[2];
int left = 0, right = n;
while (left < right) {
int mid = (left + right) >> 1;
if (events[mid][0] > e[1]) {
right = mid;
} else {
left = mid + 1;
}
}
if (left < n) {
v += f[left];
}
ans = max(ans, v);
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 | func maxTwoEvents(events [][]int) int {
sort.Slice(events, func(i, j int) bool {
return events[i][0] < events[j][0]
})
n := len(events)
f := make([]int, n+1)
for i := n - 1; i >= 0; i-- {
f[i] = max(f[i+1], events[i][2])
}
ans := 0
for _, e := range events {
v := e[2]
left, right := 0, n
for left < right {
mid := (left + right) >> 1
if events[mid][0] > e[1] {
right = mid
} else {
left = mid + 1
}
}
if left < n {
v += f[left]
}
ans = max(ans, v)
}
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | function maxTwoEvents(events: number[][]): number {
events.sort((a, b) => a[0] - b[0]);
const n = events.length;
const f: number[] = Array(n + 1).fill(0);
for (let i = n - 1; ~i; --i) {
f[i] = Math.max(f[i + 1], events[i][2]);
}
let ans = 0;
for (const [_, end, v] of events) {
let [left, right] = [0, n];
while (left < right) {
const mid = (left + right) >> 1;
if (events[mid][0] > end) {
right = mid;
} else {
left = mid + 1;
}
}
const t = left < n ? f[left] : 0;
ans = Math.max(ans, t + v);
}
return ans;
}
|