2050. 并行课程 III

题目描述

给你一个整数 n ，表示有 n 节课，课程编号从 1 到 n 。同时给你一个二维整数数组 relations ，其中 relations[j] = [prevCourse_j, nextCourse_j] ，表示课程 prevCourse_j 必须在课程 nextCourse_j 之前完成（先修课的关系）。同时给你一个下标从 0 开始的整数数组 time ，其中 time[i] 表示完成第 (i+1) 门课程需要花费的月份数。

请你根据以下规则算出完成所有课程所需要的最少月份数：

如果一门课的所有先修课都已经完成，你可以在任意时间开始这门课程。
你可以同时上 任意门课程 。

请你返回完成所有课程所需要的最少月份数。

注意：测试数据保证一定可以完成所有课程（也就是先修课的关系构成一个有向无环图）。

示例 1:

输入：n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
输出：8
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 和 2 。
课程 1 花费 3 个月，课程 2 花费 2 个月。
所以，最早开始课程 3 的时间是月份 3 ，完成所有课程所需时间为 3 + 5 = 8 个月。

示例 2：

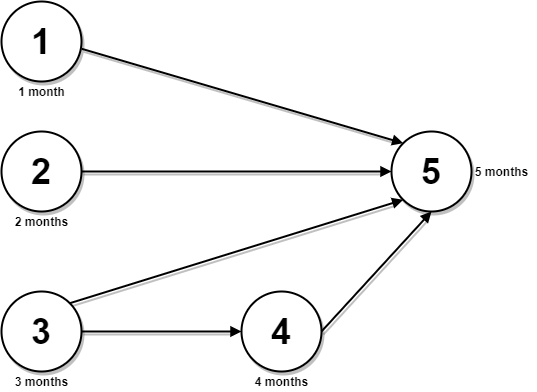
输入：n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
输出：12
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 ，2 和 3 。
在月份 1，2 和 3 分别完成这三门课程。
课程 4 需在课程 3 之后开始，也就是 3 个月后。课程 4 在 3 + 4 = 7 月完成。
课程 5 需在课程 1，2，3 和 4 之后开始，也就是在 max(1,2,3,7) = 7 月开始。
所以完成所有课程所需的最少时间为 7 + 5 = 12 个月。

提示：

1 <= n <= 5 * 10⁴
0 <= relations.length <= min(n * (n - 1) / 2, 5 * 10⁴)
relations[j].length == 2
1 <= prevCourse_j, nextCourse_j <= n
prevCourse_j != nextCourse_j
所有的先修课程对 [prevCourse_j, nextCourse_j] 都是 互不相同 的。
time.length == n
1 <= time[i] <= 10⁴
先修课程图是一个有向无环图。

解法

方法一：拓扑排序 + 动态规划

我们首先根据给定的先修课程关系，构建出一个有向无环图，对该图进行拓扑排序，然后根据拓扑排序的结果，使用动态规划求出完成所有课程所需要的最少时间。

我们定义以下几个数据结构或变量：

邻接表 $g$ 存储有向无环图，同时使用一个数组 $indeg$ 存储每个节点的入度；
队列 $q$ 存储所有入度为 $0$ 的节点；
数组 $f$ 存储每个节点的最早完成时间，初始时 $f[i] = 0$；
变量 $ans$ 记录最终的答案，初始时 $ans = 0$；

当 $q$ 非空时，依次取出队首节点 $i$，遍历 $g[i]$ 中的每个节点 $j$，更新 $f[j] = \max(f[j], f[i] + time[j])$，同时更新 $ans = \max(ans, f[j])$，并将 $j$ 的入度减 $1$，如果此时 $j$ 的入度为 $0$，则将 $j$ 加入队列 $q$ 中；

最终返回 $ans$。

时间复杂度 $O(m + n)$，空间复杂度 $O(m + n)$。其中 $m$ 是数组 $relations$ 的长度。

Python3JavaC++GoTypeScript

class Solution:
    def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int:
        g = defaultdict(list)
        indeg = [0] * n
        for a, b in relations:
            g[a - 1].append(b - 1)
            indeg[b - 1] += 1
        q = deque()
        f = [0] * n
        ans = 0
        for i, (v, t) in enumerate(zip(indeg, time)):
            if v == 0:
                q.append(i)
                f[i] = t
                ans = max(ans, t)
        while q:
            i = q.popleft()
            for j in g[i]:
                f[j] = max(f[j], f[i] + time[j])
                ans = max(ans, f[j])
                indeg[j] -= 1
                if indeg[j] == 0:
                    q.append(j)
        return ans

class Solution {
    public int minimumTime(int n, int[][] relations, int[] time) {
        List<Integer>[] g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        int[] indeg = new int[n];
        for (int[] e : relations) {
            int a = e[0] - 1, b = e[1] - 1;
            g[a].add(b);
            ++indeg[b];
        }
        Deque<Integer> q = new ArrayDeque<>();
        int[] f = new int[n];
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            int v = indeg[i], t = time[i];
            if (v == 0) {
                q.offer(i);
                f[i] = t;
                ans = Math.max(ans, t);
            }
        }
        while (!q.isEmpty()) {
            int i = q.pollFirst();
            for (int j : g[i]) {
                f[j] = Math.max(f[j], f[i] + time[j]);
                ans = Math.max(ans, f[j]);
                if (--indeg[j] == 0) {
                    q.offer(j);
                }
            }
        }
        return ans;
    }
}

class Solution {
public:
    int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {
        vector<vector<int>> g(n);
        vector<int> indeg(n);
        for (auto& e : relations) {
            int a = e[0] - 1, b = e[1] - 1;
            g[a].push_back(b);
            ++indeg[b];
        }
        queue<int> q;
        vector<int> f(n);
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            int v = indeg[i], t = time[i];
            if (v == 0) {
                q.push(i);
                f[i] = t;
                ans = max(ans, t);
            }
        }
        while (!q.empty()) {
            int i = q.front();
            q.pop();
            for (int j : g[i]) {
                if (--indeg[j] == 0) {
                    q.push(j);
                }
                f[j] = max(f[j], f[i] + time[j]);
                ans = max(ans, f[j]);
            }
        }
        return ans;
    }
};

func minimumTime(n int, relations [][]int, time []int) int {
    g := make([][]int, n)
    indeg := make([]int, n)
    for _, e := range relations {
        a, b := e[0]-1, e[1]-1
        g[a] = append(g[a], b)
        indeg[b]++
    }
    f := make([]int, n)
    q := []int{}
    ans := 0
    for i, v := range indeg {
        if v == 0 {
            q = append(q, i)
            f[i] = time[i]
            ans = max(ans, time[i])
        }
    }
    for len(q) > 0 {
        i := q[0]
        q = q[1:]
        for _, j := range g[i] {
            indeg[j]--
            if indeg[j] == 0 {
                q = append(q, j)
            }
            f[j] = max(f[j], f[i]+time[j])
            ans = max(ans, f[j])
        }
    }
    return ans
}

function minimumTime(n: number, relations: number[][], time: number[]): number {
    const g: number[][] = Array(n)
        .fill(0)
        .map(() => []);
    const indeg: number[] = Array(n).fill(0);
    for (const [a, b] of relations) {
        g[a - 1].push(b - 1);
        ++indeg[b - 1];
    }
    const q: number[] = [];
    const f: number[] = Array(n).fill(0);
    let ans: number = 0;
    for (let i = 0; i < n; ++i) {
        if (indeg[i] === 0) {
            q.push(i);
            f[i] = time[i];
            ans = Math.max(ans, f[i]);
        }
    }
    while (q.length > 0) {
        const i = q.shift()!;
        for (const j of g[i]) {
            f[j] = Math.max(f[j], f[i] + time[j]);
            ans = Math.max(ans, f[j]);
            if (--indeg[j] === 0) {
                q.push(j);
            }
        }
    }
    return ans;
}

2050. 并行课程 III

题目描述

解法

方法一：拓扑排序 + 动态规划

评论