跳转至

2022. 将一维数组转变成二维数组

题目描述

给你一个下标从 0 开始的一维整数数组 original 和两个整数 m 和  n 。你需要使用 original 中 所有 元素创建一个 m 行 n 列的二维数组。

original 中下标从 0 到 n - 1 （都 包含 ）的元素构成二维数组的第一行，下标从 n 到 2 * n - 1 （都 包含 ）的元素构成二维数组的第二行，依此类推。

请你根据上述过程返回一个 m x n 的二维数组。如果无法构成这样的二维数组，请你返回一个空的二维数组。

 

示例 1：

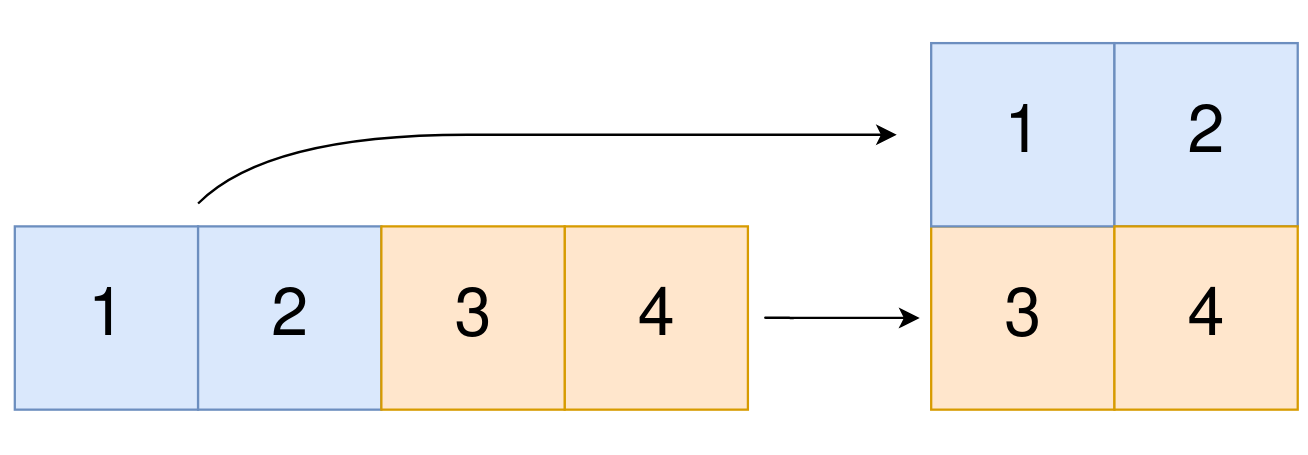
输入：original = [1,2,3,4], m = 2, n = 2
输出：[[1,2],[3,4]]
解释：
构造出的二维数组应该包含 2 行 2 列。
original 中第一个 n=2 的部分为 [1,2] ，构成二维数组的第一行。
original 中第二个 n=2 的部分为 [3,4] ，构成二维数组的第二行。

示例 2：

输入：original = [1,2,3], m = 1, n = 3
输出：[[1,2,3]]
解释：
构造出的二维数组应该包含 1 行 3 列。
将 original 中所有三个元素放入第一行中，构成要求的二维数组。

示例 3：

输入：original = [1,2], m = 1, n = 1
输出：[]
解释：
original 中有 2 个元素。
无法将 2 个元素放入到一个 1x1 的二维数组中，所以返回一个空的二维数组。

示例 4：

输入：original = [3], m = 1, n = 2
输出：[]
解释：
original 中只有 1 个元素。
无法将 1 个元素放满一个 1x2 的二维数组，所以返回一个空的二维数组。

 

提示：

  • 1 <= original.length <= 5 * 104
  • 1 <= original[i] <= 105
  • 1 <= m, n <= 4 * 104

解法

方法一：模拟

根据题目描述，我们知道，要想构造出一个 $m$ 行 $n$ 列的二维数组，需要满足 $m \times n$ 等于原数组的长度。如果不满足，直接返回空数组即可。

如果满足，我们可以按照题目描述的过程，将原数组中的元素依次放入二维数组中即可。

时间复杂度 $O(m \times n)$，其中 $m$ 和 $n$ 分别为二维数组的行数和列数。忽略答案的空间消耗，空间复杂度 $O(1)$。

1
2
3
4
5
class Solution:
    def construct2DArray(self, original: List[int], m: int, n: int) -> List[List[int]]:
        if m * n != len(original):
            return []
        return [original[i : i + n] for i in range(0, m * n, n)]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
class Solution {
    public int[][] construct2DArray(int[] original, int m, int n) {
        if (m * n != original.length) {
            return new int[0][0];
        }
        int[][] ans = new int[m][n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                ans[i][j] = original[i * n + j];
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution {
public:
    vector<vector<int>> construct2DArray(vector<int>& original, int m, int n) {
        if (m * n != original.size()) {
            return {};
        }
        vector<vector<int>> ans(m, vector<int>(n));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                ans[i][j] = original[i * n + j];
            }
        }
        return ans;
    }
};

1
2
3
4
5
6
7
8
9
func construct2DArray(original []int, m int, n int) (ans [][]int) {
    if m*n != len(original) {
        return [][]int{}
    }
    for i := 0; i < m*n; i += n {
        ans = append(ans, original[i:i+n])
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
function construct2DArray(original: number[], m: number, n: number): number[][] {
    if (m * n != original.length) {
        return [];
    }
    const ans: number[][] = [];
    for (let i = 0; i < m * n; i += n) {
        ans.push(original.slice(i, i + n));
    }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
/**
 * @param {number[]} original
 * @param {number} m
 * @param {number} n
 * @return {number[][]}
 */
var construct2DArray = function (original, m, n) {
    if (m * n != original.length) {
        return [];
    }
    const ans = [];
    for (let i = 0; i < m * n; i += n) {
        ans.push(original.slice(i, i + n));
    }
    return ans;
};

评论