
题目描述
一条街上有很多的路灯,路灯的坐标由数组 lights 的形式给出。 每个 lights[i] = [positioni, rangei] 代表坐标为 positioni 的路灯照亮的范围为 [positioni - rangei, positioni + rangei] (包括顶点)。
位置 p 的亮度由能够照到 p的路灯的数量来决定的。
给出 lights, 返回最亮的位置 。如果有很多,返回坐标最小的。
示例 1:
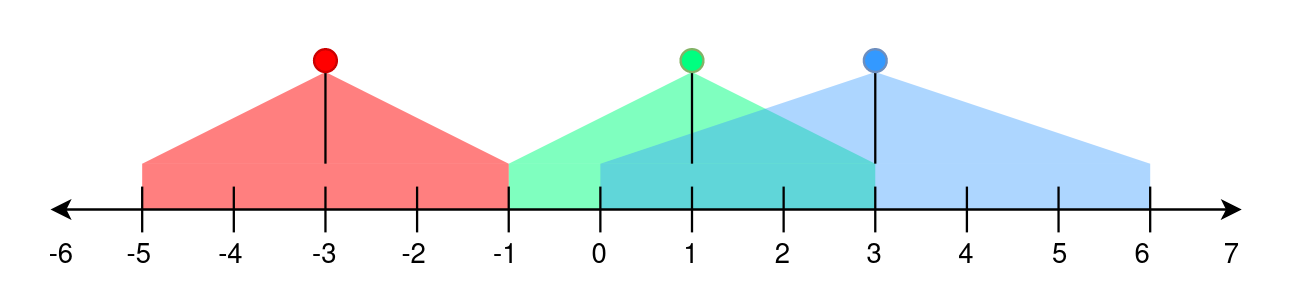
输入: lights = [[-3,2],[1,2],[3,3]]
输出: -1
解释:
第一个路灯照亮的范围是[(-3) - 2, (-3) + 2] = [-5, -1].
第二个路灯照亮的范围是 [1 - 2, 1 + 2] = [-1, 3].
第三个路灯照亮的范围是 [3 - 3, 3 + 3] = [0, 6].
坐标-1被第一个和第二个路灯照亮,亮度为2
坐标0,1,2都被第二个和第三个路灯照亮,亮度为2.
对于以上坐标,-1最小,所以返回-1
示例 2:
输入: lights = [[1,0],[0,1]]
输出: 1
示例 3:
输入: lights = [[1,2]]
输出: -1
提示:
1 <= lights.length <= 105lights[i].length == 2-108 <= positioni <= 1080 <= rangei <= 108
解法
方法一:差分数组 + 哈希表 + 排序
我们可以将每个路灯照亮的范围看作是一个区间,区间左端点 \(l = position_i - range_i\),区间右端点 \(r = position_i + range_i\)。我们可以利用差分数组的思想,对于每个区间 \([l, r]\),将位置 \(l\) 的值加 \(1\),将位置 \(r + 1\) 的值减 \(1\),用哈希表维护每个位置的变化值。
然后从小到大遍历每个位置,计算当前位置的亮度 \(s\),如果此前的最大亮度 \(mx \lt s\),则更新最大亮度 \(mx = s\),并记录当前位置 \(ans = i\)。
最后返回 \(ans\) 即可。
时间复杂度 \(O(n \times \log n)\),空间复杂度 \(O(n)\)。其中 \(n\) 为 \(lights\) 的长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | class Solution:
def brightestPosition(self, lights: List[List[int]]) -> int:
d = defaultdict(int)
for i, j in lights:
l, r = i - j, i + j
d[l] += 1
d[r + 1] -= 1
ans = s = mx = 0
for k in sorted(d):
s += d[k]
if mx < s:
mx = s
ans = k
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | class Solution {
public int brightestPosition(int[][] lights) {
TreeMap<Integer, Integer> d = new TreeMap<>();
for (var x : lights) {
int l = x[0] - x[1], r = x[0] + x[1];
d.merge(l, 1, Integer::sum);
d.merge(r + 1, -1, Integer::sum);
}
int ans = 0, s = 0, mx = 0;
for (var x : d.entrySet()) {
int v = x.getValue();
s += v;
if (mx < s) {
mx = s;
ans = x.getKey();
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | class Solution {
public:
int brightestPosition(vector<vector<int>>& lights) {
map<int, int> d;
for (auto& x : lights) {
int l = x[0] - x[1], r = x[0] + x[1];
++d[l];
--d[r + 1];
}
int ans = 0, s = 0, mx = 0;
for (auto& [i, v] : d) {
s += v;
if (mx < s) {
mx = s;
ans = i;
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | func brightestPosition(lights [][]int) (ans int) {
d := map[int]int{}
for _, x := range lights {
l, r := x[0]-x[1], x[0]+x[1]
d[l]++
d[r+1]--
}
keys := make([]int, 0, len(d))
for i := range d {
keys = append(keys, i)
}
sort.Ints(keys)
mx, s := 0, 0
for _, i := range keys {
s += d[i]
if mx < s {
mx = s
ans = i
}
}
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | /**
* @param {number[][]} lights
* @return {number}
*/
var brightestPosition = function (lights) {
const d = new Map();
for (const [i, j] of lights) {
const l = i - j;
const r = i + j;
d.set(l, (d.get(l) ?? 0) + 1);
d.set(r + 1, (d.get(r + 1) ?? 0) - 1);
}
const keys = [];
for (const k of d.keys()) {
keys.push(k);
}
keys.sort((a, b) => a - b);
let ans = 0;
let s = 0;
let mx = 0;
for (const i of keys) {
s += d.get(i);
if (mx < s) {
mx = s;
ans = i;
}
}
return ans;
};
|

