跳转至

1981. 最小化目标值与所选元素的差

题目描述

给你一个大小为 m x n 的整数矩阵 mat 和一个整数 target 。

从矩阵的 每一行 中选择一个整数，你的目标是 最小化 所有选中元素之 和 与目标值 target 的 绝对差 。

返回 最小的绝对差 。

a 和 b 两数字的 绝对差 是 a - b 的绝对值。

 

示例 1：

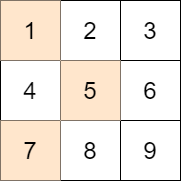
输入：mat = [[1,2,3],[4,5,6],[7,8,9]], target = 13
输出：0
解释：一种可能的最优选择方案是：
- 第一行选出 1
- 第二行选出 5
- 第三行选出 7
所选元素的和是 13 ，等于目标值，所以绝对差是 0 。

示例 2：

输入：mat = [[1],[2],[3]], target = 100
输出：94
解释：唯一一种选择方案是：
- 第一行选出 1
- 第二行选出 2
- 第三行选出 3
所选元素的和是 6 ，绝对差是 94 。

示例 3：

输入：mat = [[1,2,9,8,7]], target = 6
输出：1
解释：最优的选择方案是选出第一行的 7 。
绝对差是 1 。

 

提示：

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 70
  • 1 <= mat[i][j] <= 70
  • 1 <= target <= 800

解法

方法一：动态规划（分组背包）

设 $f[i][j]$ 表示前 $i$ 行是否能选出元素和为 $j$，则有状态转移方程：

$$ f[i][j] = \begin{cases} 1 & \textit{如果存在 } x \in row[i] \textit{ 使得 } f[i - 1][j - x] = 1 \ 0 & \textit{否则} \end{cases} $$

其中 $row[i]$ 表示第 $i$ 行的元素集合。

由于 $f[i][j]$ 只与 $f[i - 1][j]$ 有关，因此我们可以使用滚动数组优化空间复杂度。

最后，遍历 $f$ 数组，找出最小的绝对差即可。

时间复杂度 $O(m^2 \times n \times C)$，空间复杂度 $O(m \times C)$。其中 $m$ 和 $n$ 分别为矩阵的行数和列数；而 $C$ 为矩阵元素的最大值。

1
2
3
4
5
6
class Solution:
    def minimizeTheDifference(self, mat: List[List[int]], target: int) -> int:
        f = {0}
        for row in mat:
            f = set(a + b for a in f for b in row)
        return min(abs(v - target) for v in f)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int minimizeTheDifference(int[][] mat, int target) {
        boolean[] f = {true};
        for (var row : mat) {
            int mx = 0;
            for (int x : row) {
                mx = Math.max(mx, x);
            }
            boolean[] g = new boolean[f.length + mx];
            for (int x : row) {
                for (int j = x; j < f.length + x; ++j) {
                    g[j] |= f[j - x];
                }
            }
            f = g;
        }
        int ans = 1 << 30;
        for (int j = 0; j < f.length; ++j) {
            if (f[j]) {
                ans = Math.min(ans, Math.abs(j - target));
            }
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int minimizeTheDifference(int[][] mat, int target) {
        Set<Integer> f = new HashSet<>();
        f.add(0);
        for (var row : mat) {
            Set<Integer> g = new HashSet<>();
            for (int a : f) {
                for (int b : row) {
                    g.add(a + b);
                }
            }
            f = g;
        }
        int ans = 1 << 30;
        for (int v : f) {
            ans = Math.min(ans, Math.abs(v - target));
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int minimizeTheDifference(vector<vector<int>>& mat, int target) {
        vector<int> f = {1};
        for (auto& row : mat) {
            int mx = *max_element(row.begin(), row.end());
            vector<int> g(f.size() + mx);
            for (int x : row) {
                for (int j = x; j < f.size() + x; ++j) {
                    g[j] |= f[j - x];
                }
            }
            f = move(g);
        }
        int ans = 1 << 30;
        for (int j = 0; j < f.size(); ++j) {
            if (f[j]) {
                ans = min(ans, abs(j - target));
            }
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func minimizeTheDifference(mat [][]int, target int) int {
    f := []int{1}
    for _, row := range mat {
        mx := slices.Max(row)
        g := make([]int, len(f)+mx)
        for _, x := range row {
            for j := x; j < len(f)+x; j++ {
                g[j] |= f[j-x]
            }
        }
        f = g
    }
    ans := 1 << 30
    for j, v := range f {
        if v == 1 {
            ans = min(ans, abs(j-target))
        }
    }
    return ans
}

func abs(x int) int {
    if x < 0 {
        return -x
    }
    return x
}

评论