1975. 最大方阵和

题目描述

给你一个 n x n 的整数方阵 matrix 。你可以执行以下操作 任意次 ：

选择 matrix 中相邻两个元素，并将它们都乘以 -1 。

如果两个元素有 公共边 ，那么它们就是相邻的。

你的目的是 最大化 方阵元素的和。请你在执行以上操作之后，返回方阵的最大和。

示例 1：

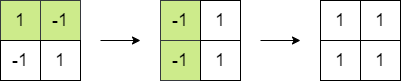
输入：matrix = [[1,-1],[-1,1]]
输出：4
解释：我们可以执行以下操作使和等于 4 ：
- 将第一行的 2 个元素乘以 -1 。
- 将第一列的 2 个元素乘以 -1 。

示例 2：

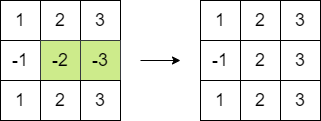
输入：matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]
输出：16
解释：我们可以执行以下操作使和等于 16 ：
- 将第二行的最后 2 个元素乘以 -1 。

提示：

n == matrix.length == matrix[i].length
2 <= n <= 250
-10⁵ <= matrix[i][j] <= 10⁵

解法

方法一：贪心

如果矩阵中存在零，或者矩阵中负数的个数为偶数，那么最大和就是矩阵中所有元素的绝对值之和。

否则，说明矩阵中有奇数个负数，最终一定会剩下一个负数，我们选择绝对值最小的数，将其变为负数，这样可以使得最终的和最大。

时间复杂度 \(O(m \times n)\)，其中 \(m\) 和 \(n\) 分别是矩阵的行数和列数。空间复杂度 \(O(1)\)。

Python3JavaC++GoTypeScriptRustJavaScript

class Solution:
    def maxMatrixSum(self, matrix: List[List[int]]) -> int:
        mi = inf
        s = cnt = 0
        for row in matrix:
            for x in row:
                cnt += x < 0
                y = abs(x)
                mi = min(mi, y)
                s += y
        return s if cnt % 2 == 0 else s - mi * 2

class Solution {
    public long maxMatrixSum(int[][] matrix) {
        long s = 0;
        int mi = 1 << 30, cnt = 0;
        for (var row : matrix) {
            for (int x : row) {
                cnt += x < 0 ? 1 : 0;
                int y = Math.abs(x);
                mi = Math.min(mi, y);
                s += y;
            }
        }
        return cnt % 2 == 0 ? s : s - mi * 2;
    }
}

class Solution {
public:
    long long maxMatrixSum(vector<vector<int>>& matrix) {
        long long s = 0;
        int mi = 1 << 30, cnt = 0;
        for (const auto& row : matrix) {
            for (int x : row) {
                cnt += x < 0 ? 1 : 0;
                int y = abs(x);
                mi = min(mi, y);
                s += y;
            }
        }
        return cnt % 2 == 0 ? s : s - mi * 2;
    }
};

func maxMatrixSum(matrix [][]int) int64 {
    var s int64
    mi, cnt := 1<<30, 0
    for _, row := range matrix {
        for _, x := range row {
            if x < 0 {
                cnt++
                x = -x
            }
            mi = min(mi, x)
            s += int64(x)
        }
    }
    if cnt%2 == 0 {
        return s
    }
    return s - int64(mi*2)
}

function maxMatrixSum(matrix: number[][]): number {
    let [s, cnt, mi] = [0, 0, Infinity];
    for (const row of matrix) {
        for (const x of row) {
            if (x < 0) {
                ++cnt;
            }
            const y = Math.abs(x);
            s += y;
            mi = Math.min(mi, y);
        }
    }
    return cnt % 2 === 0 ? s : s - 2 * mi;
}

impl Solution {
    pub fn max_matrix_sum(matrix: Vec<Vec<i32>>) -> i64 {
        let mut s = 0;
        let mut mi = i32::MAX;
        let mut cnt = 0;
        for row in matrix {
            for &x in row.iter() {
                cnt += if x < 0 { 1 } else { 0 };
                let y = x.abs();
                mi = mi.min(y);
                s += y as i64;
            }
        }
        if cnt % 2 == 0 {
            s
        } else {
            s - (mi as i64 * 2)
        }
    }
}

/**
 * @param {number[][]} matrix
 * @return {number}
 */
var maxMatrixSum = function (matrix) {
    let [s, cnt, mi] = [0, 0, Infinity];
    for (const row of matrix) {
        for (const x of row) {
            if (x < 0) {
                ++cnt;
            }
            const y = Math.abs(x);
            s += y;
            mi = Math.min(mi, y);
        }
    }
    return cnt % 2 === 0 ? s : s - 2 * mi;
};

1975. 最大方阵和

题目描述

解法

方法一：贪心

评论