


题目描述
给你一个下标从 1 开始的二进制矩阵,其中 0 表示陆地,1 表示水域。同时给你 row 和 col 分别表示矩阵中行和列的数目。
一开始在第 0 天,整个 矩阵都是 陆地 。但每一天都会有一块新陆地被 水 淹没变成水域。给你一个下标从 1 开始的二维数组 cells ,其中 cells[i] = [ri, ci] 表示在第 i 天,第 ri 行 ci 列(下标都是从 1 开始)的陆地会变成 水域 (也就是 0 变成 1 )。
你想知道从矩阵最 上面 一行走到最 下面 一行,且只经过陆地格子的 最后一天 是哪一天。你可以从最上面一行的 任意 格子出发,到达最下面一行的 任意 格子。你只能沿着 四个 基本方向移动(也就是上下左右)。
请返回只经过陆地格子能从最 上面 一行走到最 下面 一行的 最后一天 。
示例 1:
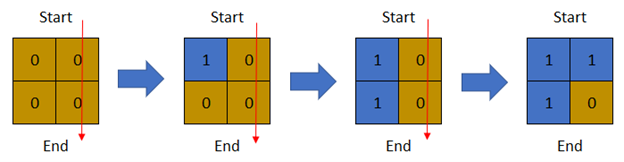
输入:row = 2, col = 2, cells = [[1,1],[2,1],[1,2],[2,2]]
输出:2
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 2 天。
示例 2:
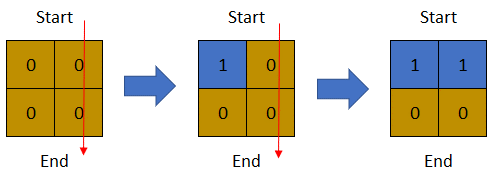
输入:row = 2, col = 2, cells = [[1,1],[1,2],[2,1],[2,2]]
输出:1
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 1 天。
示例 3:
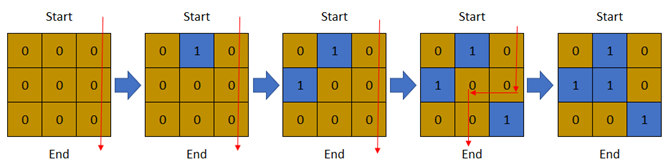
输入:row = 3, col = 3, cells = [[1,2],[2,1],[3,3],[2,2],[1,1],[1,3],[2,3],[3,2],[3,1]]
输出:3
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 3 天。
提示:
2 <= row, col <= 2 * 1044 <= row * col <= 2 * 104cells.length == row * col1 <= ri <= row1 <= ci <= colcells 中的所有格子坐标都是 唯一 的。
解法
方法一:二分查找 + BFS
我们注意到,如果我们能在第 \(k\) 天从最上面一行走到最下面一行,那么对于任意 \(0 \lt k' \lt k\),我们也能在第 \(k'\) 天从最上面一行走到最下面一行。这存在着单调性,因此,我们可以使用二分查找,找到最大的 \(k\),使得我们能在第 \(k\) 天从最上面一行走到最下面一行。
我们定义二分查找的左边界 \(l = 1\),右边界 \(r = |cells|\),其中 \(|cells|\) 表示数组 \(cells\) 的长度。然后,我们二分枚举 \(k\),对于每一个 \(k\),我们取 \(\textit{cells}\) 的前 \(k\) 个元素,将这些元素对应的格子变成水域,然后使用广度优先搜索,从最上面一行开始,尝试走到最下面一行。如果我们能走到最下面一行,那么说明我们可以在第 \(k\) 天从最上面一行走到最下面一行,我们就将左边界 \(l\) 更新为 \(k\),否则,我们将右边界 \(r\) 更新为 \(k - 1\)。
时间复杂度 \(O(m \times n \times \log (m \times n))\),空间复杂度 \(O(m \times n)\)。其中 \(m\) 和 \(n\) 分别表示矩阵的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution:
def latestDayToCross(self, row: int, col: int, cells: List[List[int]]) -> int:
def check(k: int) -> bool:
g = [[0] * col for _ in range(row)]
for i, j in cells[:k]:
g[i - 1][j - 1] = 1
q = [(0, j) for j in range(col) if g[0][j] == 0]
for x, y in q:
if x == row - 1:
return True
for a, b in pairwise(dirs):
nx, ny = x + a, y + b
if 0 <= nx < row and 0 <= ny < col and g[nx][ny] == 0:
q.append((nx, ny))
g[nx][ny] = 1
return False
n = row * col
l, r = 1, n
dirs = (-1, 0, 1, 0, -1)
while l < r:
mid = (l + r + 1) >> 1
if check(mid):
l = mid
else:
r = mid - 1
return l
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51 | class Solution {
private int[][] cells;
private int m;
private int n;
public int latestDayToCross(int row, int col, int[][] cells) {
int l = 1, r = cells.length;
this.cells = cells;
this.m = row;
this.n = col;
while (l < r) {
int mid = (l + r + 1) >> 1;
if (check(mid)) {
l = mid;
} else {
r = mid - 1;
}
}
return l;
}
private boolean check(int k) {
int[][] g = new int[m][n];
for (int i = 0; i < k; i++) {
g[cells[i][0] - 1][cells[i][1] - 1] = 1;
}
final int[] dirs = {-1, 0, 1, 0, -1};
Deque<int[]> q = new ArrayDeque<>();
for (int j = 0; j < n; j++) {
if (g[0][j] == 0) {
q.offer(new int[] {0, j});
g[0][j] = 1;
}
}
while (!q.isEmpty()) {
int[] p = q.poll();
int x = p[0], y = p[1];
if (x == m - 1) {
return true;
}
for (int i = 0; i < 4; i++) {
int nx = x + dirs[i], ny = y + dirs[i + 1];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && g[nx][ny] == 0) {
q.offer(new int[] {nx, ny});
g[nx][ny] = 1;
}
}
}
return false;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46 | class Solution {
public:
int latestDayToCross(int row, int col, vector<vector<int>>& cells) {
int l = 1, r = cells.size();
int g[row][col];
int dirs[5] = {0, 1, 0, -1, 0};
auto check = [&](int k) -> bool {
memset(g, 0, sizeof(g));
for (int i = 0; i < k; ++i) {
g[cells[i][0] - 1][cells[i][1] - 1] = 1;
}
queue<pair<int, int>> q;
for (int j = 0; j < col; ++j) {
if (g[0][j] == 0) {
q.emplace(0, j);
g[0][j] = 1;
}
}
while (!q.empty()) {
auto [x, y] = q.front();
q.pop();
if (x == row - 1) {
return true;
}
for (int i = 0; i < 4; ++i) {
int nx = x + dirs[i];
int ny = y + dirs[i + 1];
if (nx >= 0 && nx < row && ny >= 0 && ny < col && g[nx][ny] == 0) {
q.emplace(nx, ny);
g[nx][ny] = 1;
}
}
}
return false;
};
while (l < r) {
int mid = (l + r + 1) >> 1;
if (check(mid)) {
l = mid;
} else {
r = mid - 1;
}
}
return l;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44 | func latestDayToCross(row int, col int, cells [][]int) int {
l, r := 1, len(cells)
dirs := [5]int{-1, 0, 1, 0, -1}
check := func(k int) bool {
g := make([][]int, row)
for i := range g {
g[i] = make([]int, col)
}
for i := 0; i < k; i++ {
g[cells[i][0]-1][cells[i][1]-1] = 1
}
q := [][2]int{}
for j := 0; j < col; j++ {
if g[0][j] == 0 {
g[0][j] = 1
q = append(q, [2]int{0, j})
}
}
for len(q) > 0 {
x, y := q[0][0], q[0][1]
q = q[1:]
if x == row-1 {
return true
}
for i := 0; i < 4; i++ {
nx, ny := x+dirs[i], y+dirs[i+1]
if nx >= 0 && nx < row && ny >= 0 && ny < col && g[nx][ny] == 0 {
g[nx][ny] = 1
q = append(q, [2]int{nx, ny})
}
}
}
return false
}
for l < r {
mid := (l + r + 1) >> 1
if check(mid) {
l = mid
} else {
r = mid - 1
}
}
return l
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 | function latestDayToCross(row: number, col: number, cells: number[][]): number {
let [l, r] = [1, cells.length];
const check = (k: number): boolean => {
const g: number[][] = Array.from({ length: row }, () => Array(col).fill(0));
for (let i = 0; i < k; ++i) {
const [x, y] = cells[i];
g[x - 1][y - 1] = 1;
}
const q: number[][] = [];
for (let j = 0; j < col; ++j) {
if (g[0][j] === 0) {
q.push([0, j]);
g[0][j] = 1;
}
}
const dirs: number[] = [-1, 0, 1, 0, -1];
for (const [x, y] of q) {
if (x === row - 1) {
return true;
}
for (let i = 0; i < 4; ++i) {
const nx = x + dirs[i];
const ny = y + dirs[i + 1];
if (nx >= 0 && nx < row && ny >= 0 && ny < col && g[nx][ny] === 0) {
q.push([nx, ny]);
g[nx][ny] = 1;
}
}
}
return false;
};
while (l < r) {
const mid = (l + r + 1) >> 1;
if (check(mid)) {
l = mid;
} else {
r = mid - 1;
}
}
return l;
}
|
方法二:并查集
我们可以先将所有的陆地格子初始化为 \(1\),然后倒序遍历数组 \(\textit{cells}\),将每个格子对应的陆地格子变成 \(0\),并将其与上下左右的陆地格子合并。我们还需要维护两个虚拟节点 \(s\) 和 \(t\),分别表示最上面一行和最下面一行的虚拟节点。如果 \(s\) 和 \(t\) 在并查集中连通,那么说明我们可以在第 \(i\) 天从最上面一行走到最下面一行。
时间复杂度 \(O(m \times n \times \alpha(m \times n))\),空间复杂度 \(O(m \times n)\)。其中 \(m\) 和 \(n\) 分别表示矩阵的行数和列数,而 \(\alpha\) 表示 Ackermann 函数的反函数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 | class UnionFind:
def __init__(self, n):
self.p = list(range(n))
self.size = [1] * n
def find(self, x):
if self.p[x] != x:
self.p[x] = self.find(self.p[x])
return self.p[x]
def union(self, a, b):
pa, pb = self.find(a), self.find(b)
if pa == pb:
return False
if self.size[pa] > self.size[pb]:
self.p[pb] = pa
self.size[pa] += self.size[pb]
else:
self.p[pa] = pb
self.size[pb] += self.size[pa]
return True
class Solution:
def latestDayToCross(self, row: int, col: int, cells: List[List[int]]) -> int:
mn = len(cells)
uf = UnionFind(mn + 2)
s, t = mn, mn + 1
dirs = (-1, 0, 1, 0, -1)
g = [[1] * col for _ in range(row)]
for i in range(mn - 1, -1, -1):
x, y = cells[i][0] - 1, cells[i][1] - 1
g[x][y] = 0
for a, b in pairwise(dirs):
nx, ny = x + a, y + b
if 0 <= nx < row and 0 <= ny < col and g[nx][ny] == 0:
uf.union(x * col + y, nx * col + ny)
if x == 0:
uf.union(y, s)
if x == row - 1:
uf.union(x * col + y, t)
if uf.find(s) == uf.find(t):
return i
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67 | class UnionFind {
private final int[] p;
private final int[] size;
public UnionFind(int n) {
p = new int[n];
size = new int[n];
for (int i = 0; i < n; ++i) {
p[i] = i;
size[i] = 1;
}
}
public int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
public boolean union(int a, int b) {
int pa = find(a), pb = find(b);
if (pa == pb) {
return false;
}
if (size[pa] > size[pb]) {
p[pb] = pa;
size[pa] += size[pb];
} else {
p[pa] = pb;
size[pb] += size[pa];
}
return true;
}
}
class Solution {
public int latestDayToCross(int row, int col, int[][] cells) {
int mn = cells.length;
UnionFind uf = new UnionFind(mn + 2);
int s = mn, t = mn + 1;
int[][] g = new int[row][col];
for (var e : g) {
Arrays.fill(e, 1);
}
final int[] dirs = {-1, 0, 1, 0, -1};
for (int i = mn - 1;; --i) {
int x = cells[i][0] - 1, y = cells[i][1] - 1;
g[x][y] = 0;
for (int j = 0; j < 4; ++j) {
int nx = x + dirs[j], ny = y + dirs[j + 1];
if (nx >= 0 && nx < row && ny >= 0 && ny < col && g[nx][ny] == 0) {
uf.union(x * col + y, nx * col + ny);
}
}
if (x == 0) {
uf.union(s, x * col + y);
}
if (x == row - 1) {
uf.union(t, x * col + y);
}
if (uf.find(s) == uf.find(t)) {
return i;
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63 | class UnionFind {
public:
UnionFind(int n) {
p = vector<int>(n);
size = vector<int>(n, 1);
iota(p.begin(), p.end(), 0);
}
bool unite(int a, int b) {
int pa = find(a), pb = find(b);
if (pa == pb) {
return false;
}
if (size[pa] > size[pb]) {
p[pb] = pa;
size[pa] += size[pb];
} else {
p[pa] = pb;
size[pb] += size[pa];
}
return true;
}
int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
private:
vector<int> p, size;
};
class Solution {
public:
int latestDayToCross(int row, int col, vector<vector<int>>& cells) {
int mn = cells.size();
UnionFind uf(mn + 2);
int s = mn, t = mn + 1;
vector<vector<int>> g(row, vector<int>(col, 1));
const int dirs[5] = {0, 1, 0, -1, 0};
for (int i = mn - 1;; --i) {
int x = cells[i][0] - 1, y = cells[i][1] - 1;
g[x][y] = 0;
for (int j = 0; j < 4; ++j) {
int nx = x + dirs[j], ny = y + dirs[j + 1];
if (nx >= 0 && nx < row && ny >= 0 && ny < col && g[nx][ny] == 0) {
uf.unite(x * col + y, nx * col + ny);
}
}
if (x == 0) {
uf.unite(s, x * col + y);
}
if (x == row - 1) {
uf.unite(t, x * col + y);
}
if (uf.find(s) == uf.find(t)) {
return i;
}
}
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68 | type unionFind struct {
p, size []int
}
func newUnionFind(n int) *unionFind {
p := make([]int, n)
size := make([]int, n)
for i := range p {
p[i] = i
size[i] = 1
}
return &unionFind{p, size}
}
func (uf *unionFind) find(x int) int {
if uf.p[x] != x {
uf.p[x] = uf.find(uf.p[x])
}
return uf.p[x]
}
func (uf *unionFind) union(a, b int) bool {
pa, pb := uf.find(a), uf.find(b)
if pa == pb {
return false
}
if uf.size[pa] > uf.size[pb] {
uf.p[pb] = pa
uf.size[pa] += uf.size[pb]
} else {
uf.p[pa] = pb
uf.size[pb] += uf.size[pa]
}
return true
}
func latestDayToCross(row int, col int, cells [][]int) int {
mn := len(cells)
uf := newUnionFind(mn + 2)
s, t := mn, mn+1
g := make([][]int, row)
for i := range g {
g[i] = make([]int, col)
for j := range g[i] {
g[i][j] = 1
}
}
dirs := [5]int{-1, 0, 1, 0, -1}
for i := mn - 1; ; i-- {
x, y := cells[i][0]-1, cells[i][1]-1
g[x][y] = 0
for j := 0; j < 4; j++ {
nx, ny := x+dirs[j], y+dirs[j+1]
if nx >= 0 && nx < row && ny >= 0 && ny < col && g[nx][ny] == 0 {
uf.union(x*col+y, nx*col+ny)
}
}
if x == 0 {
uf.union(s, x*col+y)
}
if x == row-1 {
uf.union(t, x*col+y)
}
if uf.find(s) == uf.find(t) {
return i
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59 | class UnionFind {
p: number[];
size: number[];
constructor(n: number) {
this.p = Array(n)
.fill(0)
.map((_, i) => i);
this.size = Array(n).fill(1);
}
find(x: number): number {
if (this.p[x] !== x) {
this.p[x] = this.find(this.p[x]);
}
return this.p[x];
}
union(a: number, b: number): boolean {
const [pa, pb] = [this.find(a), this.find(b)];
if (pa === pb) {
return false;
}
if (this.size[pa] > this.size[pb]) {
this.p[pb] = pa;
this.size[pa] += this.size[pb];
} else {
this.p[pa] = pb;
this.size[pb] += this.size[pa];
}
return true;
}
}
function latestDayToCross(row: number, col: number, cells: number[][]): number {
const mn = cells.length;
const uf = new UnionFind(row * col + 2);
const [s, t] = [mn, mn + 1];
const g: number[][] = Array.from({ length: row }, () => Array(col).fill(1));
const dirs: number[] = [-1, 0, 1, 0, -1];
for (let i = mn - 1; ; --i) {
const [x, y] = [cells[i][0] - 1, cells[i][1] - 1];
g[x][y] = 0;
for (let j = 0; j < 4; ++j) {
const [nx, ny] = [x + dirs[j], y + dirs[j + 1]];
if (nx >= 0 && nx < row && ny >= 0 && ny < col && g[nx][ny] === 0) {
uf.union(x * col + y, nx * col + ny);
}
}
if (x === 0) {
uf.union(s, y);
}
if (x === row - 1) {
uf.union(t, x * col + y);
}
if (uf.find(s) === uf.find(t)) {
return i;
}
}
}
|





