


题目描述
给你一个 m x n 的整数矩阵 points (下标从 0 开始)。一开始你的得分为 0 ,你想最大化从矩阵中得到的分数。
你的得分方式为:每一行 中选取一个格子,选中坐标为 (r, c) 的格子会给你的总得分 增加 points[r][c] 。
然而,相邻行之间被选中的格子如果隔得太远,你会失去一些得分。对于相邻行 r 和 r + 1 (其中 0 <= r < m - 1),选中坐标为 (r, c1) 和 (r + 1, c2) 的格子,你的总得分 减少 abs(c1 - c2) 。
请你返回你能得到的 最大 得分。
abs(x) 定义为:
- 如果
x >= 0 ,那么值为 x 。
- 如果
x < 0 ,那么值为 -x 。
示例 1:
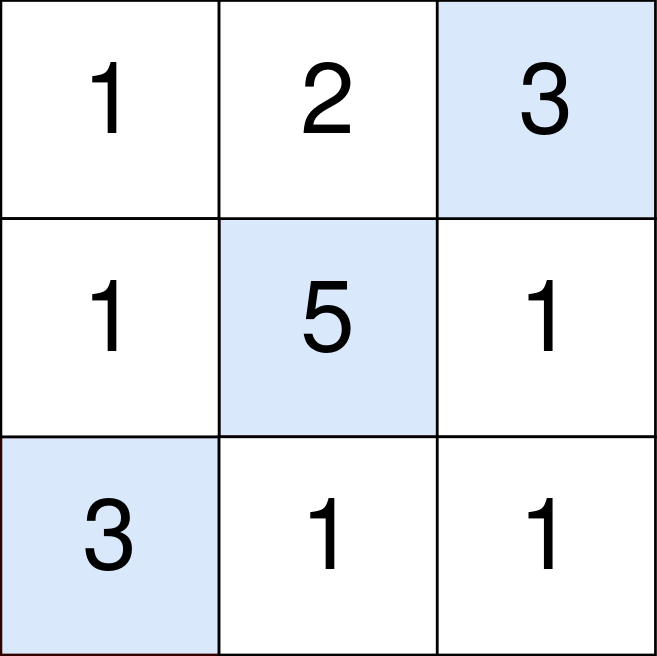
输入:points = [[1,2,3],[1,5,1],[3,1,1]]
输出:9
解释:
蓝色格子是最优方案选中的格子,坐标分别为 (0, 2),(1, 1) 和 (2, 0) 。
你的总得分增加 3 + 5 + 3 = 11 。
但是你的总得分需要扣除 abs(2 - 1) + abs(1 - 0) = 2 。
你的最终得分为 11 - 2 = 9 。
示例 2:
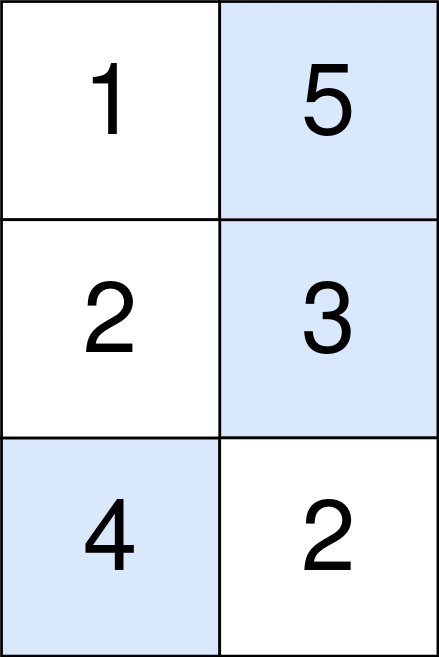
输入:points = [[1,5],[2,3],[4,2]]
输出:11
解释:
蓝色格子是最优方案选中的格子,坐标分别为 (0, 1),(1, 1) 和 (2, 0) 。
你的总得分增加 5 + 3 + 4 = 12 。
但是你的总得分需要扣除 abs(1 - 1) + abs(1 - 0) = 1 。
你的最终得分为 12 - 1 = 11 。
提示:
m == points.lengthn == points[r].length1 <= m, n <= 1051 <= m * n <= 1050 <= points[r][c] <= 105
解法
方法一:动态规划
我们定义 \(f[i][j]\) 表示选取前 \(i-1\) 行,并且第 \(i-1\) 行选择第 \(j\) 列的格子时的最大得分。初始时 \(f[0][j] = points[0][j]\)。
对于 \(i > 0\) 的情况,对于 \(f[i][j]\),我们考虑是从上一行的哪一列转移过来的,记上一行选择的列为 \(k\),那么有:
\[
f[i][j]=
\begin{cases}
\max(f[i - 1][k] + k - j + points[i][j]), & 0 \le k < j \\
\max(f[i - 1][k] - k + j + points[i][j]), & j < k < n
\end{cases}
\]
其中 \(n\) 表示列数。答案为 \(\max\limits_{0 \le j < n} f[m - 1][j]\)。
我们注意到 \(f[i]\) 的值只跟 \(f[i-1]\) 的值有关,因此我们可以使用滚动数组优化空间复杂度。
时间复杂度 \(O(m \times n)\),空间复杂度 \(O(n)\)。其中 \(m\) 和 \(n\) 分别是矩阵的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | class Solution:
def maxPoints(self, points: List[List[int]]) -> int:
n = len(points[0])
f = points[0][:]
for p in points[1:]:
g = [0] * n
lmx = -inf
for j in range(n):
lmx = max(lmx, f[j] + j)
g[j] = max(g[j], p[j] + lmx - j)
rmx = -inf
for j in range(n - 1, -1, -1):
rmx = max(rmx, f[j] - j)
g[j] = max(g[j], p[j] + rmx + j)
f = g
return max(f)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 | class Solution {
public long maxPoints(int[][] points) {
int n = points[0].length;
long[] f = new long[n];
final long inf = 1L << 60;
for (int[] p : points) {
long[] g = new long[n];
long lmx = -inf, rmx = -inf;
for (int j = 0; j < n; ++j) {
lmx = Math.max(lmx, f[j] + j);
g[j] = Math.max(g[j], p[j] + lmx - j);
}
for (int j = n - 1; j >= 0; --j) {
rmx = Math.max(rmx, f[j] - j);
g[j] = Math.max(g[j], p[j] + rmx + j);
}
f = g;
}
long ans = 0;
for (long x : f) {
ans = Math.max(ans, x);
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | class Solution {
public:
long long maxPoints(vector<vector<int>>& points) {
using ll = long long;
int n = points[0].size();
vector<ll> f(n);
const ll inf = 1e18;
for (auto& p : points) {
vector<ll> g(n);
ll lmx = -inf, rmx = -inf;
for (int j = 0; j < n; ++j) {
lmx = max(lmx, f[j] + j);
g[j] = max(g[j], p[j] + lmx - j);
}
for (int j = n - 1; ~j; --j) {
rmx = max(rmx, f[j] - j);
g[j] = max(g[j], p[j] + rmx + j);
}
f = move(g);
}
return *max_element(f.begin(), f.end());
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | func maxPoints(points [][]int) int64 {
n := len(points[0])
const inf int64 = 1e18
f := make([]int64, n)
for _, p := range points {
g := make([]int64, n)
lmx, rmx := -inf, -inf
for j := range p {
lmx = max(lmx, f[j]+int64(j))
g[j] = max(g[j], int64(p[j])+lmx-int64(j))
}
for j := n - 1; j >= 0; j-- {
rmx = max(rmx, f[j]-int64(j))
g[j] = max(g[j], int64(p[j])+rmx+int64(j))
}
f = g
}
return slices.Max(f)
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | function maxPoints(points: number[][]): number {
const n = points[0].length;
const f: number[] = new Array(n).fill(0);
for (const p of points) {
const g: number[] = new Array(n).fill(0);
let lmx = -Infinity;
let rmx = -Infinity;
for (let j = 0; j < n; ++j) {
lmx = Math.max(lmx, f[j] + j);
g[j] = Math.max(g[j], p[j] + lmx - j);
}
for (let j = n - 1; ~j; --j) {
rmx = Math.max(rmx, f[j] - j);
g[j] = Math.max(g[j], p[j] + rmx + j);
}
f.splice(0, n, ...g);
}
return Math.max(...f);
}
|




