1916. 统计为蚁群构筑房间的不同顺序

题目描述

你是一只蚂蚁，负责为蚁群构筑 n 间编号从 0 到 n-1 的新房间。给你一个 下标从 0 开始 且长度为 n 的整数数组 prevRoom 作为扩建计划。其中，prevRoom[i] 表示在构筑房间 i 之前，你必须先构筑房间 prevRoom[i] ，并且这两个房间必须 直接 相连。房间 0 已经构筑完成，所以 prevRoom[0] = -1 。扩建计划中还有一条硬性要求，在完成所有房间的构筑之后，从房间 0 可以访问到每个房间。

你一次只能构筑 一个 房间。你可以在 已经构筑好的 房间之间自由穿行，只要这些房间是 相连的 。如果房间 prevRoom[i] 已经构筑完成，那么你就可以构筑房间 i。

返回你构筑所有房间的 不同顺序的数目 。由于答案可能很大，请返回对 109 + 7 取余 的结果。

 

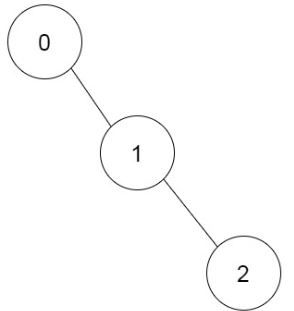
示例 1：

输入：prevRoom = [-1,0,1]
输出：1
解释：仅有一种方案可以完成所有房间的构筑：0 → 1 → 2

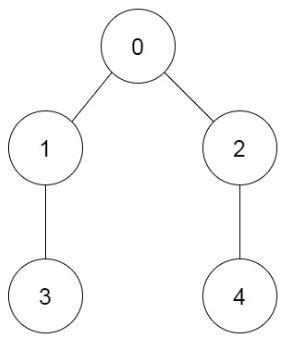
示例 2：

输入：prevRoom = [-1,0,0,1,2]
输出：6
解释：
有 6 种不同顺序：
0 → 1 → 3 → 2 → 4
0 → 2 → 4 → 1 → 3
0 → 1 → 2 → 3 → 4
0 → 1 → 2 → 4 → 3
0 → 2 → 1 → 3 → 4
0 → 2 → 1 → 4 → 3

 

提示：

• n == prevRoom.length
• 2 <= n <= 105
• prevRoom[0] == -1
• 对于所有的 1 <= i < n ，都有 0 <= prevRoom[i] < n
• 题目保证所有房间都构筑完成后，从房间 0 可以访问到每个房间

解法

方法一

Python3JavaC++Go

评论