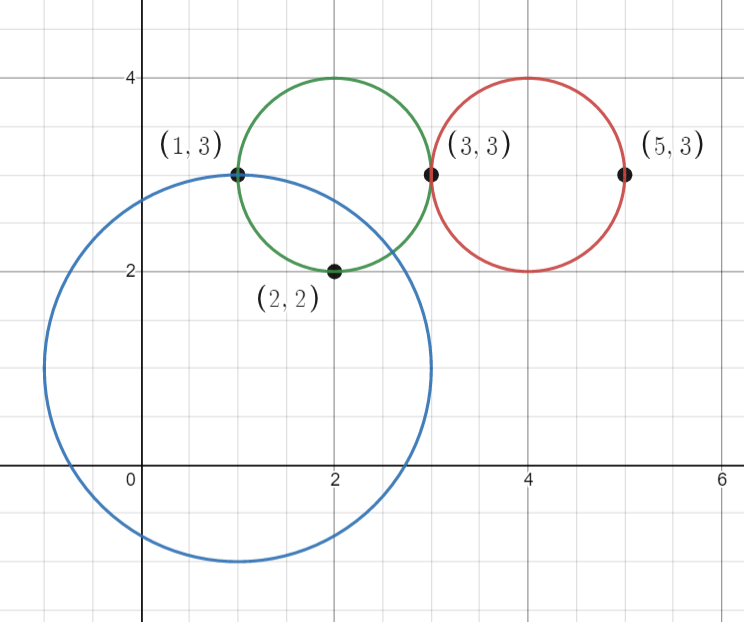几何
数学
数组
题目描述
给你一个数组 points ,其中 points[i] = [xi , yi ] ,表示第 i 个点在二维平面上的坐标。多个点可能会有 相同 的坐标。
同时给你一个数组 queries ,其中 queries[j] = [xj , yj , rj ] ,表示一个圆心在 (xj , yj ) 且半径为 rj 的圆。
对于每一个查询 queries[j] ,计算在第 j 个圆 内 点的数目。如果一个点在圆的 边界上 ,我们同样认为它在圆 内 。
请你返回一个数组 answer ,其中 answer[j]是第 j 个查询的答案。
示例 1:
输入: points = [[1,3],[3,3],[5,3],[2,2]], queries = [[2,3,1],[4,3,1],[1,1,2]]
输出: [3,2,2]
解释: 所有的点和圆如上图所示。
queries[0] 是绿色的圆,queries[1] 是红色的圆,queries[2] 是蓝色的圆。
示例 2:
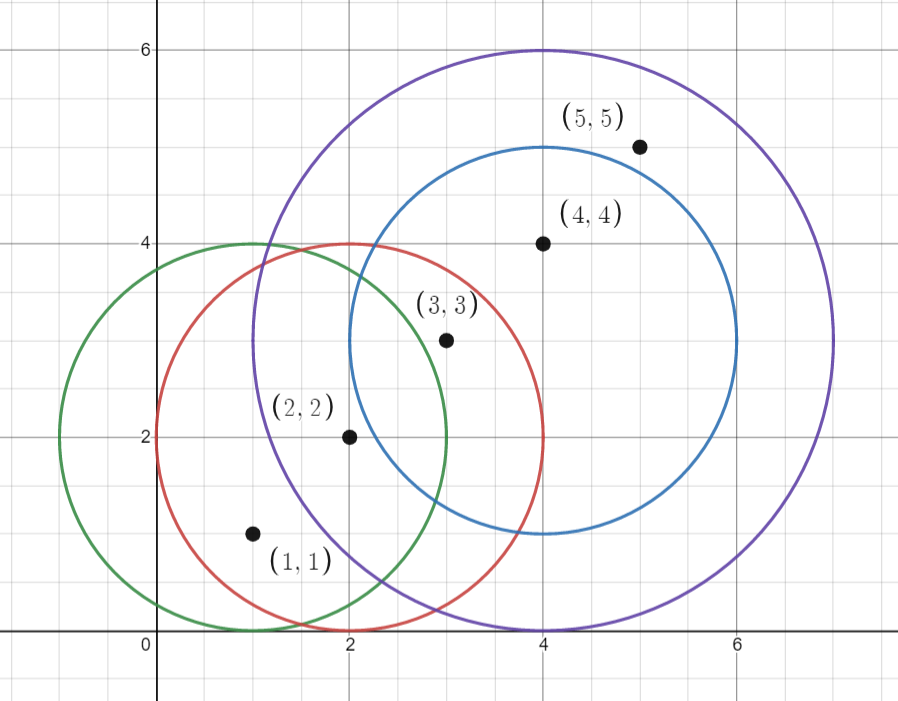
输入: points = [[1,1],[2,2],[3,3],[4,4],[5,5]], queries = [[1,2,2],[2,2,2],[4,3,2],[4,3,3]]
输出: [2,3,2,4]
解释: 所有的点和圆如上图所示。
queries[0] 是绿色的圆,queries[1] 是红色的圆,queries[2] 是蓝色的圆,queries[3] 是紫色的圆。
提示:
1 <= points.length <= 500points[i].length == 20 <= xi , yi <= 5001 <= queries.length <= 500queries[j].length == 30 <= xj , yj <= 5001 <= rj <= 500所有的坐标都是整数。
解法
方法一:枚举
枚举所有的圆点 \((x, y, r)\) ,对于每个圆点,计算在圆内的点的个数,即可得到答案。
时间复杂度 \(O(m \times n)\) ,其中 \(m\) 和 \(n\) 分别为数组 queries 的长度和 points 的长度。忽略答案的空间消耗,空间复杂度 \(O(1)\) 。
Python3 Java C++ Go TypeScript Rust C
1
2
3
4
5
6
7
8
9
10
11
12 class Solution :
def countPoints (
self , points : List [ List [ int ]], queries : List [ List [ int ]]
) -> List [ int ]:
ans = []
for x , y , r in queries :
cnt = 0
for i , j in points :
dx , dy = i - x , j - y
cnt += dx * dx + dy * dy <= r * r
ans . append ( cnt )
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 class Solution {
public int [] countPoints ( int [][] points , int [][] queries ) {
int m = queries . length ;
int [] ans = new int [ m ] ;
for ( int k = 0 ; k < m ; ++ k ) {
int x = queries [ k ][ 0 ] , y = queries [ k ][ 1 ] , r = queries [ k ][ 2 ] ;
for ( var p : points ) {
int i = p [ 0 ] , j = p [ 1 ] ;
int dx = i - x , dy = j - y ;
if ( dx * dx + dy * dy <= r * r ) {
++ ans [ k ] ;
}
}
}
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 class Solution {
public :
vector < int > countPoints ( vector < vector < int >>& points , vector < vector < int >>& queries ) {
vector < int > ans ;
for ( auto & q : queries ) {
int x = q [ 0 ], y = q [ 1 ], r = q [ 2 ];
int cnt = 0 ;
for ( auto & p : points ) {
int i = p [ 0 ], j = p [ 1 ];
int dx = i - x , dy = j - y ;
cnt += dx * dx + dy * dy <= r * r ;
}
ans . emplace_back ( cnt );
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 func countPoints ( points [][] int , queries [][] int ) ( ans [] int ) {
for _ , q := range queries {
x , y , r := q [ 0 ], q [ 1 ], q [ 2 ]
cnt := 0
for _ , p := range points {
i , j := p [ 0 ], p [ 1 ]
dx , dy := i - x , j - y
if dx * dx + dy * dy <= r * r {
cnt ++
}
}
ans = append ( ans , cnt )
}
return
}
function countPoints ( points : number [][], queries : number [][]) : number [] {
return queries . map (([ cx , cy , r ]) => {
let res = 0 ;
for ( const [ px , py ] of points ) {
if ( Math . sqrt (( cx - px ) ** 2 + ( cy - py ) ** 2 ) <= r ) {
res ++ ;
}
}
return res ;
});
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 impl Solution {
pub fn count_points ( points : Vec < Vec < i32 >> , queries : Vec < Vec < i32 >> ) -> Vec < i32 > {
queries
. iter ()
. map ( | v | {
let cx = v [ 0 ];
let cy = v [ 1 ];
let r = v [ 2 ]. pow ( 2 );
let mut count = 0 ;
for p in points . iter () {
if ( p [ 0 ] - cx ). pow ( 2 ) + ( p [ 1 ] - cy ). pow ( 2 ) <= r {
count += 1 ;
}
}
count
})
. collect ()
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 /**
* Note: The returned array must be malloced, assume caller calls free().
*/
int * countPoints ( int ** points , int pointsSize , int * pointsColSize , int ** queries , int queriesSize , int * queriesColSize ,
int * returnSize ) {
int * ans = malloc ( sizeof ( int ) * queriesSize );
for ( int i = 0 ; i < queriesSize ; i ++ ) {
int cx = queries [ i ][ 0 ];
int cy = queries [ i ][ 1 ];
int r = queries [ i ][ 2 ];
int count = 0 ;
for ( int j = 0 ; j < pointsSize ; j ++ ) {
if ( sqrt ( pow ( points [ j ][ 0 ] - cx , 2 ) + pow ( points [ j ][ 1 ] - cy , 2 )) <= r ) {
count ++ ;
}
}
ans [ i ] = count ;
}
* returnSize = queriesSize ;
return ans ;
}