跳转至

1824. 最少侧跳次数

题目描述

给你一个长度为 n 的 3 跑道道路 ，它总共包含 n + 1 个 点 ，编号为 0 到 n 。一只青蛙从 0 号点第二条跑道 出发 ，它想要跳到点 n 处。然而道路上可能有一些障碍。

给你一个长度为 n + 1 的数组 obstacles ，其中 obstacles[i] （取值范围从 0 到 3）表示在点 i 处的 obstacles[i] 跑道上有一个障碍。如果 obstacles[i] == 0 ，那么点 i 处没有障碍。任何一个点的三条跑道中 最多有一个 障碍。

  • 比方说，如果 obstacles[2] == 1 ，那么说明在点 2 处跑道 1 有障碍。

这只青蛙从点 i 跳到点 i + 1 且跑道不变的前提是点 i + 1 的同一跑道上没有障碍。为了躲避障碍，这只青蛙也可以在 同一个 点处 侧跳 到 另外一条 跑道（这两条跑道可以不相邻），但前提是跳过去的跑道该点处没有障碍。

  • 比方说，这只青蛙可以从点 3 处的跑道 3 跳到点 3 处的跑道 1 。

这只青蛙从点 0 处跑道 2 出发，并想到达点 n 处的 任一跑道 ，请你返回 最少侧跳次数 。

注意：点 0 处和点 n 处的任一跑道都不会有障碍。

 

示例 1：

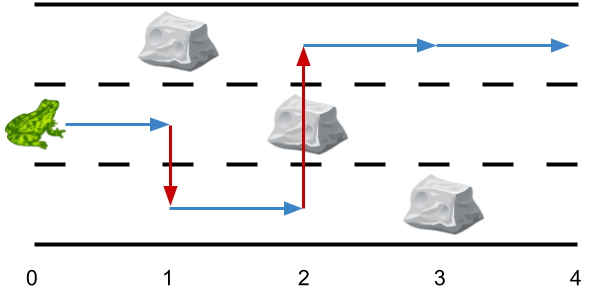
输入：obstacles = [0,1,2,3,0]
输出：2 
解释：最优方案如上图箭头所示。总共有 2 次侧跳（红色箭头）。
注意，这只青蛙只有当侧跳时才可以跳过障碍（如上图点 2 处所示）。

示例 2：

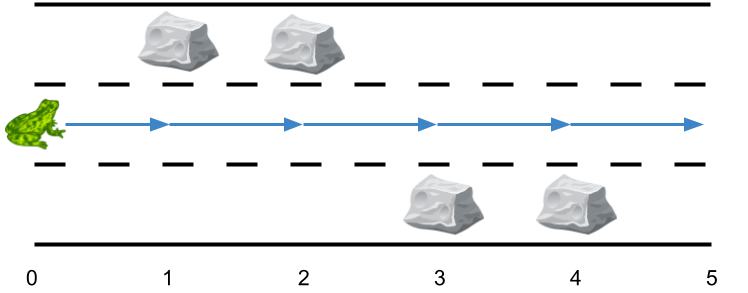
输入：obstacles = [0,1,1,3,3,0]
输出：0
解释：跑道 2 没有任何障碍，所以不需要任何侧跳。

示例 3：

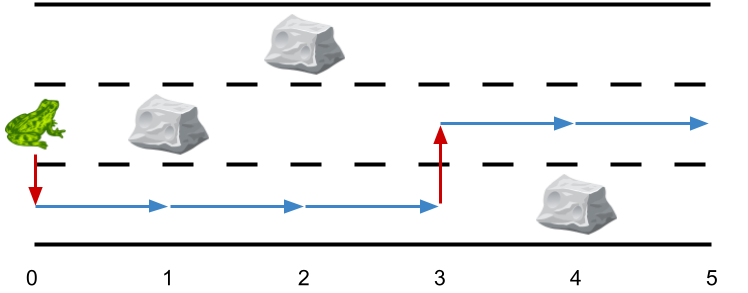
输入：obstacles = [0,2,1,0,3,0]
输出：2
解释：最优方案如上图所示。总共有 2 次侧跳。

 

提示：

  • obstacles.length == n + 1
  • 1 <= n <= 5 * 105
  • 0 <= obstacles[i] <= 3
  • obstacles[0] == obstacles[n] == 0

解法

方法一：动态规划

我们定义 $f[i][j]$ 表示青蛙到达第 $i$ 个点，且处于第 $j$ 条跑道（下标从 $0$ 开始）的最小侧跳次数。

注意到青蛙起始位置处于第 $2$ 条跑道（题目这里下标从 $1$ 开始），因此 $f[0][1]$ 的值为 $0$，而 $f[0][0]$ 和 $f[0][2]$ 的值均为 $1$。答案为 $min(f[n][0], f[n][1], f[n][2])$

对于 $i$ 从 $1$ 到 $n$ 的每个位置，我们可以枚举青蛙当前所处的跑道 $j$，如果 $obstacles[i] = j + 1$，说明第 $j$ 条跑道上有障碍，此时 $f[i][j]$ 的值为正无穷；否则，青蛙可以选择不跳跃，此时 $f[i][j]$ 的值为 $f[i - 1][j]$，或者青蛙可以从其它跑道侧跳过来，此时 $f[i][j] = min(f[i][j], min(f[i][0], f[i][1], f[i][2]) + 1)$。

在代码实现上，我们可以将第一维空间优化掉，只用一个长度为 $3$ 的数组 $f$ 来维护。

时间复杂度 $O(n)$，其中 $n$ 为数组 $obstacles$ 的长度。空间复杂度 $O(1)$。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution:
    def minSideJumps(self, obstacles: List[int]) -> int:
        f = [1, 0, 1]
        for v in obstacles[1:]:
            for j in range(3):
                if v == j + 1:
                    f[j] = inf
                    break
            x = min(f) + 1
            for j in range(3):
                if v != j + 1:
                    f[j] = min(f[j], x)
        return min(f)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int minSideJumps(int[] obstacles) {
        final int inf = 1 << 30;
        int[] f = {1, 0, 1};
        for (int i = 1; i < obstacles.length; ++i) {
            for (int j = 0; j < 3; ++j) {
                if (obstacles[i] == j + 1) {
                    f[j] = inf;
                    break;
                }
            }
            int x = Math.min(f[0], Math.min(f[1], f[2])) + 1;
            for (int j = 0; j < 3; ++j) {
                if (obstacles[i] != j + 1) {
                    f[j] = Math.min(f[j], x);
                }
            }
        }
        return Math.min(f[0], Math.min(f[1], f[2]));
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int minSideJumps(vector<int>& obstacles) {
        const int inf = 1 << 30;
        int f[3] = {1, 0, 1};
        for (int i = 1; i < obstacles.size(); ++i) {
            for (int j = 0; j < 3; ++j) {
                if (obstacles[i] == j + 1) {
                    f[j] = inf;
                    break;
                }
            }
            int x = min({f[0], f[1], f[2]}) + 1;
            for (int j = 0; j < 3; ++j) {
                if (obstacles[i] != j + 1) {
                    f[j] = min(f[j], x);
                }
            }
        }
        return min({f[0], f[1], f[2]});
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
func minSideJumps(obstacles []int) int {
    f := [3]int{1, 0, 1}
    const inf = 1 << 30
    for _, v := range obstacles[1:] {
        for j := 0; j < 3; j++ {
            if v == j+1 {
                f[j] = inf
                break
            }
        }
        x := min(f[0], min(f[1], f[2])) + 1
        for j := 0; j < 3; j++ {
            if v != j+1 {
                f[j] = min(f[j], x)
            }
        }
    }
    return min(f[0], min(f[1], f[2]))
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
function minSideJumps(obstacles: number[]): number {
    const inf = 1 << 30;
    const f = [1, 0, 1];
    for (let i = 1; i < obstacles.length; ++i) {
        for (let j = 0; j < 3; ++j) {
            if (obstacles[i] == j + 1) {
                f[j] = inf;
                break;
            }
        }
        const x = Math.min(...f) + 1;
        for (let j = 0; j < 3; ++j) {
            if (obstacles[i] != j + 1) {
                f[j] = Math.min(f[j], x);
            }
        }
    }
    return Math.min(...f);
}

评论