广度优先搜索
数组
矩阵
题目描述
给你一个大小为 m x n 的整数矩阵 isWater ,它代表了一个由 陆地 和 水域 单元格组成的地图。
如果 isWater[i][j] == 0 ,格子 (i, j) 是一个 陆地 格子。
如果 isWater[i][j] == 1 ,格子 (i, j) 是一个 水域 格子。
你需要按照如下规则给每个单元格安排高度:
每个格子的高度都必须是非负的。
如果一个格子是 水域 ,那么它的高度必须为 0 。
任意相邻的格子高度差 至多 为 1 。当两个格子在正东、南、西、北方向上相互紧挨着,就称它们为相邻的格子。(也就是说它们有一条公共边)
找到一种安排高度的方案,使得矩阵中的最高高度值 最大 。
请你返回一个大小为 m x n 的整数矩阵 height ,其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法,请返回 任意一个 。
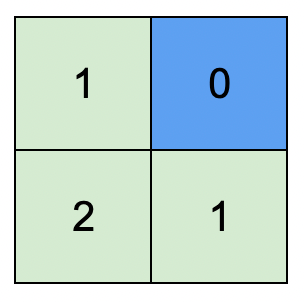
示例 1:
输入: isWater = [[0,1],[0,0]]
输出: [[1,0],[2,1]]
解释: 上图展示了给各个格子安排的高度。
蓝色格子是水域格,绿色格子是陆地格。
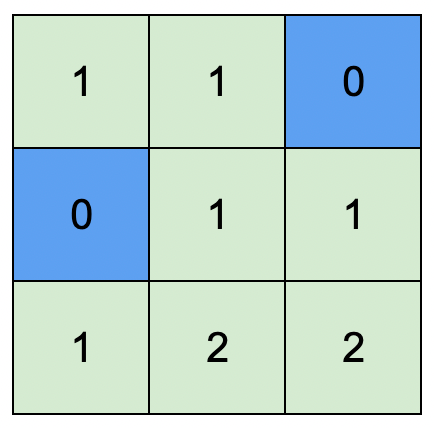
示例 2:
输入: isWater = [[0,0,1],[1,0,0],[0,0,0]]
输出: [[1,1,0],[0,1,1],[1,2,2]]
解释: 所有安排方案中,最高可行高度为 2 。
任意安排方案中,只要最高高度为 2 且符合上述规则的,都为可行方案。
提示:
m == isWater.lengthn == isWater[i].length1 <= m, n <= 1000isWater[i][j] 要么是 0 ,要么是 1 。至少有 1 个水域格子。
注意: 本题与 542 题相同。
解法
方法一:BFS
根据题目描述,水域的高度必须是 \(0\) ,而任意相邻格子的高度差至多为 \(1\) 。因此,我们可以从所有水域格子出发,用 BFS 搜索相邻且未访问过的格子,将其高度置为当前格子的高度再加一。
最后返回结果矩阵即可。
时间复杂度 \(O(m \times n)\) ,空间复杂度 \(O(m \times n)\) 。其中 \(m\) 和 \(n\) 分别是整数矩阵 isWater 的行数和列数。
Python3 Java C++ Go TypeScript Rust
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 class Solution :
def highestPeak ( self , isWater : List [ List [ int ]]) -> List [ List [ int ]]:
m , n = len ( isWater ), len ( isWater [ 0 ])
ans = [[ - 1 ] * n for _ in range ( m )]
q = deque ()
for i , row in enumerate ( isWater ):
for j , v in enumerate ( row ):
if v :
q . append (( i , j ))
ans [ i ][ j ] = 0
while q :
i , j = q . popleft ()
for a , b in pairwise (( - 1 , 0 , 1 , 0 , - 1 )):
x , y = i + a , j + b
if 0 <= x < m and 0 <= y < n and ans [ x ][ y ] == - 1 :
ans [ x ][ y ] = ans [ i ][ j ] + 1
q . append (( x , y ))
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 class Solution {
public int [][] highestPeak ( int [][] isWater ) {
int m = isWater . length , n = isWater [ 0 ] . length ;
int [][] ans = new int [ m ][ n ] ;
Deque < int []> q = new ArrayDeque <> ();
for ( int i = 0 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
ans [ i ][ j ] = isWater [ i ][ j ] - 1 ;
if ( ans [ i ][ j ] == 0 ) {
q . offer ( new int [] { i , j });
}
}
}
int [] dirs = { - 1 , 0 , 1 , 0 , - 1 };
while ( ! q . isEmpty ()) {
var p = q . poll ();
int i = p [ 0 ] , j = p [ 1 ] ;
for ( int k = 0 ; k < 4 ; ++ k ) {
int x = i + dirs [ k ] , y = j + dirs [ k + 1 ] ;
if ( x >= 0 && x < m && y >= 0 && y < n && ans [ x ][ y ] == - 1 ) {
ans [ x ][ y ] = ans [ i ][ j ] + 1 ;
q . offer ( new int [] { x , y });
}
}
}
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 class Solution {
public :
const int dirs [ 5 ] = { -1 , 0 , 1 , 0 , -1 };
vector < vector < int >> highestPeak ( vector < vector < int >>& isWater ) {
int m = isWater . size (), n = isWater [ 0 ]. size ();
vector < vector < int >> ans ( m , vector < int > ( n ));
queue < pair < int , int >> q ;
for ( int i = 0 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
ans [ i ][ j ] = isWater [ i ][ j ] - 1 ;
if ( ans [ i ][ j ] == 0 ) {
q . emplace ( i , j );
}
}
}
while ( ! q . empty ()) {
auto [ i , j ] = q . front ();
q . pop ();
for ( int k = 0 ; k < 4 ; ++ k ) {
int x = i + dirs [ k ], y = j + dirs [ k + 1 ];
if ( x >= 0 && x < m && y >= 0 && y < n && ans [ x ][ y ] == -1 ) {
ans [ x ][ y ] = ans [ i ][ j ] + 1 ;
q . emplace ( x , y );
}
}
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 func highestPeak ( isWater [][] int ) [][] int {
m , n := len ( isWater ), len ( isWater [ 0 ])
ans := make ([][] int , m )
type pair struct { i , j int }
q := [] pair {}
for i , row := range isWater {
ans [ i ] = make ([] int , n )
for j , v := range row {
ans [ i ][ j ] = v - 1
if v == 1 {
q = append ( q , pair { i , j })
}
}
}
dirs := [] int { - 1 , 0 , 1 , 0 , - 1 }
for len ( q ) > 0 {
p := q [ 0 ]
q = q [ 1 :]
i , j := p . i , p . j
for k := 0 ; k < 4 ; k ++ {
x , y := i + dirs [ k ], j + dirs [ k + 1 ]
if x >= 0 && x < m && y >= 0 && y < n && ans [ x ][ y ] == - 1 {
ans [ x ][ y ] = ans [ i ][ j ] + 1
q = append ( q , pair { x , y })
}
}
}
return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 function highestPeak ( isWater : number [][]) : number [][] {
const m = isWater . length ;
const n = isWater [ 0 ]. length ;
let ans : number [][] = [];
let q : number [][] = [];
for ( let i = 0 ; i < m ; ++ i ) {
ans . push ( new Array ( n ). fill ( - 1 ));
for ( let j = 0 ; j < n ; ++ j ) {
if ( isWater [ i ][ j ]) {
q . push ([ i , j ]);
ans [ i ][ j ] = 0 ;
}
}
}
const dirs = [ - 1 , 0 , 1 , 0 , - 1 ];
while ( q . length ) {
let tq : number [][] = [];
for ( const [ i , j ] of q ) {
for ( let k = 0 ; k < 4 ; k ++ ) {
const [ x , y ] = [ i + dirs [ k ], j + dirs [ k + 1 ]];
if ( x >= 0 && x < m && y >= 0 && y < n && ans [ x ][ y ] == - 1 ) {
tq . push ([ x , y ]);
ans [ x ][ y ] = ans [ i ][ j ] + 1 ;
}
}
}
q = tq ;
}
return ans ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49 use std :: collections :: VecDeque ;
impl Solution {
#[allow(dead_code)]
pub fn highest_peak ( is_water : Vec < Vec < i32 >> ) -> Vec < Vec < i32 >> {
let n = is_water . len ();
let m = is_water [ 0 ]. len ();
let mut ret_vec = vec! [ vec! [ - 1 ; m ]; n ];
let mut q : VecDeque < ( usize , usize ) > = VecDeque :: new ();
let vis_pair : Vec < ( i32 , i32 ) > = vec! [( - 1 , 0 ), ( 1 , 0 ), ( 0 , - 1 ), ( 0 , 1 )];
// Initialize the return vector
for i in 0 .. n {
for j in 0 .. m {
if is_water [ i ][ j ] == 1 {
// This cell is water, the height of which must be 0
ret_vec [ i ][ j ] = 0 ;
q . push_back (( i , j ));
}
}
}
while ! q . is_empty () {
// Get the front X-Y Coordinates
let ( x , y ) = q . front (). unwrap (). clone ();
q . pop_front ();
// Traverse through the vis pair
for d in & vis_pair {
let ( dx , dy ) = * d ;
if Self :: check_bounds (( x as i32 ) + dx , ( y as i32 ) + dy , n as i32 , m as i32 ) {
if ret_vec [(( x as i32 ) + dx ) as usize ][(( y as i32 ) + dy ) as usize ] == - 1 {
// This cell hasn't been visited, update its height
ret_vec [(( x as i32 ) + dx ) as usize ][(( y as i32 ) + dy ) as usize ] =
ret_vec [ x ][ y ] + 1 ;
// Enqueue the current cell
q . push_back (((( x as i32 ) + dx ) as usize , (( y as i32 ) + dy ) as usize ));
}
}
}
}
ret_vec
}
#[allow(dead_code)]
fn check_bounds ( i : i32 , j : i32 , n : i32 , m : i32 ) -> bool {
i >= 0 && i < n && j >= 0 && j < m
}
}
方法二
Python3 Java C++ Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 class Solution :
def highestPeak ( self , isWater : List [ List [ int ]]) -> List [ List [ int ]]:
m , n = len ( isWater ), len ( isWater [ 0 ])
ans = [[ - 1 ] * n for _ in range ( m )]
q = deque ()
for i , row in enumerate ( isWater ):
for j , v in enumerate ( row ):
if v :
q . append (( i , j ))
ans [ i ][ j ] = 0
while q :
for _ in range ( len ( q )):
i , j = q . popleft ()
for a , b in pairwise (( - 1 , 0 , 1 , 0 , - 1 )):
x , y = i + a , j + b
if 0 <= x < m and 0 <= y < n and ans [ x ][ y ] == - 1 :
ans [ x ][ y ] = ans [ i ][ j ] + 1
q . append (( x , y ))
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 class Solution {
public int [][] highestPeak ( int [][] isWater ) {
int m = isWater . length , n = isWater [ 0 ] . length ;
int [][] ans = new int [ m ][ n ] ;
Deque < int []> q = new ArrayDeque <> ();
for ( int i = 0 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
ans [ i ][ j ] = isWater [ i ][ j ] - 1 ;
if ( ans [ i ][ j ] == 0 ) {
q . offer ( new int [] { i , j });
}
}
}
int [] dirs = { - 1 , 0 , 1 , 0 , - 1 };
while ( ! q . isEmpty ()) {
for ( int t = q . size (); t > 0 ; -- t ) {
var p = q . poll ();
int i = p [ 0 ] , j = p [ 1 ] ;
for ( int k = 0 ; k < 4 ; ++ k ) {
int x = i + dirs [ k ] , y = j + dirs [ k + 1 ] ;
if ( x >= 0 && x < m && y >= 0 && y < n && ans [ x ][ y ] == - 1 ) {
ans [ x ][ y ] = ans [ i ][ j ] + 1 ;
q . offer ( new int [] { x , y });
}
}
}
}
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 class Solution {
public :
const int dirs [ 5 ] = { -1 , 0 , 1 , 0 , -1 };
vector < vector < int >> highestPeak ( vector < vector < int >>& isWater ) {
int m = isWater . size (), n = isWater [ 0 ]. size ();
vector < vector < int >> ans ( m , vector < int > ( n ));
queue < pair < int , int >> q ;
for ( int i = 0 ; i < m ; ++ i ) {
for ( int j = 0 ; j < n ; ++ j ) {
ans [ i ][ j ] = isWater [ i ][ j ] - 1 ;
if ( ans [ i ][ j ] == 0 ) {
q . emplace ( i , j );
}
}
}
while ( ! q . empty ()) {
for ( int t = q . size (); t ; -- t ) {
auto [ i , j ] = q . front ();
q . pop ();
for ( int k = 0 ; k < 4 ; ++ k ) {
int x = i + dirs [ k ], y = j + dirs [ k + 1 ];
if ( x >= 0 && x < m && y >= 0 && y < n && ans [ x ][ y ] == -1 ) {
ans [ x ][ y ] = ans [ i ][ j ] + 1 ;
q . emplace ( x , y );
}
}
}
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 func highestPeak ( isWater [][] int ) [][] int {
m , n := len ( isWater ), len ( isWater [ 0 ])
ans := make ([][] int , m )
type pair struct { i , j int }
q := [] pair {}
for i , row := range isWater {
ans [ i ] = make ([] int , n )
for j , v := range row {
ans [ i ][ j ] = v - 1
if v == 1 {
q = append ( q , pair { i , j })
}
}
}
dirs := [] int { - 1 , 0 , 1 , 0 , - 1 }
for len ( q ) > 0 {
for t := len ( q ); t > 0 ; t -- {
p := q [ 0 ]
q = q [ 1 :]
i , j := p . i , p . j
for k := 0 ; k < 4 ; k ++ {
x , y := i + dirs [ k ], j + dirs [ k + 1 ]
if x >= 0 && x < m && y >= 0 && y < n && ans [ x ][ y ] == - 1 {
ans [ x ][ y ] = ans [ i ][ j ] + 1
q = append ( q , pair { x , y })
}
}
}
}
return ans
}