跳转至

1761. 一个图中连通三元组的最小度数

题目描述

给你一个无向图，整数 n 表示图中节点的数目，edges 数组表示图中的边，其中 edges[i] = [ui, vi] ，表示 ui 和 vi 之间有一条无向边。

一个 连通三元组 指的是 三个 节点组成的集合且这三个点之间 两两 有边。

连通三元组的度数 是所有满足此条件的边的数目：一个顶点在这个三元组内，而另一个顶点不在这个三元组内。

请你返回所有连通三元组中度数的 最小值 ，如果图中没有连通三元组，那么返回 -1 。

 

示例 1：

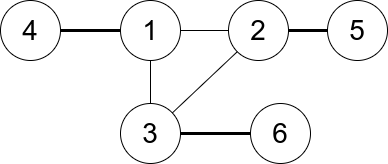
输入：n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
输出：3
解释：只有一个三元组 [1,2,3] 。构成度数的边在上图中已被加粗。

示例 2：

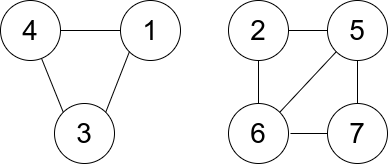
输入：n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
输出：0
解释：有 3 个三元组：
1) [1,4,3]，度数为 0 。
2) [2,5,6]，度数为 2 。
3) [5,6,7]，度数为 2 。

 

提示：

  • 2 <= n <= 400
  • edges[i].length == 2
  • 1 <= edges.length <= n * (n-1) / 2
  • 1 <= ui, vi <= n
  • ui != vi
  • 图中没有重复的边。

解法

方法一：暴力枚举

我们先将所有边存入邻接矩阵 $g$ 中，再将每个节点的度数存入数组 $deg$ 中。初始化答案 $ans=+\infty$。

然后枚举所有的三元组 $(i, j, k)$，其中 $i \lt j \lt k$，如果 $g[i][j] = g[j][k] = g[i][k] = 1$，则说明这三个节点构成了一个连通三元组，此时更新答案为 $ans = \min(ans, deg[i] + deg[j] + deg[k] - 6)$。

枚举完所有的三元组后，如果答案仍然为 $+\infty$，说明图中不存在连通三元组，返回 $-1$，否则返回答案。

时间复杂度 $O(n^3)$，空间复杂度 $O(n^2)$。其中 $n$ 为节点数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
class Solution:
    def minTrioDegree(self, n: int, edges: List[List[int]]) -> int:
        g = [[False] * n for _ in range(n)]
        deg = [0] * n
        for u, v in edges:
            u, v = u - 1, v - 1
            g[u][v] = g[v][u] = True
            deg[u] += 1
            deg[v] += 1
        ans = inf
        for i in range(n):
            for j in range(i + 1, n):
                if g[i][j]:
                    for k in range(j + 1, n):
                        if g[i][k] and g[j][k]:
                            ans = min(ans, deg[i] + deg[j] + deg[k] - 6)
        return -1 if ans == inf else ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int minTrioDegree(int n, int[][] edges) {
        boolean[][] g = new boolean[n][n];
        int[] deg = new int[n];
        for (var e : edges) {
            int u = e[0] - 1, v = e[1] - 1;
            g[u][v] = true;
            g[v][u] = true;
            ++deg[u];
            ++deg[v];
        }
        int ans = 1 << 30;
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                if (g[i][j]) {
                    for (int k = j + 1; k < n; ++k) {
                        if (g[i][k] && g[j][k]) {
                            ans = Math.min(ans, deg[i] + deg[j] + deg[k] - 6);
                        }
                    }
                }
            }
        }
        return ans == 1 << 30 ? -1 : ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    int minTrioDegree(int n, vector<vector<int>>& edges) {
        bool g[n][n];
        memset(g, 0, sizeof g);
        int deg[n];
        memset(deg, 0, sizeof deg);
        for (auto& e : edges) {
            int u = e[0] - 1, v = e[1] - 1;
            g[u][v] = g[v][u] = true;
            deg[u]++, deg[v]++;
        }
        int ans = INT_MAX;
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                if (g[i][j]) {
                    for (int k = j + 1; k < n; ++k) {
                        if (g[j][k] && g[i][k]) {
                            ans = min(ans, deg[i] + deg[j] + deg[k] - 6);
                        }
                    }
                }
            }
        }
        return ans == INT_MAX ? -1 : ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func minTrioDegree(n int, edges [][]int) int {
    g := make([][]bool, n)
    deg := make([]int, n)
    for i := range g {
        g[i] = make([]bool, n)
    }
    for _, e := range edges {
        u, v := e[0]-1, e[1]-1
        g[u][v], g[v][u] = true, true
        deg[u]++
        deg[v]++
    }
    ans := 1 << 30
    for i := 0; i < n; i++ {
        for j := i + 1; j < n; j++ {
            if g[i][j] {
                for k := j + 1; k < n; k++ {
                    if g[i][k] && g[j][k] {
                        ans = min(ans, deg[i]+deg[j]+deg[k]-6)
                    }
                }
            }
        }
    }
    if ans == 1<<30 {
        return -1
    }
    return ans
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
function minTrioDegree(n: number, edges: number[][]): number {
    const g = Array.from({ length: n }, () => Array(n).fill(false));
    const deg: number[] = Array(n).fill(0);
    for (let [u, v] of edges) {
        u--;
        v--;
        g[u][v] = g[v][u] = true;
        ++deg[u];
        ++deg[v];
    }
    let ans = Infinity;
    for (let i = 0; i < n; ++i) {
        for (let j = i + 1; j < n; ++j) {
            if (g[i][j]) {
                for (let k = j + 1; k < n; ++k) {
                    if (g[i][k] && g[j][k]) {
                        ans = Math.min(ans, deg[i] + deg[j] + deg[k] - 6);
                    }
                }
            }
        }
    }
    return ans === Infinity ? -1 : ans;
}

评论