二叉搜索树
二叉树
栈
树
设计
迭代器
题目描述
实现一个二叉搜索树迭代器类BSTIterator ,表示一个按中序遍历二叉搜索树(BST)的迭代器:
BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。boolean hasNext() 如果向指针右侧遍历存在数字,则返回 true ;否则返回 false 。int next()将指针向右移动,然后返回指针处的数字。
注意,指针初始化为一个不存在于 BST 中的数字,所以对 next() 的首次调用将返回 BST 中的最小元素。
你可以假设 next() 调用总是有效的,也就是说,当调用 next() 时,BST 的中序遍历中至少存在一个下一个数字。
示例:
输入
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
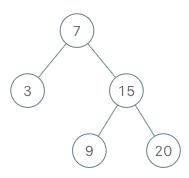
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
输出
[null, 3, 7, true, 9, true, 15, true, 20, false]
解释
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next(); // 返回 3
bSTIterator.next(); // 返回 7
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 9
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 15
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 20
bSTIterator.hasNext(); // 返回 False
提示:
树中节点的数目在范围 [1, 105 ] 内
0 <= Node.val <= 106 最多调用 105 次 hasNext 和 next 操作
进阶:
你可以设计一个满足下述条件的解决方案吗?next() 和 hasNext() 操作均摊时间复杂度为 O(1) ,并使用 O(h) 内存。其中 h 是树的高度。
解法
方法一:递归
初始化数据时,递归中序遍历,将二叉搜索树每个结点的值保存在列表 vals 中。用 cur 指针记录外部即将遍历的位置,初始化为 0。
调用 next() 时,返回 vals[cur],同时 cur 指针自增。调用 hasNext() 时,判断 cur 指针是否已经达到 len(vals) 个数,若是,说明已经遍历结束,返回 false,否则返回 true。
Python3 Java C++ Go TypeScript Rust JavaScript
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class BSTIterator :
def __init__ ( self , root : TreeNode ):
def inorder ( root ):
if root :
inorder ( root . left )
self . vals . append ( root . val )
inorder ( root . right )
self . cur = 0
self . vals = []
inorder ( root )
def next ( self ) -> int :
res = self . vals [ self . cur ]
self . cur += 1
return res
def hasNext ( self ) -> bool :
return self . cur < len ( self . vals )
# Your BSTIterator object will be instantiated and called as such:
# obj = BSTIterator(root)
# param_1 = obj.next()
# param_2 = obj.hasNext()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class BSTIterator {
private int cur = 0 ;
private List < Integer > vals = new ArrayList <> ();
public BSTIterator ( TreeNode root ) {
inorder ( root );
}
public int next () {
return vals . get ( cur ++ );
}
public boolean hasNext () {
return cur < vals . size ();
}
private void inorder ( TreeNode root ) {
if ( root != null ) {
inorder ( root . left );
vals . add ( root . val );
inorder ( root . right );
}
}
}
/**
* Your BSTIterator object will be instantiated and called as such:
* BSTIterator obj = new BSTIterator(root);
* int param_1 = obj.next();
* boolean param_2 = obj.hasNext();
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class BSTIterator {
public :
vector < int > vals ;
int cur ;
BSTIterator ( TreeNode * root ) {
cur = 0 ;
inorder ( root );
}
int next () {
return vals [ cur ++ ];
}
bool hasNext () {
return cur < vals . size ();
}
void inorder ( TreeNode * root ) {
if ( root ) {
inorder ( root -> left );
vals . push_back ( root -> val );
inorder ( root -> right );
}
}
};
/**
* Your BSTIterator object will be instantiated and called as such:
* BSTIterator* obj = new BSTIterator(root);
* int param_1 = obj->next();
* bool param_2 = obj->hasNext();
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 /**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
type BSTIterator struct {
stack [] * TreeNode
}
func Constructor ( root * TreeNode ) BSTIterator {
var stack [] * TreeNode
for ; root != nil ; root = root . Left {
stack = append ( stack , root )
}
return BSTIterator {
stack : stack ,
}
}
func ( this * BSTIterator ) Next () int {
cur := this . stack [ len ( this . stack ) - 1 ]
this . stack = this . stack [: len ( this . stack ) - 1 ]
for node := cur . Right ; node != nil ; node = node . Left {
this . stack = append ( this . stack , node )
}
return cur . Val
}
func ( this * BSTIterator ) HasNext () bool {
return len ( this . stack ) > 0
}
/**
* Your BSTIterator object will be instantiated and called as such:
* obj := Constructor(root);
* param_1 := obj.Next();
* param_2 := obj.HasNext();
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48 /**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
class BSTIterator {
private data : number [];
private index : number ;
constructor ( root : TreeNode | null ) {
this . index = 0 ;
this . data = [];
const dfs = ( root : TreeNode | null ) => {
if ( root == null ) {
return ;
}
const { val , left , right } = root ;
dfs ( left );
this . data . push ( val );
dfs ( right );
};
dfs ( root );
}
next () : number {
return this . data [ this . index ++ ];
}
hasNext () : boolean {
return this . index < this . data . length ;
}
}
/**
* Your BSTIterator object will be instantiated and called as such:
* var obj = new BSTIterator(root)
* var param_1 = obj.next()
* var param_2 = obj.hasNext()
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54 // Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
struct BSTIterator {
vals : Vec < i32 > ,
index : usize ,
}
use std :: cell :: RefCell ;
use std :: rc :: Rc ;
/**
* `&self` means the method takes an immutable reference.
* If you need a mutable reference, change it to `&mut self` instead.
*/
impl BSTIterator {
fn inorder ( root : & Option < Rc < RefCell < TreeNode >>> , res : & mut Vec < i32 > ) {
if let Some ( node ) = root {
let node = node . as_ref (). borrow ();
Self :: inorder ( & node . left , res );
res . push ( node . val );
Self :: inorder ( & node . right , res );
}
}
fn new ( root : Option < Rc < RefCell < TreeNode >>> ) -> Self {
let mut vals = vec! [];
Self :: inorder ( & root , & mut vals );
BSTIterator { vals , index : 0 }
}
fn next ( & mut self ) -> i32 {
self . index += 1 ;
self . vals [ self . index - 1 ]
}
fn has_next ( & self ) -> bool {
self . index != self . vals . len ()
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 /**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
*/
var BSTIterator = function ( root ) {
this . stack = [];
for (; root != null ; root = root . left ) {
this . stack . push ( root );
}
};
/**
* @return {number}
*/
BSTIterator . prototype . next = function () {
let cur = this . stack . pop ();
let node = cur . right ;
for (; node != null ; node = node . left ) {
this . stack . push ( node );
}
return cur . val ;
};
/**
* @return {boolean}
*/
BSTIterator . prototype . hasNext = function () {
return this . stack . length > 0 ;
};
/**
* Your BSTIterator object will be instantiated and called as such:
* var obj = new BSTIterator(root)
* var param_1 = obj.next()
* var param_2 = obj.hasNext()
*/
方法二:栈迭代
初始化时,从根节点一路遍历所有左子节点,压入栈 stack 中。
调用 next()时,弹出栈顶元素 cur,获取 cur 的右子节点 node,若 node 不为空,一直循环压入左节点。最后返回 cur.val 即可。调用 hasNext() 时,判断 stack 是否为空,空则表示迭代结束。
Python3 Java C++ TypeScript Rust
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class BSTIterator :
def __init__ ( self , root : TreeNode ):
self . stack = []
while root :
self . stack . append ( root )
root = root . left
def next ( self ) -> int :
cur = self . stack . pop ()
node = cur . right
while node :
self . stack . append ( node )
node = node . left
return cur . val
def hasNext ( self ) -> bool :
return len ( self . stack ) > 0
# Your BSTIterator object will be instantiated and called as such:
# obj = BSTIterator(root)
# param_1 = obj.next()
# param_2 = obj.hasNext()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 /**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class BSTIterator {
private Deque < TreeNode > stack = new LinkedList <> ();
public BSTIterator ( TreeNode root ) {
for (; root != null ; root = root . left ) {
stack . offerLast ( root );
}
}
public int next () {
TreeNode cur = stack . pollLast ();
for ( TreeNode node = cur . right ; node != null ; node = node . left ) {
stack . offerLast ( node );
}
return cur . val ;
}
public boolean hasNext () {
return ! stack . isEmpty ();
}
}
/**
* Your BSTIterator object will be instantiated and called as such:
* BSTIterator obj = new BSTIterator(root);
* int param_1 = obj.next();
* boolean param_2 = obj.hasNext();
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class BSTIterator {
public :
stack < TreeNode *> stack ;
BSTIterator ( TreeNode * root ) {
for (; root != nullptr ; root = root -> left ) {
stack . push ( root );
}
}
int next () {
TreeNode * cur = stack . top ();
stack . pop ();
TreeNode * node = cur -> right ;
for (; node != nullptr ; node = node -> left ) {
stack . push ( node );
}
return cur -> val ;
}
bool hasNext () {
return ! stack . empty ();
}
};
/**
* Your BSTIterator object will be instantiated and called as such:
* BSTIterator* obj = new BSTIterator(root);
* int param_1 = obj->next();
* bool param_2 = obj->hasNext();
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52 /**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
class BSTIterator {
private stack : TreeNode [];
constructor ( root : TreeNode | null ) {
this . stack = [];
const dfs = ( root : TreeNode | null ) => {
if ( root == null ) {
return ;
}
this . stack . push ( root );
dfs ( root . left );
};
dfs ( root );
}
next () : number {
const { val , right } = this . stack . pop ();
if ( right ) {
let cur = right ;
while ( cur != null ) {
this . stack . push ( cur );
cur = cur . left ;
}
}
return val ;
}
hasNext () : boolean {
return this . stack . length !== 0 ;
}
}
/**
* Your BSTIterator object will be instantiated and called as such:
* var obj = new BSTIterator(root)
* var param_1 = obj.next()
* var param_2 = obj.hasNext()
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59 // Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
struct BSTIterator {
stack : Vec < Option < Rc < RefCell < TreeNode >>>> ,
}
use std :: cell :: RefCell ;
use std :: rc :: Rc ;
/**
* `&self` means the method takes an immutable reference.
* If you need a mutable reference, change it to `&mut self` instead.
*/
impl BSTIterator {
fn dfs (
mut root : Option < Rc < RefCell < TreeNode >>> ,
stack : & mut Vec < Option < Rc < RefCell < TreeNode >>>> ,
) {
if root . is_some () {
let left = root . as_mut (). unwrap (). borrow_mut (). left . take ();
stack . push ( root );
Self :: dfs ( left , stack );
}
}
fn new ( root : Option < Rc < RefCell < TreeNode >>> ) -> Self {
let mut stack = vec! [];
Self :: dfs ( root , & mut stack );
BSTIterator { stack }
}
fn next ( & mut self ) -> i32 {
let node = self . stack . pop (). unwrap (). unwrap ();
let mut node = node . borrow_mut ();
if node . right . is_some () {
Self :: dfs ( node . right . take (), & mut self . stack );
}
node . val
}
fn has_next ( & self ) -> bool {
self . stack . len () != 0
}
}