


题目描述
给你一个二进制矩阵 matrix ,它的大小为 m x n ,你可以将 matrix 中的 列 按任意顺序重新排列。
请你返回最优方案下将 matrix 重新排列后,全是 1 的子矩阵面积。
示例 1:
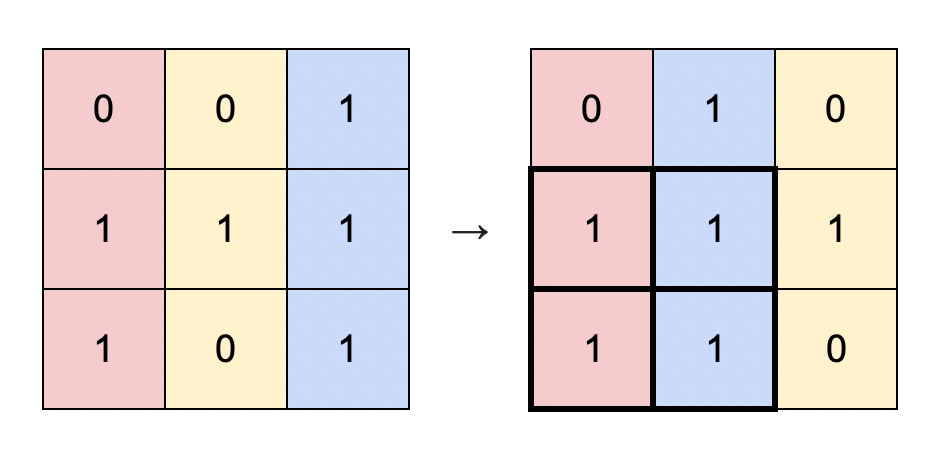
输入:matrix = [[0,0,1],[1,1,1],[1,0,1]]
输出:4
解释:你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分,面积为 4 。
示例 2:

输入:matrix = [[1,0,1,0,1]]
输出:3
解释:你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分,面积为 3 。
示例 3:
输入:matrix = [[1,1,0],[1,0,1]]
输出:2
解释:由于你只能整列整列重新排布,所以没有比面积为 2 更大的全 1 子矩形。
示例 4:
输入:matrix = [[0,0],[0,0]]
输出:0
解释:由于矩阵中没有 1 ,没有任何全 1 的子矩阵,所以面积为 0 。
提示:
m == matrix.lengthn == matrix[i].length1 <= m * n <= 105matrix[i][j] 要么是 0 ,要么是 1 。
解法
方法一:预处理 + 排序
由于题目中矩阵是按列进行重排,因此,我们可以先对矩阵的每一列进行预处理。
对于每个值为 \(1\) 的元素,我们更新其值为该元素向上的最大连续的 \(1\) 的个数,即 \(matrix[i][j]=matrix[i-1][j]+1\)。
接下来,我们可以对更新后的矩阵的每一行进行排序。然后遍历每一行,计算以该行作为底边的最大全 \(1\) 子矩阵的面积。具体计算逻辑如下:
对于矩阵的某一行,我们记第 \(k\) 大元素的值为 \(val_k\),其中 \(k \geq 1\),那么该行至少有 \(k\) 个元素不小于 \(val_k\),组成的全 \(1\) 子矩阵面积为 \(val_k \times k\)。从大到小遍历矩阵该行的每个元素,取 \(val_k \times k\) 的最大值,更新答案。
时间复杂度 \(O(m \times n \times \log n)\)。其中 \(m\) 和 \(n\) 分别为矩阵的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12 | class Solution:
def largestSubmatrix(self, matrix: List[List[int]]) -> int:
for i in range(1, len(matrix)):
for j in range(len(matrix[0])):
if matrix[i][j]:
matrix[i][j] = matrix[i - 1][j] + 1
ans = 0
for row in matrix:
row.sort(reverse=True)
for j, v in enumerate(row, 1):
ans = max(ans, j * v)
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | class Solution {
public int largestSubmatrix(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
for (int i = 1; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (matrix[i][j] == 1) {
matrix[i][j] = matrix[i - 1][j] + 1;
}
}
}
int ans = 0;
for (var row : matrix) {
Arrays.sort(row);
for (int j = n - 1, k = 1; j >= 0 && row[j] > 0; --j, ++k) {
int s = row[j] * k;
ans = Math.max(ans, s);
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | class Solution {
public:
int largestSubmatrix(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
for (int i = 1; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (matrix[i][j]) {
matrix[i][j] = matrix[i - 1][j] + 1;
}
}
}
int ans = 0;
for (auto& row : matrix) {
sort(row.rbegin(), row.rend());
for (int j = 0; j < n; ++j) {
ans = max(ans, (j + 1) * row[j]);
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | func largestSubmatrix(matrix [][]int) int {
m, n := len(matrix), len(matrix[0])
for i := 1; i < m; i++ {
for j := 0; j < n; j++ {
if matrix[i][j] == 1 {
matrix[i][j] = matrix[i-1][j] + 1
}
}
}
ans := 0
for _, row := range matrix {
sort.Ints(row)
for j, k := n-1, 1; j >= 0 && row[j] > 0; j, k = j-1, k+1 {
ans = max(ans, row[j]*k)
}
}
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 | function largestSubmatrix(matrix: number[][]): number {
for (let column = 0; column < matrix[0].length; column++) {
for (let row = 0; row < matrix.length; row++) {
let tempRow = row;
let count = 0;
while (tempRow < matrix.length && matrix[tempRow][column] === 1) {
count++;
tempRow++;
}
while (count !== 0) {
matrix[row][column] = count;
count--;
row++;
}
}
}
for (let row = 0; row < matrix.length; row++) {
matrix[row].sort((a, b) => a - b);
}
let maxSubmatrixArea = 0;
for (let row = 0; row < matrix.length; row++) {
for (let col = matrix[row].length - 1; col >= 0; col--) {
maxSubmatrixArea = Math.max(
maxSubmatrixArea,
matrix[row][col] * (matrix[row].length - col),
);
}
}
return maxSubmatrixArea;
}
|




