跳转至

1692. 计算分配糖果的不同方式 🔒

题目描述

现有 n 颗 不同 糖果（分别标记为 1 到 n ）和 k 个相同的手袋。请把糖果分配到各个手袋中并保证每个手袋里至少有一颗糖果。

不考虑手袋和糖果的摆放顺序，会有多种不同的分配方式。如果某种分配方式中其中一个手袋里的糖果与另一种分配方式中所有手袋里的糖果都不相同，则认为这两种分配方式不同。

例如，(1), (2,3) 与(2), (1,3)的分配方式是不同的，因为第一种分配方式中手袋(2,3)里的糖果2和3，在第二种分配方式中被分配到了手袋(2)和(1,3) 中。

已知整数 n 和 k, 请返回分配糖果的不同方式。返回的答案如果数值太大，请取109 + 7的模，并返回。

 

示例 1：

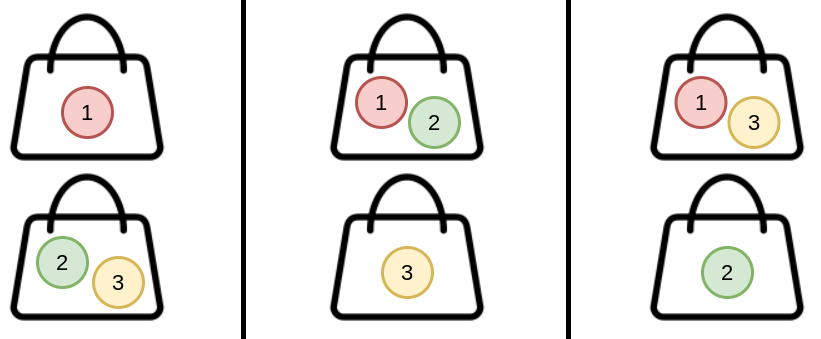
输入：n = 3, k = 2
输出：3
解释：把糖果 3 分配到 2 个手袋中的一个，共有 3 种方式:
(1), (2,3)
(1,2), (3)
(1,3), (2)

示例 2：

输入：n = 4, k = 2
输出：7
解释：把糖果 4 分配到 2 个手袋中的一个，共有 7 种方式:
(1), (2,3,4)
(1,2), (3,4)
(1,3), (2,4)
(1,4), (2,3)
(1,2,3), (4)
(1,2,4), (3)
(1,3,4), (2)

示例 3：

输入：n = 20, k = 5
输出：206085257
解释：把 20 颗糖果分配到 5 个手袋种，共有 1881780996 种方式。1881780996 取 109 + 7的模，等于 206085257。

 

提示：

  • 1 <= k <= n <= 1000

解法

方法一：动态规划

我们定义 $f[i][j]$ 表示将 $i$ 个糖果分配给 $j$ 个手袋的不同分配方式的数量。初始时 $f[0][0]=1$，答案为 $f[n][k]$。

我们考虑第 $i$ 个糖果如何分配，如果第 $i$ 个糖果分配给一个新的手袋，那么 $f[i][j]=f[i-1][j-1]$；如果第 $i$ 个糖果分配给一个已有的手袋，那么 $f[i][j]=f[i-1][j]\times j$。因此，状态转移方程为：

$$ f[i][j]=f[i-1][j-1]+f[i-1][j]\times j $$

最终的答案为 $f[n][k]$。

时间复杂度 $O(n \times k)$，空间复杂度 $O(n \times k)$。其中 $n$ 和 $k$ 分别为糖果的数量和手袋的数量。

1
2
3
4
5
6
7
8
9
class Solution:
    def waysToDistribute(self, n: int, k: int) -> int:
        mod = 10**9 + 7
        f = [[0] * (k + 1) for _ in range(n + 1)]
        f[0][0] = 1
        for i in range(1, n + 1):
            for j in range(1, k + 1):
                f[i][j] = (f[i - 1][j] * j + f[i - 1][j - 1]) % mod
        return f[n][k]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution {
    public int waysToDistribute(int n, int k) {
        final int mod = (int) 1e9 + 7;
        int[][] f = new int[n + 1][k + 1];
        f[0][0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= k; j++) {
                f[i][j] = (int) ((long) f[i - 1][j] * j % mod + f[i - 1][j - 1]) % mod;
            }
        }
        return f[n][k];
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution {
public:
    int waysToDistribute(int n, int k) {
        const int mod = 1e9 + 7;
        int f[n + 1][k + 1];
        memset(f, 0, sizeof(f));
        f[0][0] = 1;
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= k; ++j) {
                f[i][j] = (1LL * f[i - 1][j] * j + f[i - 1][j - 1]) % mod;
            }
        }
        return f[n][k];
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
func waysToDistribute(n int, k int) int {
    f := make([][]int, n+1)
    for i := range f {
        f[i] = make([]int, k+1)
    }
    f[0][0] = 1
    const mod = 1e9 + 7
    for i := 1; i <= n; i++ {
        for j := 1; j <= k; j++ {
            f[i][j] = (f[i-1][j]*j + f[i-1][j-1]) % mod
        }
    }
    return f[n][k]
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
function waysToDistribute(n: number, k: number): number {
    const mod = 10 ** 9 + 7;
    const f: number[][] = Array.from({ length: n + 1 }, () =>
        Array.from({ length: k + 1 }, () => 0),
    );
    f[0][0] = 1;
    for (let i = 1; i <= n; ++i) {
        for (let j = 1; j <= k; ++j) {
            f[i][j] = (f[i - 1][j] * j + f[i - 1][j - 1]) % mod;
        }
    }
    return f[n][k];
}

评论