跳转至

1676. 二叉树的最近公共祖先 IV 🔒

题目描述

给定一棵二叉树的根节点 root 和 TreeNode 类对象的数组（列表） nodes，返回 nodes 中所有节点的最近公共祖先（LCA）。数组（列表）中所有节点都存在于该二叉树中，且二叉树中所有节点的值都是互不相同的。

我们扩展二叉树的最近公共祖先节点在维基百科上的定义：“对于任意合理的 i 值， n 个节点 p1 、 p2、...、 pn 在二叉树 T 中的最近公共祖先节点是后代中包含所有节点 pi 的最深节点（我们允许一个节点是其自身的后代）”。一个节点 x 的后代节点是节点 x 到某一叶节点间的路径中的节点 y。

 

示例 1:

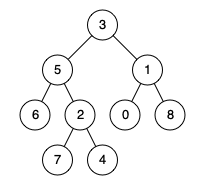
输入: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [4,7]
输出: 2
解释: 节点 4 和 7 的最近公共祖先是 2。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [1]
输出: 1
解释: 单个节点的最近公共祖先是该节点本身。

示例 3:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [7,6,2,4]
输出: 5
解释: 节点 7、6、2 和 4 的最近公共祖先节点是 5。

示例 4:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [0,1,2,3,4,5,6,7,8]
输出: 3
解释: 树中所有节点的最近公共祖先是根节点。

 

提示:

  • 树中节点个数的范围是 [1, 104] 。
  • -109 <= Node.val <= 109
  • 所有的 Node.val 都是互不相同的。
  • 所有的 nodes[i] 都存在于该树中。
  • 所有的 nodes[i] 都是互不相同的。

解法

方法一：哈希表 + DFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None


class Solution:
    def lowestCommonAncestor(
        self, root: 'TreeNode', nodes: 'List[TreeNode]'
    ) -> 'TreeNode':
        def dfs(root):
            if root is None or root.val in s:
                return root
            left, right = dfs(root.left), dfs(root.right)
            if left and right:
                return root
            return left or right

        s = {node.val for node in nodes}
        return dfs(root)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private Set<Integer> s = new HashSet<>();

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode[] nodes) {
        for (TreeNode node : nodes) {
            s.add(node.val);
        }
        return dfs(root);
    }

    private TreeNode dfs(TreeNode root) {
        if (root == null || s.contains(root.val)) {
            return root;
        }
        TreeNode left = dfs(root.left);
        TreeNode right = dfs(root.right);
        if (left == null) {
            return right;
        }
        if (right == null) {
            return left;
        }
        return root;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, vector<TreeNode*>& nodes) {
        unordered_set<int> s;
        for (auto node : nodes) s.insert(node->val);
        function<TreeNode*(TreeNode*)> dfs = [&](TreeNode* root) -> TreeNode* {
            if (!root || s.count(root->val)) return root;
            auto left = dfs(root->left);
            auto right = dfs(root->right);
            if (!left) return right;
            if (!right) return left;
            return root;
        };
        return dfs(root);
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode[]} nodes
 * @return {TreeNode}
 */
var lowestCommonAncestor = function (root, nodes) {
    const s = new Set();
    for (const node of nodes) {
        s.add(node.val);
    }
    function dfs(root) {
        if (!root || s.has(root.val)) {
            return root;
        }
        const [left, right] = [dfs(root.left), dfs(root.right)];
        if (left && right) {
            return root;
        }
        return left || right;
    }
    return dfs(root);
};

评论