跳转至

1666. 改变二叉树的根节点 🔒

题目描述

给定一棵二叉树的根节点 root 和一个叶节点 leaf ，更改二叉树，使得 leaf 为新的根节点。

你可以按照下列步骤修改从 leaf 到 root 的路径中除 root 外的每个节点 cur ：

  1. 如果 cur 有左子节点，则该子节点变为 cur 的右子节点。注意我们保证 cur 至多有一个子节点。
  2. cur 的原父节点变为 cur 的左子节点。

返回修改后新树的根节点。

注意：确保你的答案在操作后正确地设定了 Node.parent （父节点）指针，否则会被判为错误答案。

 

示例 1:

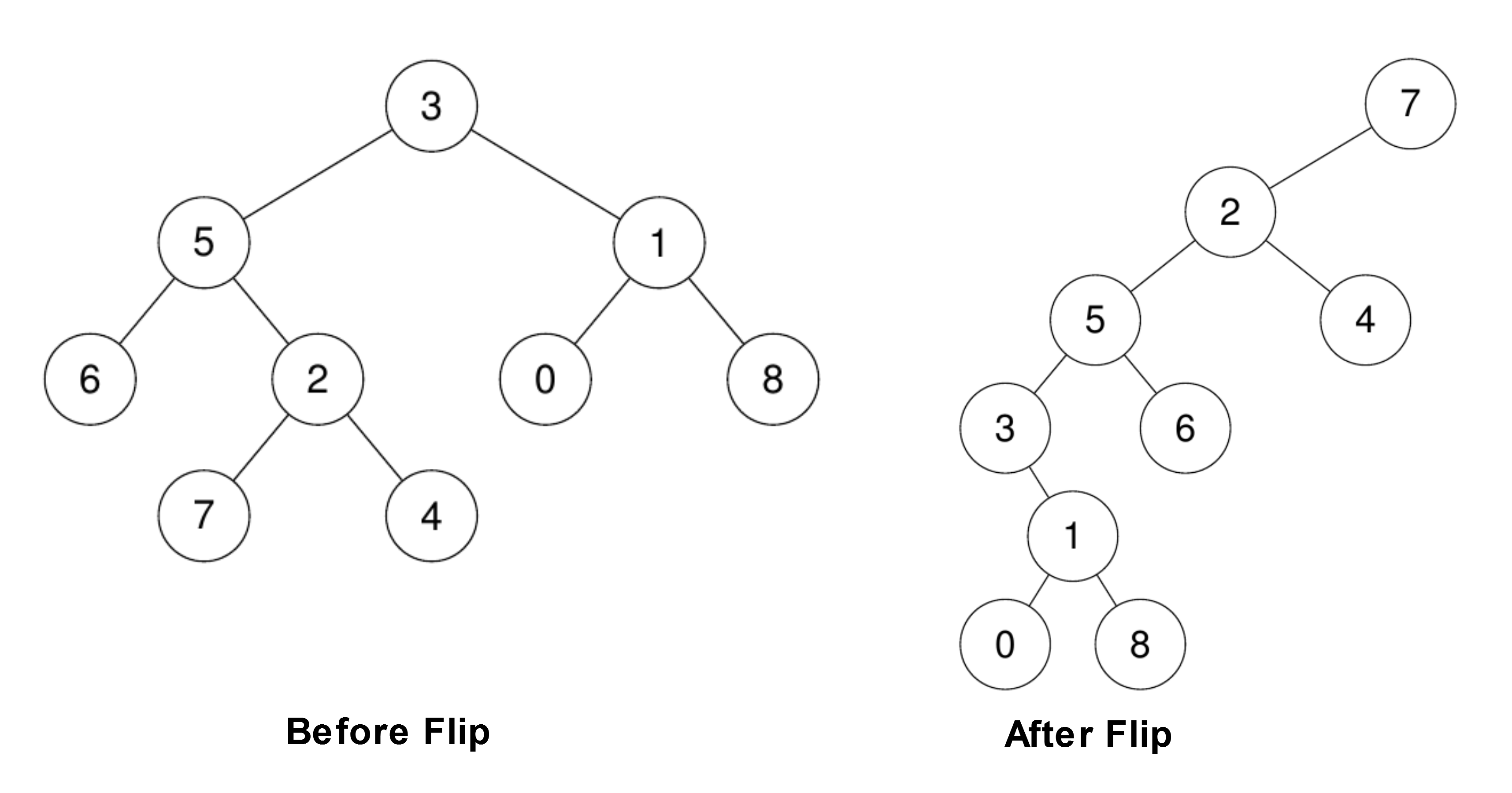
输入: root = [3,5,1,6,2,0,8,null,null,7,4], leaf = 7
输出: [7,2,null,5,4,3,6,null,null,null,1,null,null,0,8]

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], leaf = 0
输出: [0,1,null,3,8,5,null,null,null,6,2,null,null,7,4]

 

提示:

  • 树中节点的个数在范围 [2, 100] 内。
  • -109 <= Node.val <= 109
  • 所有的 Node.val 都是唯一的。
  • leaf 存在于树中。

解法

方法一：自底向上模拟

从叶节点 leaf 开始，向上模拟翻转操作。

时间复杂度 $O(n)$，空间复杂度 $O(1)$。其中 $n$ 为二叉树节点个数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
"""
# Definition for a Node.
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        self.parent = None
"""


class Solution:
    def flipBinaryTree(self, root: "Node", leaf: "Node") -> "Node":
        cur = leaf
        p = cur.parent
        while cur != root:
            gp = p.parent
            if cur.left:
                cur.right = cur.left
            cur.left = p
            p.parent = cur
            if p.left == cur:
                p.left = None
            elif p.right == cur:
                p.right = None
            cur = p
            p = gp
        leaf.parent = None
        return leaf

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
};
*/

class Solution {
    public Node flipBinaryTree(Node root, Node leaf) {
        Node cur = leaf;
        Node p = cur.parent;
        while (cur != root) {
            Node gp = p.parent;
            if (cur.left != null) {
                cur.right = cur.left;
            }
            cur.left = p;
            p.parent = cur;
            if (p.left == cur) {
                p.left = null;
            } else if (p.right == cur) {
                p.right = null;
            }
            cur = p;
            p = gp;
        }
        leaf.parent = null;
        return leaf;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/*
// Definition for a Node->
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* parent;
};
*/

class Solution {
public:
    Node* flipBinaryTree(Node* root, Node* leaf) {
        Node* cur = leaf;
        Node* p = cur->parent;
        while (cur != root) {
            Node* gp = p->parent;
            if (cur->left) {
                cur->right = cur->left;
            }
            cur->left = p;
            p->parent = cur;
            if (p->left == cur) {
                p->left = nullptr;
            } else if (p->right == cur) {
                p->right = nullptr;
            }
            cur = p;
            p = gp;
        }
        leaf->parent = nullptr;
        return leaf;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * // Definition for a Node.
 * function Node(val) {
 *    this.val = val;
 *    this.left = null;
 *    this.right = null;
 *    this.parent = null;
 * };
 */

/**
 * @param {Node} node
 * @return {Node}
 */
var flipBinaryTree = function (root, leaf) {
    let cur = leaf;
    let p = cur.parent;
    while (cur != root) {
        const gp = p.parent;
        if (cur.left != null) {
            cur.right = cur.left;
        }
        cur.left = p;
        p.parent = cur;
        if (p.left == cur) {
            p.left = null;
        } else if (p.right == cur) {
            p.right = null;
        }
        cur = p;
        p = gp;
    }
    leaf.parent = null;
    return leaf;
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/*
// Definition for a Node.
public class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
}
*/

public class Solution {
    public Node FlipBinaryTree(Node root, Node leaf) {
        Node cur = leaf;
        Node p = cur.parent;
        while (cur != root) {
            Node gp = p.parent;
            if (cur.left != null) {
                cur.right = cur.left;
            }
            cur.left = p;
            p.parent = cur;
            if (p.left == cur) {
                p.left = null;
            } else if (p.right == cur) {
                p.right = null;
            }
            cur = p;
            p = gp;
        }
        leaf.parent = null;
        return leaf;
    }
}

评论