


题目描述
给你 n 个二维平面上的点 points ,其中 points[i] = [xi, yi] ,请你返回两点之间内部不包含任何点的 最宽垂直区域 的宽度。
垂直区域 的定义是固定宽度,而 y 轴上无限延伸的一块区域(也就是高度为无穷大)。 最宽垂直区域 为宽度最大的一个垂直区域。
请注意,垂直区域 边上 的点 不在 区域内。
示例 1:
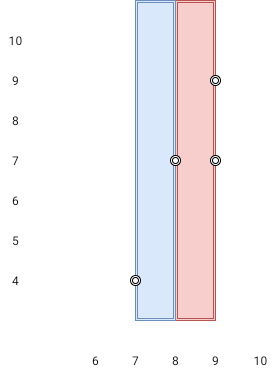
输入:points = [[8,7],[9,9],[7,4],[9,7]]
输出:1
解释:红色区域和蓝色区域都是最优区域。
示例 2:
输入:points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]
输出:3
提示:
n == points.length2 <= n <= 105points[i].length == 20 <= xi, yi <= 109
解法
方法一:排序
我们可以对数组 \(points\) 按照 \(x\) 升序排列,获取相邻点之间 \(x\) 的差值的最大值。
时间复杂度 \(O(n \times \log n)\),空间复杂度 \(O(\log n)\)。其中 \(n\) 为数组 \(points\) 的长度。
| class Solution:
def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:
points.sort()
return max(b[0] - a[0] for a, b in pairwise(points))
|
| class Solution {
public int maxWidthOfVerticalArea(int[][] points) {
Arrays.sort(points, (a, b) -> a[0] - b[0]);
int ans = 0;
for (int i = 0; i < points.length - 1; ++i) {
ans = Math.max(ans, points[i + 1][0] - points[i][0]);
}
return ans;
}
}
|
| class Solution {
public:
int maxWidthOfVerticalArea(vector<vector<int>>& points) {
sort(points.begin(), points.end());
int ans = 0;
for (int i = 0; i < points.size() - 1; ++i) {
ans = max(ans, points[i + 1][0] - points[i][0]);
}
return ans;
}
};
|
| func maxWidthOfVerticalArea(points [][]int) (ans int) {
sort.Slice(points, func(i, j int) bool { return points[i][0] < points[j][0] })
for i, p := range points[1:] {
ans = max(ans, p[0]-points[i][0])
}
return
}
|
| function maxWidthOfVerticalArea(points: number[][]): number {
points.sort((a, b) => a[0] - b[0]);
let ans = 0;
for (let i = 1; i < points.length; ++i) {
ans = Math.max(ans, points[i][0] - points[i - 1][0]);
}
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | /**
* @param {number[][]} points
* @return {number}
*/
var maxWidthOfVerticalArea = function (points) {
points.sort((a, b) => a[0] - b[0]);
let ans = 0;
let px = points[0][0];
for (const [x, _] of points) {
ans = Math.max(ans, x - px);
px = x;
}
return ans;
};
|
方法二:桶排序
方法一中排序的时间复杂度为 \(O(n \times \log n)\),其实我们可以利用桶排序的思想,将时间复杂度降低到 \(O(n)\)。
我们将数组 \(points\) 的横坐标放入数组 \(nums\) 中。
假设数组 \(nums\) 有 \(n\) 个元素,所有元素从小到大依次是 \(nums_0\) 到 \(nums_{n - 1}\),最大间距是 \(maxGap\)。考虑数组中的最大元素和最小元素之差:
\[
nums_{n - 1} - nums_0 = \sum_{i = 1}^{n - 1} (nums_i - nums_{i - 1}) \le{maxGap} \times (n - 1)
\]
因此 \(maxGap \ge \dfrac{nums_{n - 1} - nums_0}{n - 1}\),即最大间距至少为 \(\dfrac{nums_{n - 1} - nums_0}{n - 1}\)。
可以利用桶排序的思想,设定桶的大小(即每个桶最多包含的不同元素个数)为 \(\dfrac{nums_{n - 1} - nums_0}{n - 1}\),将元素按照元素值均匀分布到各个桶内,则同一个桶内的任意两个元素之差小于 \({maxGap}\),差为 \({maxGap}\) 的两个元素一定在两个不同的桶内。对于每个桶,维护桶内的最小值和最大值,初始时每个桶内的最小值和最大值分别是正无穷和负无穷,表示桶内没有元素。
遍历数组 \({nums}\) 中的所有元素。对于每个元素,根据该元素与最小元素之差以及桶的大小计算该元素应该分到的桶的编号,可以确保编号小的桶内的元素都小于编号大的桶内的元素,使用元素值更新元素所在的桶内的最小值和最大值。
遍历数组结束之后,每个非空的桶内的最小值和最大值都可以确定。按照桶的编号从小到大的顺序依次遍历每个桶,当前的桶的最小值和上一个非空的桶的最大值是排序后的相邻元素,计算两个相邻元素之差,并更新最大间距。遍历桶结束之后即可得到最大间距。
时间复杂度 \(O(n)\),空间复杂度 \(O(n)\)。其中 \(n\) 为数组 \(points\) 的长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | class Solution:
def maxWidthOfVerticalArea(self, points: List[List[int]]) -> int:
nums = [x for x, _ in points]
n = len(nums)
mi, mx = min(nums), max(nums)
bucket_size = max(1, (mx - mi) // (n - 1))
bucket_count = (mx - mi) // bucket_size + 1
buckets = [[inf, -inf] for _ in range(bucket_count)]
for x in nums:
i = (x - mi) // bucket_size
buckets[i][0] = min(buckets[i][0], x)
buckets[i][1] = max(buckets[i][1], x)
ans = 0
prev = inf
for curmin, curmax in buckets:
if curmin > curmax:
continue
ans = max(ans, curmin - prev)
prev = curmax
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 | class Solution {
public int maxWidthOfVerticalArea(int[][] points) {
int n = points.length;
int[] nums = new int[n];
for (int i = 0; i < n; ++i) {
nums[i] = points[i][0];
}
final int inf = 1 << 30;
int mi = inf, mx = -inf;
for (int v : nums) {
mi = Math.min(mi, v);
mx = Math.max(mx, v);
}
int bucketSize = Math.max(1, (mx - mi) / (n - 1));
int bucketCount = (mx - mi) / bucketSize + 1;
int[][] buckets = new int[bucketCount][2];
for (var bucket : buckets) {
bucket[0] = inf;
bucket[1] = -inf;
}
for (int v : nums) {
int i = (v - mi) / bucketSize;
buckets[i][0] = Math.min(buckets[i][0], v);
buckets[i][1] = Math.max(buckets[i][1], v);
}
int prev = inf;
int ans = 0;
for (var bucket : buckets) {
if (bucket[0] > bucket[1]) {
continue;
}
ans = Math.max(ans, bucket[0] - prev);
prev = bucket[1];
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 | class Solution {
public:
int maxWidthOfVerticalArea(vector<vector<int>>& points) {
int n = points.size();
vector<int> nums;
for (auto& p : points) {
nums.push_back(p[0]);
}
const int inf = 1 << 30;
int mi = inf, mx = -inf;
for (int v : nums) {
mi = min(mi, v);
mx = max(mx, v);
}
int bucketSize = max(1, (mx - mi) / (n - 1));
int bucketCount = (mx - mi) / bucketSize + 1;
vector<pair<int, int>> buckets(bucketCount, {inf, -inf});
for (int v : nums) {
int i = (v - mi) / bucketSize;
buckets[i].first = min(buckets[i].first, v);
buckets[i].second = max(buckets[i].second, v);
}
int ans = 0;
int prev = inf;
for (auto [curmin, curmax] : buckets) {
if (curmin > curmax) continue;
ans = max(ans, curmin - prev);
prev = curmax;
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | func maxWidthOfVerticalArea(points [][]int) (ans int) {
n := len(points)
nums := make([]int, 0, n)
for _, p := range points {
nums = append(nums, p[0])
}
const inf = 1 << 30
mi, mx := inf, -inf
for _, v := range nums {
mi = min(mi, v)
mx = max(mx, v)
}
bucketSize := max(1, (mx-mi)/(n-1))
bucketCount := (mx-mi)/bucketSize + 1
buckets := make([][]int, bucketCount)
for i := range buckets {
buckets[i] = []int{inf, -inf}
}
for _, v := range nums {
i := (v - mi) / bucketSize
buckets[i][0] = min(buckets[i][0], v)
buckets[i][1] = max(buckets[i][1], v)
}
prev := inf
for _, bucket := range buckets {
if bucket[0] > bucket[1] {
continue
}
ans = max(ans, bucket[0]-prev)
prev = bucket[1]
}
return ans
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | function maxWidthOfVerticalArea(points: number[][]): number {
const nums: number[] = points.map(point => point[0]);
const inf = 1 << 30;
const n = nums.length;
let mi = inf;
let mx = -inf;
for (const x of nums) {
mi = Math.min(mi, x);
mx = Math.max(mx, x);
}
const bucketSize = Math.max(1, Math.floor((mx - mi) / (n - 1)));
const bucketCount = Math.floor((mx - mi) / bucketSize) + 1;
const buckets = new Array(bucketCount).fill(0).map(() => [inf, -inf]);
for (const x of nums) {
const i = Math.floor((x - mi) / bucketSize);
buckets[i][0] = Math.min(buckets[i][0], x);
buckets[i][1] = Math.max(buckets[i][1], x);
}
let prev = inf;
let ans = 0;
for (const [left, right] of buckets) {
if (left > right) {
continue;
}
ans = Math.max(ans, left - prev);
prev = right;
}
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | /**
* @param {number[][]} points
* @return {number}
*/
var maxWidthOfVerticalArea = function (points) {
const nums = points.map(point => point[0]);
const inf = 1 << 30;
const n = nums.length;
let mi = inf;
let mx = -inf;
for (const x of nums) {
mi = Math.min(mi, x);
mx = Math.max(mx, x);
}
const bucketSize = Math.max(1, Math.floor((mx - mi) / (n - 1)));
const bucketCount = Math.floor((mx - mi) / bucketSize) + 1;
const buckets = new Array(bucketCount).fill(0).map(() => [inf, -inf]);
for (const x of nums) {
const i = Math.floor((x - mi) / bucketSize);
buckets[i][0] = Math.min(buckets[i][0], x);
buckets[i][1] = Math.max(buckets[i][1], x);
}
let prev = inf;
let ans = 0;
for (const [left, right] of buckets) {
if (left > right) {
continue;
}
ans = Math.max(ans, left - prev);
prev = right;
}
return ans;
};
|



