


题目描述
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
示例 1:
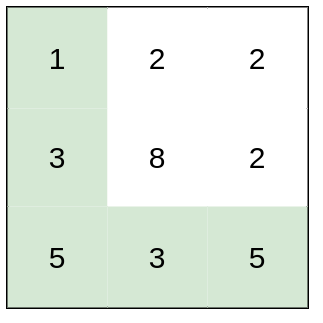
输入:heights = [[1,2,2],[3,8,2],[5,3,5]]
输出:2
解释:路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优,因为另一条路径差值最大值为 3 。
示例 2:
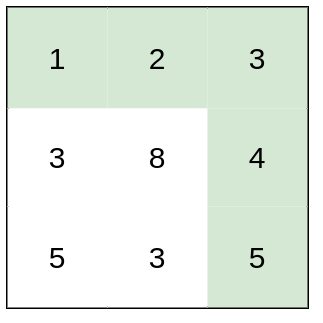
输入:heights = [[1,2,3],[3,8,4],[5,3,5]]
输出:1
解释:路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ,比路径 [1,3,5,3,5] 更优。
示例 3:
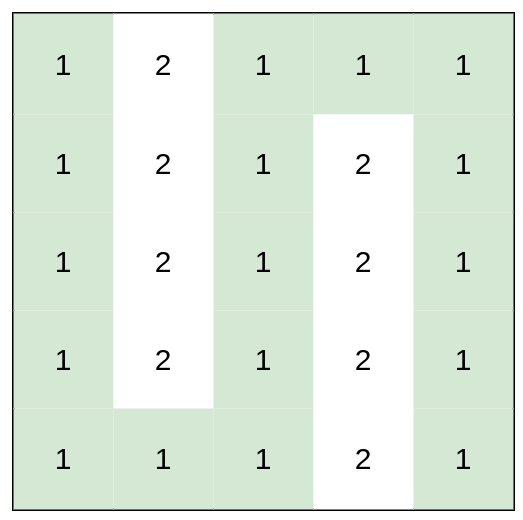
输入:heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出:0
解释:上图所示路径不需要消耗任何体力。
提示:
rows == heights.lengthcolumns == heights[i].length1 <= rows, columns <= 1001 <= heights[i][j] <= 106
解法
方法一:并查集
对于本题,我们可以把每个格子当做图的一个节点,把相邻两个格子的高度差绝对值当做边的权重,因此本题是求解从最左上角的节点到最右下角的节点的连通性问题。
我们先构建一个边集,然后按照边的权重从小到大进行排序,逐个添加边,直到最左上角的节点和最右下角的节点连通为止,此时的边的权重就是题目的最小体力消耗值。
时间复杂度 \(O(m \times n \times \log(m \times n))\),空间复杂度 \(O(m \times n)\)。其中 \(m\) 和 \(n\) 分别是二维数组的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46 | class UnionFind:
def __init__(self, n):
self.p = list(range(n))
self.size = [1] * n
def find(self, x):
if self.p[x] != x:
self.p[x] = self.find(self.p[x])
return self.p[x]
def union(self, a, b):
pa, pb = self.find(a), self.find(b)
if pa == pb:
return False
if self.size[pa] > self.size[pb]:
self.p[pb] = pa
self.size[pa] += self.size[pb]
else:
self.p[pa] = pb
self.size[pb] += self.size[pa]
return True
def connected(self, a, b):
return self.find(a) == self.find(b)
class Solution:
def minimumEffortPath(self, heights: List[List[int]]) -> int:
m, n = len(heights), len(heights[0])
uf = UnionFind(m * n)
e = []
dirs = (0, 1, 0)
for i in range(m):
for j in range(n):
for a, b in pairwise(dirs):
x, y = i + a, j + b
if 0 <= x < m and 0 <= y < n:
e.append(
(abs(heights[i][j] - heights[x][y]), i * n + j, x * n + y)
)
e.sort()
for h, a, b in e:
uf.union(a, b)
if uf.connected(0, m * n - 1):
return h
return 0
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67 | class UnionFind {
private final int[] p;
private final int[] size;
public UnionFind(int n) {
p = new int[n];
size = new int[n];
for (int i = 0; i < n; ++i) {
p[i] = i;
size[i] = 1;
}
}
public int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
public boolean union(int a, int b) {
int pa = find(a), pb = find(b);
if (pa == pb) {
return false;
}
if (size[pa] > size[pb]) {
p[pb] = pa;
size[pa] += size[pb];
} else {
p[pa] = pb;
size[pb] += size[pa];
}
return true;
}
public boolean connected(int a, int b) {
return find(a) == find(b);
}
}
class Solution {
public int minimumEffortPath(int[][] heights) {
int m = heights.length, n = heights[0].length;
UnionFind uf = new UnionFind(m * n);
List<int[]> edges = new ArrayList<>();
int[] dirs = {1, 0, 1};
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
for (int k = 0; k < 2; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x >= 0 && x < m && y >= 0 && y < n) {
int d = Math.abs(heights[i][j] - heights[x][y]);
edges.add(new int[] {d, i * n + j, x * n + y});
}
}
}
}
Collections.sort(edges, (a, b) -> a[0] - b[0]);
for (int[] e : edges) {
uf.union(e[1], e[2]);
if (uf.connected(0, m * n - 1)) {
return e[0];
}
}
return 0;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65 | class UnionFind {
public:
UnionFind(int n) {
p = vector<int>(n);
size = vector<int>(n, 1);
iota(p.begin(), p.end(), 0);
}
bool unite(int a, int b) {
int pa = find(a), pb = find(b);
if (pa == pb) {
return false;
}
if (size[pa] > size[pb]) {
p[pb] = pa;
size[pa] += size[pb];
} else {
p[pa] = pb;
size[pb] += size[pa];
}
return true;
}
int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
bool connected(int a, int b) {
return find(a) == find(b);
}
private:
vector<int> p, size;
};
class Solution {
public:
int minimumEffortPath(vector<vector<int>>& heights) {
int m = heights.size(), n = heights[0].size();
vector<array<int, 3>> edges;
int dirs[3] = {0, 1, 0};
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
for (int k = 0; k < 2; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x >= 0 && x < m && y >= 0 && y < n) {
edges.push_back({abs(heights[i][j] - heights[x][y]), i * n + j, x * n + y});
}
}
}
}
sort(edges.begin(), edges.end());
UnionFind uf(m * n);
for (auto& [h, a, b] : edges) {
uf.unite(a, b);
if (uf.connected(0, m * n - 1)) {
return h;
}
}
return 0;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71 | type unionFind struct {
p, size []int
}
func newUnionFind(n int) *unionFind {
p := make([]int, n)
size := make([]int, n)
for i := range p {
p[i] = i
size[i] = 1
}
return &unionFind{p, size}
}
func (uf *unionFind) find(x int) int {
if uf.p[x] != x {
uf.p[x] = uf.find(uf.p[x])
}
return uf.p[x]
}
func (uf *unionFind) union(a, b int) bool {
pa, pb := uf.find(a), uf.find(b)
if pa == pb {
return false
}
if uf.size[pa] > uf.size[pb] {
uf.p[pb] = pa
uf.size[pa] += uf.size[pb]
} else {
uf.p[pa] = pb
uf.size[pb] += uf.size[pa]
}
return true
}
func (uf *unionFind) connected(a, b int) bool {
return uf.find(a) == uf.find(b)
}
func minimumEffortPath(heights [][]int) int {
m, n := len(heights), len(heights[0])
edges := make([][3]int, 0, m*n*2)
dirs := [3]int{0, 1, 0}
for i, row := range heights {
for j, h := range row {
for k := 0; k < 2; k++ {
x, y := i+dirs[k], j+dirs[k+1]
if x >= 0 && x < m && y >= 0 && y < n {
edges = append(edges, [3]int{abs(h - heights[x][y]), i*n + j, x*n + y})
}
}
}
}
sort.Slice(edges, func(i, j int) bool { return edges[i][0] < edges[j][0] })
uf := newUnionFind(m * n)
for _, e := range edges {
uf.union(e[1], e[2])
if uf.connected(0, m*n-1) {
return e[0]
}
}
return 0
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68 | class UnionFind {
private p: number[];
private size: number[];
constructor(n: number) {
this.p = Array.from({ length: n }, (_, i) => i);
this.size = Array(n).fill(1);
}
find(x: number): number {
if (this.p[x] !== x) {
this.p[x] = this.find(this.p[x]);
}
return this.p[x];
}
union(a: number, b: number): boolean {
const pa = this.find(a);
const pb = this.find(b);
if (pa === pb) {
return false;
}
if (this.size[pa] > this.size[pb]) {
this.p[pb] = pa;
this.size[pa] += this.size[pb];
} else {
this.p[pa] = pb;
this.size[pb] += this.size[pa];
}
return true;
}
connected(a: number, b: number): boolean {
return this.find(a) === this.find(b);
}
}
function minimumEffortPath(heights: number[][]): number {
const m = heights.length;
const n = heights[0].length;
const uf = new UnionFind(m * n);
const edges: number[][] = [];
const dirs = [1, 0, 1];
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
for (let k = 0; k < 2; ++k) {
const x = i + dirs[k];
const y = j + dirs[k + 1];
if (x >= 0 && x < m && y >= 0 && y < n) {
const d = Math.abs(heights[i][j] - heights[x][y]);
edges.push([d, i * n + j, x * n + y]);
}
}
}
}
edges.sort((a, b) => a[0] - b[0]);
for (const [h, a, b] of edges) {
uf.union(a, b);
if (uf.connected(0, m * n - 1)) {
return h;
}
}
return 0;
}
|
方法二:二分查找 + BFS
我们注意到,如果一个路径的最大体力消耗值为 \(x\),那么对于任意 \(y > x\),该路径也是满足条件的,这存在着单调性,因此我们可以使用二分查找的方法,找到最小的满足条件的体力消耗值。
我们定义二分查找的左边界 \(l=0\),右边界 \(r=10^6\),每次取 \(mid=(l+r)/2\),然后使用 BFS 判断是否存在一条从左上角到右下角的路径,使得路径上相邻节点的高度差绝对值都不大于 \(mid\),如果存在,那么说明 \(mid\) 还有可能是最小的满足条件的体力消耗值,因此令 \(r=mid\),否则令 \(l=mid+1\)。
时间复杂度 \(O(m \times n \times \log M)\),空间复杂度 \(O(m \times n)\)。其中 \(m\) 和 \(n\) 分别是二维数组的行数和列数,而 \(M\) 是二维数组中的最大值,本题中 \(M=10^6\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 | class Solution:
def minimumEffortPath(self, heights: List[List[int]]) -> int:
def check(h: int) -> bool:
q = deque([(0, 0)])
vis = {(0, 0)}
dirs = (-1, 0, 1, 0, -1)
while q:
for _ in range(len(q)):
i, j = q.popleft()
if i == m - 1 and j == n - 1:
return True
for a, b in pairwise(dirs):
x, y = i + a, j + b
if (
0 <= x < m
and 0 <= y < n
and (x, y) not in vis
and abs(heights[i][j] - heights[x][y]) <= h
):
q.append((x, y))
vis.add((x, y))
return False
m, n = len(heights), len(heights[0])
return bisect_left(range(10**6), True, key=check)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39 | class Solution {
public int minimumEffortPath(int[][] heights) {
int l = 0, r = 1000000;
while (l < r) {
int mid = (l + r) >> 1;
if (check(heights, mid)) {
r = mid;
} else {
l = mid + 1;
}
}
return l;
}
private boolean check(int[][] heights, int h) {
int m = heights.length, n = heights[0].length;
boolean[][] vis = new boolean[m][n];
Deque<int[]> q = new ArrayDeque<>();
q.add(new int[] {0, 0});
vis[0][0] = true;
int[] dirs = {-1, 0, 1, 0, -1};
while (!q.isEmpty()) {
var p = q.poll();
int i = p[0], j = p[1];
if (i == m - 1 && j == n - 1) {
return true;
}
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y]
&& Math.abs(heights[x][y] - heights[i][j]) <= h) {
q.add(new int[] {x, y});
vis[x][y] = true;
}
}
}
return false;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38 | class Solution {
public:
int minimumEffortPath(vector<vector<int>>& heights) {
auto check = [&](int h) {
int m = heights.size(), n = heights[0].size();
bool vis[m][n];
memset(vis, false, sizeof(vis));
queue<pair<int, int>> q{{{0, 0}}};
vis[0][0] = true;
int dirs[5] = {-1, 0, 1, 0, -1};
while (!q.empty()) {
auto [i, j] = q.front();
q.pop();
if (i == m - 1 && j == n - 1) {
return true;
}
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && abs(heights[x][y] - heights[i][j]) <= h) {
q.push({x, y});
vis[x][y] = true;
}
}
}
return false;
};
int l = 0, r = 1e6;
while (l < r) {
int mid = (l + r) >> 1;
if (check(mid)) {
r = mid;
} else {
l = mid + 1;
}
}
return l;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36 | func minimumEffortPath(heights [][]int) int {
return sort.Search(1e6, func(h int) bool {
m, n := len(heights), len(heights[0])
vis := make([][]bool, m)
for i := range vis {
vis[i] = make([]bool, n)
}
vis[0][0] = true
q := [][2]int{}
q = append(q, [2]int{0, 0})
dirs := [5]int{-1, 0, 1, 0, -1}
for len(q) > 0 {
p := q[0]
q = q[1:]
i, j := p[0], p[1]
if i == m-1 && j == n-1 {
return true
}
for k := 0; k < 4; k++ {
x, y := i+dirs[k], j+dirs[k+1]
if x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && abs(heights[x][y]-heights[i][j]) <= h {
vis[x][y] = true
q = append(q, [2]int{x, y})
}
}
}
return false
})
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45 | function minimumEffortPath(heights: number[][]): number {
const check = (h: number): boolean => {
const m = heights.length;
const n = heights[0].length;
const vis: boolean[][] = Array.from({ length: m }, () => Array(n).fill(false));
const dirs: number[] = [-1, 0, 1, 0, -1];
const q: [number, number][] = [[0, 0]];
vis[0][0] = true;
while (q.length > 0) {
const [i, j] = q.pop()!;
if (i === m - 1 && j === n - 1) {
return true;
}
for (let k = 0; k < 4; ++k) {
const x = i + dirs[k];
const y = j + dirs[k + 1];
if (
x >= 0 &&
x < m &&
y >= 0 &&
y < n &&
!vis[x][y] &&
Math.abs(heights[x][y] - heights[i][j]) <= h
) {
q.push([x, y]);
vis[x][y] = true;
}
}
}
return false;
};
let [l, r] = [0, 10 ** 6];
while (l < r) {
const mid = (l + r) >> 1;
if (check(mid)) {
r = mid;
} else {
l = mid + 1;
}
}
return l;
}
|
方法三:堆优化的 Dijkstra 算法
我们可以把每个格子当做图的一个节点,把相邻两个格子的高度差绝对值当做边的权重,因此本题是求解从最左上角的节点到最右下角的节点的最短路径问题。
我们可以使用 Dijkstra 算法求解最短路径,使用优先队列(堆)来优化时间复杂度。具体地,我们维护一个大小为 \(m \times n\) 的二维数组 \(dist\),其中 \(dist[i][j]\) 表示从左上角到节点 \((i,j)\) 的最短路径的最大权重,初始时 \(dist[0][0]=0\),其余元素均为正无穷大。
我们用优先队列(堆)来存储节点,每次从优先队列(堆)中取出权重最小的节点,然后更新其相邻节点的权重,如果相邻节点的权重发生了改变,那么就把该节点加入优先队列(堆)中。当优先队列(堆)为空时,说明我们已经找到了最短路径。
时间复杂度 \(O(m \times n \times \log(m \times n))\),空间复杂度 \(O(m \times n)\)。其中 \(m\) 和 \(n\) 分别是二维数组的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 | class Solution:
def minimumEffortPath(self, heights: List[List[int]]) -> int:
m, n = len(heights), len(heights[0])
dist = [[inf] * n for _ in range(m)]
dist[0][0] = 0
dirs = (-1, 0, 1, 0, -1)
q = [(0, 0, 0)]
while q:
t, i, j = heappop(q)
for a, b in pairwise(dirs):
x, y = i + a, j + b
if (
0 <= x < m
and 0 <= y < n
and (d := max(t, abs(heights[i][j] - heights[x][y]))) < dist[x][y]
):
dist[x][y] = d
heappush(q, (d, x, y))
return int(dist[-1][-1])
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 | class Solution {
public int minimumEffortPath(int[][] heights) {
int m = heights.length, n = heights[0].length;
int[][] dist = new int[m][n];
for (var row : dist) {
Arrays.fill(row, 1 << 30);
}
dist[0][0] = 0;
int[] dirs = {-1, 0, 1, 0, -1};
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);
pq.offer(new int[] {0, 0, 0});
while (!pq.isEmpty()) {
var p = pq.poll();
int t = p[0], i = p[1], j = p[2];
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x >= 0 && x < m && y >= 0 && y < n) {
int d = Math.max(t, Math.abs(heights[x][y] - heights[i][j]));
if (d < dist[x][y]) {
dist[x][y] = d;
pq.offer(new int[] {d, x, y});
}
}
}
}
return dist[m - 1][n - 1];
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | class Solution {
public:
int minimumEffortPath(vector<vector<int>>& heights) {
int m = heights.size(), n = heights[0].size();
int dist[m][n];
memset(dist, 0x3f, sizeof(dist));
dist[0][0] = 0;
int dirs[5] = {0, 1, 0, -1, 0};
using T = tuple<int, int, int>;
priority_queue<T, vector<T>, greater<T>> pq;
pq.emplace(0, 0, 0);
while (!pq.empty()) {
auto [t, i, j] = pq.top();
pq.pop();
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x < 0 || x >= m || y < 0 || y >= n) {
continue;
}
int d = max(t, abs(heights[x][y] - heights[i][j]));
if (d < dist[x][y]) {
dist[x][y] = d;
pq.emplace(d, x, y);
}
}
}
return dist[m - 1][n - 1];
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44 | func minimumEffortPath(heights [][]int) int {
m, n := len(heights), len(heights[0])
dist := make([][]int, m)
for i := range dist {
dist[i] = make([]int, n)
for j := range dist[i] {
dist[i][j] = 1 << 30
}
}
dirs := [5]int{-1, 0, 1, 0, -1}
dist[0][0] = 0
pq := hp{}
heap.Push(&pq, tuple{0, 0, 0})
for pq.Len() > 0 {
p := heap.Pop(&pq).(tuple)
t, i, j := p.t, p.i, p.j
for k := 0; k < 4; k++ {
x, y := i+dirs[k], j+dirs[k+1]
if x >= 0 && x < m && y >= 0 && y < n {
if d := max(t, abs(heights[x][y]-heights[i][j])); d < dist[x][y] {
dist[x][y] = d
heap.Push(&pq, tuple{d, x, y})
}
}
}
}
return dist[m-1][n-1]
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
type tuple struct{ t, i, j int }
type hp []tuple
func (h hp) Len() int { return len(h) }
func (h hp) Less(i, j int) bool { return h[i].t < h[j].t }
func (h hp) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v any) { *h = append(*h, v.(tuple)) }
func (h *hp) Pop() any { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | function minimumEffortPath(heights: number[][]): number {
const m = heights.length;
const n = heights[0].length;
const pq = new PriorityQueue({ compare: (a, b) => a[0] - b[0] });
pq.enqueue([0, 0, 0]);
const dist = Array.from({ length: m }, () => Array.from({ length: n }, () => Infinity));
dist[0][0] = 0;
const dirs = [-1, 0, 1, 0, -1];
while (pq.size() > 0) {
const [t, i, j] = pq.dequeue()!;
for (let k = 0; k < 4; ++k) {
const [x, y] = [i + dirs[k], j + dirs[k + 1]];
if (x >= 0 && x < m && y >= 0 && y < n) {
const d = Math.max(t, Math.abs(heights[x][y] - heights[i][j]));
if (d < dist[x][y]) {
dist[x][y] = d;
pq.enqueue([d, x, y]);
}
}
}
}
return dist[m - 1][n - 1];
}
|





