


题目描述
给你两组点,其中第一组中有 size1 个点,第二组中有 size2 个点,且 size1 >= size2 。
任意两点间的连接成本 cost 由大小为 size1 x size2 矩阵给出,其中 cost[i][j] 是第一组中的点 i 和第二组中的点 j 的连接成本。如果两个组中的每个点都与另一组中的一个或多个点连接,则称这两组点是连通的。换言之,第一组中的每个点必须至少与第二组中的一个点连接,且第二组中的每个点必须至少与第一组中的一个点连接。
返回连通两组点所需的最小成本。
示例 1:
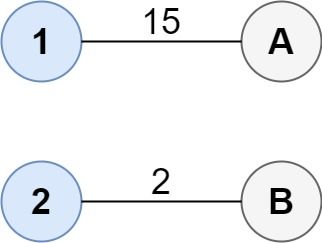
输入:cost = [[15, 96], [36, 2]]
输出:17
解释:连通两组点的最佳方法是:
1--A
2--B
总成本为 17 。
示例 2:
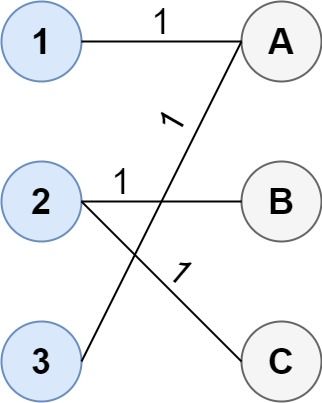
输入:cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
输出:4
解释:连通两组点的最佳方法是:
1--A
2--B
2--C
3--A
最小成本为 4 。
请注意,虽然有多个点连接到第一组中的点 2 和第二组中的点 A ,但由于题目并不限制连接点的数目,所以只需要关心最低总成本。
示例 3:
输入:cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
输出:10
提示:
size1 == cost.lengthsize2 == cost[i].length1 <= size1, size2 <= 12size1 >= size20 <= cost[i][j] <= 100
解法
方法一:状态压缩 + 动态规划
我们记第一组的点数为 \(m\),第二组的点数为 \(n\)。
由于 \(1 \leq n \leq m \leq 12\),因此,我们可以用一个整数来表示第二组中点的状态,即二进制表示的一个长度为 \(n\) 的整数,其中第 \(k\) 位为 \(1\) 表示第二组中的第 \(k\) 个点与第一组中的点连通,为 \(0\) 表示不连通。
接下来,我们定义 \(f[i][j]\) 表示第一组中的前 \(i\) 个点已经全部连通,且第二组中的点的状态为 \(j\) 时的最小成本。初始时 \(f[0][0] = 0\),其余值均为正无穷大。答案即为 \(f[m][2^n - 1]\)。
考虑 \(f[i][j]\),其中 \(i \geq 1\)。我们可以枚举第二组中的每个点 \(k\),如果点 \(k\) 与第一组中的第 \(i\) 个点连通,那么我们可以分以下两种情况讨论:
- 如果点 \(k\) 只与第一组中的第 \(i\) 个点连通,那么 \(f[i][j]\) 可以从 \(f[i][j \oplus 2^k]\) 或者 \(f[i - 1][j \oplus 2^k]\) 转移而来,其中 \(\oplus\) 表示异或运算;
- 如果点 \(k\) 与第一组中的第 \(i\) 个点以及其他点都连通,那么 \(f[i][j]\) 可以从 \(f[i - 1][j]\) 转移而来。
在上述两种情况中,我们需要选择转移值最小的那个,即有:
\[
f[i][j] = \min_{k \in \{0, 1, \cdots, n - 1\}} \{f[i][j \oplus 2^k], f[i - 1][j \oplus 2^k], f[i - 1][j]\} + cost[i - 1][k]
\]
最后,我们返回 \(f[m][2^n - 1]\) 即可。
时间复杂度 \(O(m \times n \times 2^n)\),空间复杂度 \(O(m \times 2^n)\)。其中 \(m\) 和 \(n\) 分别是第一组和第二组中的点数。
我们注意到 \(f[i][j]\) 的转移只与 \(f[i - 1][\cdot]\) 以及 \(f[i][\cdot]\) 有关,因此我们可以使用滚动数组优化空间复杂度,将空间复杂度优化到 \(O(2^n)\)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | class Solution:
def connectTwoGroups(self, cost: List[List[int]]) -> int:
m, n = len(cost), len(cost[0])
f = [[inf] * (1 << n) for _ in range(m + 1)]
f[0][0] = 0
for i in range(1, m + 1):
for j in range(1 << n):
for k in range(n):
if (j >> k & 1) == 0:
continue
c = cost[i - 1][k]
x = min(f[i][j ^ (1 << k)], f[i - 1][j], f[i - 1][j ^ (1 << k)]) + c
f[i][j] = min(f[i][j], x)
return f[m][-1]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | class Solution {
public int connectTwoGroups(List<List<Integer>> cost) {
int m = cost.size(), n = cost.get(0).size();
final int inf = 1 << 30;
int[][] f = new int[m + 1][1 << n];
for (int[] g : f) {
Arrays.fill(g, inf);
}
f[0][0] = 0;
for (int i = 1; i <= m; ++i) {
for (int j = 0; j < 1 << n; ++j) {
for (int k = 0; k < n; ++k) {
if ((j >> k & 1) == 1) {
int c = cost.get(i - 1).get(k);
f[i][j] = Math.min(f[i][j], f[i][j ^ (1 << k)] + c);
f[i][j] = Math.min(f[i][j], f[i - 1][j] + c);
f[i][j] = Math.min(f[i][j], f[i - 1][j ^ (1 << k)] + c);
}
}
}
}
return f[m][(1 << n) - 1];
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | class Solution {
public:
int connectTwoGroups(vector<vector<int>>& cost) {
int m = cost.size(), n = cost[0].size();
int f[m + 1][1 << n];
memset(f, 0x3f, sizeof(f));
f[0][0] = 0;
for (int i = 1; i <= m; ++i) {
for (int j = 0; j < 1 << n; ++j) {
for (int k = 0; k < n; ++k) {
if (j >> k & 1) {
int c = cost[i - 1][k];
int x = min({f[i][j ^ (1 << k)], f[i - 1][j], f[i - 1][j ^ (1 << k)]}) + c;
f[i][j] = min(f[i][j], x);
}
}
}
}
return f[m][(1 << n) - 1];
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 | func connectTwoGroups(cost [][]int) int {
m, n := len(cost), len(cost[0])
const inf = 1 << 30
f := make([][]int, m+1)
for i := range f {
f[i] = make([]int, 1<<n)
for j := range f[i] {
f[i][j] = inf
}
}
f[0][0] = 0
for i := 1; i <= m; i++ {
for j := 0; j < 1<<n; j++ {
for k := 0; k < n; k++ {
c := cost[i-1][k]
if j>>k&1 == 1 {
f[i][j] = min(f[i][j], f[i][j^(1<<k)]+c)
f[i][j] = min(f[i][j], f[i-1][j]+c)
f[i][j] = min(f[i][j], f[i-1][j^(1<<k)]+c)
}
}
}
}
return f[m][(1<<n)-1]
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | function connectTwoGroups(cost: number[][]): number {
const m = cost.length;
const n = cost[0].length;
const inf = 1 << 30;
const f: number[][] = Array(m + 1)
.fill(0)
.map(() => Array(1 << n).fill(inf));
f[0][0] = 0;
for (let i = 1; i <= m; ++i) {
for (let j = 0; j < 1 << n; ++j) {
for (let k = 0; k < n; ++k) {
if (((j >> k) & 1) === 1) {
const c = cost[i - 1][k];
f[i][j] = Math.min(f[i][j], f[i][j ^ (1 << k)] + c);
f[i][j] = Math.min(f[i][j], f[i - 1][j] + c);
f[i][j] = Math.min(f[i][j], f[i - 1][j ^ (1 << k)] + c);
}
}
}
}
return f[m][(1 << n) - 1];
}
|
方法二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | class Solution:
def connectTwoGroups(self, cost: List[List[int]]) -> int:
m, n = len(cost), len(cost[0])
f = [inf] * (1 << n)
f[0] = 0
g = f[:]
for i in range(1, m + 1):
for j in range(1 << n):
g[j] = inf
for k in range(n):
if (j >> k & 1) == 0:
continue
c = cost[i - 1][k]
x = min(g[j ^ (1 << k)], f[j], f[j ^ (1 << k)]) + c
g[j] = min(g[j], x)
f = g[:]
return f[-1]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 | class Solution {
public int connectTwoGroups(List<List<Integer>> cost) {
int m = cost.size(), n = cost.get(0).size();
final int inf = 1 << 30;
int[] f = new int[1 << n];
Arrays.fill(f, inf);
f[0] = 0;
int[] g = f.clone();
for (int i = 1; i <= m; ++i) {
for (int j = 0; j < 1 << n; ++j) {
g[j] = inf;
for (int k = 0; k < n; ++k) {
if ((j >> k & 1) == 1) {
int c = cost.get(i - 1).get(k);
g[j] = Math.min(g[j], g[j ^ (1 << k)] + c);
g[j] = Math.min(g[j], f[j] + c);
g[j] = Math.min(g[j], f[j ^ (1 << k)] + c);
}
}
}
System.arraycopy(g, 0, f, 0, 1 << n);
}
return f[(1 << n) - 1];
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | class Solution {
public:
int connectTwoGroups(vector<vector<int>>& cost) {
int m = cost.size(), n = cost[0].size();
const int inf = 1 << 30;
vector<int> f(1 << n, inf);
f[0] = 0;
vector<int> g = f;
for (int i = 1; i <= m; ++i) {
for (int j = 0; j < 1 << n; ++j) {
g[j] = inf;
for (int k = 0; k < n; ++k) {
if (j >> k & 1) {
int c = cost[i - 1][k];
int x = min({g[j ^ (1 << k)], f[j], f[j ^ (1 << k)]}) + c;
g[j] = min(g[j], x);
}
}
}
f.swap(g);
}
return f[(1 << n) - 1];
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 | func connectTwoGroups(cost [][]int) int {
m, n := len(cost), len(cost[0])
const inf = 1 << 30
f := make([]int, 1<<n)
for i := range f {
f[i] = inf
}
f[0] = 0
g := make([]int, 1<<n)
for i := 1; i <= m; i++ {
for j := 0; j < 1<<n; j++ {
g[j] = inf
for k := 0; k < n; k++ {
c := cost[i-1][k]
if j>>k&1 == 1 {
g[j] = min(g[j], g[j^1<<k]+c)
g[j] = min(g[j], f[j]+c)
g[j] = min(g[j], f[j^1<<k]+c)
}
}
}
copy(f, g)
}
return f[1<<n-1]
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | function connectTwoGroups(cost: number[][]): number {
const m = cost.length;
const n = cost[0].length;
const inf = 1 << 30;
const f: number[] = new Array(1 << n).fill(inf);
f[0] = 0;
const g = new Array(1 << n).fill(0);
for (let i = 1; i <= m; ++i) {
for (let j = 0; j < 1 << n; ++j) {
g[j] = inf;
for (let k = 0; k < n; ++k) {
if (((j >> k) & 1) === 1) {
const c = cost[i - 1][k];
g[j] = Math.min(g[j], g[j ^ (1 << k)] + c);
g[j] = Math.min(g[j], f[j] + c);
g[j] = Math.min(g[j], f[j ^ (1 << k)] + c);
}
}
}
f.splice(0, f.length, ...g);
}
return f[(1 << n) - 1];
}
|




