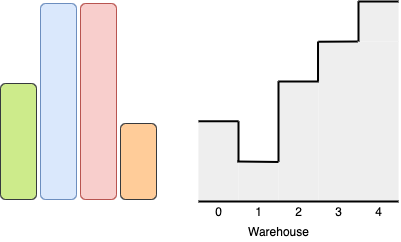跳转至

1580. 把箱子放进仓库里 II 🔒

题目描述

给定两个正整数数组 boxes 和 warehouse ，分别包含单位宽度的箱子的高度，以及仓库中n个房间各自的高度。仓库的房间分别从0 到 n - 1自左向右编号，warehouse[i]（索引从 0 开始）是第 i 个房间的高度。

箱子放进仓库时遵循下列规则：

  • 箱子不可叠放。
  • 你可以重新调整箱子的顺序。
  • 箱子可以从任意方向（左边或右边）推入仓库中。
  • 如果仓库中某房间的高度小于某箱子的高度，则这个箱子和之后的箱子都会停在这个房间的前面。

你最多可以在仓库中放进多少个箱子？

 

示例 1:

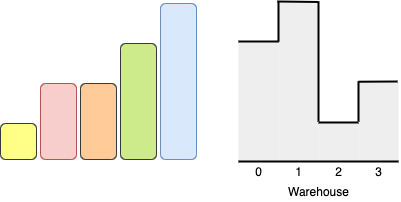
输入: boxes = [1,2,2,3,4], warehouse = [3,4,1,2]
输出: 4
解释:

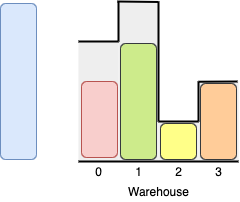我们可以按如下顺序推入箱子:
1- 从左边或右边把黄色箱子推入2号房间；
2- 从右边把橙色箱子推入3号房间；
3- 从左边把绿色箱子推入1号房间；
4- 从左边把红色箱子推入0号房间；
还有其他方式推入4个箱子，比如交换红色与绿色箱子，或者交换红色与橙色箱子。

示例 2:

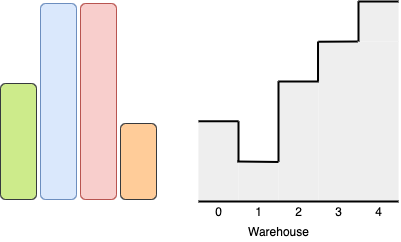
输入: boxes = [3,5,5,2], warehouse = [2,1,3,4,5]
输出: 3
解释:

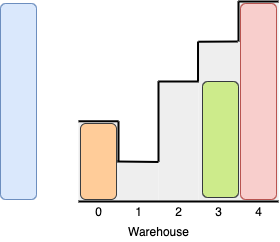因为只有一个高度大于等于5的房间，所以无法将两个高度为5的箱子都推入仓库。
还有其他方式推入箱子，比如将绿色箱子推入2号房间，或者在绿色及红色箱子之前将橙色箱子推入2号房间。

示例 3:

输入: boxes = [1,2,3], warehouse = [1,2,3,4]
输出: 3

示例 4:

输入: boxes = [4,5,6], warehouse = [3,3,3,3,3]
输出: 0

 

提示:

  • n == warehouse.length
  • 1 <= boxes.length, warehouse.length <= 105
  • 1 <= boxes[i], warehouse[i] <= 109

解法

方法一：预处理 + 排序 + 贪心

我们先对仓库进行预处理，得到每个房间的最大高度，然后对箱子和仓库进行排序，从最小的箱子开始，从最小的房间开始，如果当前房间的高度大于等于当前箱子的高度，则可以将当前箱子放入当前房间，否则继续寻找下一个房间。

最后返回可以放入的箱子数量。

时间复杂度 $O(n \times \log n)$，空间复杂度 $O(n)$。其中 $n$ 为仓库的长度。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def maxBoxesInWarehouse(self, boxes: List[int], warehouse: List[int]) -> int:
        n = len(warehouse)
        left = [0] * n
        right = [0] * n
        left[0] = right[-1] = inf
        for i in range(1, n):
            left[i] = min(left[i - 1], warehouse[i - 1])
        for i in range(n - 2, -1, -1):
            right[i] = min(right[i + 1], warehouse[i + 1])
        for i in range(n):
            warehouse[i] = min(warehouse[i], max(left[i], right[i]))
        boxes.sort()
        warehouse.sort()
        ans = i = 0
        for x in boxes:
            while i < n and warehouse[i] < x:
                i += 1
            if i == n:
                break
            ans, i = ans + 1, i + 1
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public int maxBoxesInWarehouse(int[] boxes, int[] warehouse) {
        int n = warehouse.length;
        int[] left = new int[n];
        int[] right = new int[n];
        final int inf = 1 << 30;
        left[0] = inf;
        right[n - 1] = inf;
        for (int i = 1; i < n; ++i) {
            left[i] = Math.min(left[i - 1], warehouse[i - 1]);
        }
        for (int i = n - 2; i >= 0; --i) {
            right[i] = Math.min(right[i + 1], warehouse[i + 1]);
        }
        for (int i = 0; i < n; ++i) {
            warehouse[i] = Math.min(warehouse[i], Math.max(left[i], right[i]));
        }
        Arrays.sort(boxes);
        Arrays.sort(warehouse);
        int ans = 0, i = 0;
        for (int x : boxes) {
            while (i < n && warehouse[i] < x) {
                ++i;
            }
            if (i == n) {
                break;
            }
            ++ans;
            ++i;
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    int maxBoxesInWarehouse(vector<int>& boxes, vector<int>& warehouse) {
        int n = warehouse.size();
        const int inf = 1 << 30;
        vector<int> left(n, inf);
        vector<int> right(n, inf);
        for (int i = 1; i < n; ++i) {
            left[i] = min(left[i - 1], warehouse[i - 1]);
        }
        for (int i = n - 2; ~i; --i) {
            right[i] = min(right[i + 1], warehouse[i + 1]);
        }
        for (int i = 0; i < n; ++i) {
            warehouse[i] = min(warehouse[i], max(left[i], right[i]));
        }
        sort(boxes.begin(), boxes.end());
        sort(warehouse.begin(), warehouse.end());
        int ans = 0;
        int i = 0;
        for (int x : boxes) {
            while (i < n && warehouse[i] < x) {
                ++i;
            }
            if (i == n) {
                break;
            }
            ++ans;
            ++i;
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
func maxBoxesInWarehouse(boxes []int, warehouse []int) (ans int) {
    n := len(warehouse)
    left := make([]int, n)
    right := make([]int, n)
    const inf = 1 << 30
    left[0] = inf
    right[n-1] = inf
    for i := 1; i < n; i++ {
        left[i] = min(left[i-1], warehouse[i-1])
    }
    for i := n - 2; i >= 0; i-- {
        right[i] = min(right[i+1], warehouse[i+1])
    }
    for i := 0; i < n; i++ {
        warehouse[i] = min(warehouse[i], max(left[i], right[i]))
    }
    sort.Ints(boxes)
    sort.Ints(warehouse)
    i := 0
    for _, x := range boxes {
        for i < n && warehouse[i] < x {
            i++
        }
        if i == n {
            break
        }
        ans++
        i++
    }
    return
}

评论