跳转至

1572. 矩阵对角线元素的和

题目描述

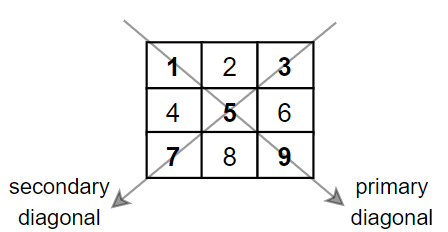
给你一个正方形矩阵 mat，请你返回矩阵对角线元素的和。

请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。

 

示例  1：

输入：mat = [[1,2,3],
            [4,5,6],
            [7,8,9]]
输出：25
解释：对角线的和为：1 + 5 + 9 + 3 + 7 = 25
请注意，元素 mat[1][1] = 5 只会被计算一次。

示例  2：

输入：mat = [[1,1,1,1],
            [1,1,1,1],
            [1,1,1,1],
            [1,1,1,1]]
输出：8

示例 3：

输入：mat = [[5]]
输出：5

 

提示：

  • n == mat.length == mat[i].length
  • 1 <= n <= 100
  • 1 <= mat[i][j] <= 100

解法

方法一：逐行遍历

我们可以遍历矩阵的每一行 $\textit{row}[i]$，对于每一行，我们可以计算出两个对角线上的元素，即 $\textit{row}[i][i]$ 和 $\textit{row}[i][n - i - 1]$，其中 $n$ 是矩阵的行数。如果 $i = n - i - 1$，则说明当前行的对角线上只有一个元素，否则有两个元素。我们将其加到答案中即可。 遍历完所有行后，即可得到答案。

时间复杂度 $O(n)$，其中 $n$ 是矩阵的行数。空间复杂度 $O(1)$。

1
2
3
4
5
6
7
8
class Solution:
    def diagonalSum(self, mat: List[List[int]]) -> int:
        ans = 0
        n = len(mat)
        for i, row in enumerate(mat):
            j = n - i - 1
            ans += row[i] + (0 if j == i else row[j])
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
class Solution {
    public int diagonalSum(int[][] mat) {
        int ans = 0;
        int n = mat.length;
        for (int i = 0; i < n; ++i) {
            int j = n - i - 1;
            ans += mat[i][i] + (i == j ? 0 : mat[i][j]);
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution {
public:
    int diagonalSum(vector<vector<int>>& mat) {
        int ans = 0;
        int n = mat.size();
        for (int i = 0; i < n; ++i) {
            int j = n - i - 1;
            ans += mat[i][i] + (i == j ? 0 : mat[i][j]);
        }
        return ans;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
func diagonalSum(mat [][]int) (ans int) {
    n := len(mat)
    for i, row := range mat {
        ans += row[i]
        if j := n - i - 1; j != i {
            ans += row[j]
        }
    }
    return
}

1
2
3
4
5
6
7
8
9
function diagonalSum(mat: number[][]): number {
    let ans = 0;
    const n = mat.length;
    for (let i = 0; i < n; ++i) {
        const j = n - i - 1;
        ans += mat[i][i] + (i === j ? 0 : mat[i][j]);
    }
    return ans;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
impl Solution {
    pub fn diagonal_sum(mat: Vec<Vec<i32>>) -> i32 {
        let n = mat.len();
        let mut ans = 0;

        for i in 0..n {
            ans += mat[i][i];
            let j = n - i - 1;
            if j != i {
                ans += mat[i][j];
            }
        }

        ans
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
int diagonalSum(int** mat, int matSize, int* matColSize) {
    int ans = 0;
    for (int i = 0; i < matSize; ++i) {
        ans += mat[i][i];
        int j = matSize - i - 1;
        if (j != i) {
            ans += mat[i][j];
        }
    }
    return ans;
}

评论