


题目描述
给你一个 有向无环图 , n 个节点编号为 0 到 n-1 ,以及一个边数组 edges ,其中 edges[i] = [fromi, toi] 表示一条从点 fromi 到点 toi 的有向边。
找到最小的点集使得从这些点出发能到达图中所有点。题目保证解存在且唯一。
你可以以任意顺序返回这些节点编号。
示例 1:

输入:n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
输出:[0,3]
解释:从单个节点出发无法到达所有节点。从 0 出发我们可以到达 [0,1,2,5] 。从 3 出发我们可以到达 [3,4,2,5] 。所以我们输出 [0,3] 。
示例 2:
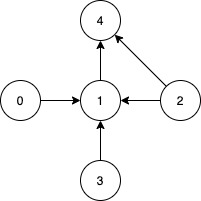
输入:n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
输出:[0,2,3]
解释:注意到节点 0,3 和 2 无法从其他节点到达,所以我们必须将它们包含在结果点集中,这些点都能到达节点 1 和 4 。
提示:
2 <= n <= 10^51 <= edges.length <= min(10^5, n * (n - 1) / 2)edges[i].length == 20 <= fromi, toi < n- 所有点对
(fromi, toi) 互不相同。
解法
方法一:统计入度为 0 的点
我们注意到,所有入度为 \(0\) 的点都一定属于最小点集,因为它们没有任何入边。而由于题目给定的是一张有向无环图,因此所有入度不为 \(0\) 的点一定存在一条入边,也即一定能从某个入度为 \(0\) 的点出发到达。因此我们只需要找到所有入度为 \(0\) 的点即可。
时间复杂度 \(O(n + m)\),空间复杂度 \(O(n)\)。其中 \(n\) 和 \(m\) 分别是节点数和边数。
| class Solution:
def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:
cnt = Counter(t for _, t in edges)
return [i for i in range(n) if cnt[i] == 0]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | class Solution {
public List<Integer> findSmallestSetOfVertices(int n, List<List<Integer>> edges) {
var cnt = new int[n];
for (var e : edges) {
++cnt[e.get(1)];
}
List<Integer> ans = new ArrayList<>();
for (int i = 0; i < n; ++i) {
if (cnt[i] == 0) {
ans.add(i);
}
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | class Solution {
public:
vector<int> findSmallestSetOfVertices(int n, vector<vector<int>>& edges) {
vector<int> cnt(n);
for (auto& e : edges) {
++cnt[e[1]];
}
vector<int> ans;
for (int i = 0; i < n; ++i) {
if (cnt[i] == 0) {
ans.push_back(i);
}
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12 | func findSmallestSetOfVertices(n int, edges [][]int) (ans []int) {
cnt := make([]int, n)
for _, e := range edges {
cnt[e[1]]++
}
for i, c := range cnt {
if c == 0 {
ans = append(ans, i)
}
}
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13 | function findSmallestSetOfVertices(n: number, edges: number[][]): number[] {
const cnt: number[] = new Array(n).fill(0);
for (const [_, t] of edges) {
cnt[t]++;
}
const ans: number[] = [];
for (let i = 0; i < n; ++i) {
if (cnt[i] === 0) {
ans.push(i);
}
}
return ans;
}
|
1
2
3
4
5
6
7
8
9
10
11
12 | impl Solution {
pub fn find_smallest_set_of_vertices(n: i32, edges: Vec<Vec<i32>>) -> Vec<i32> {
let mut arr = vec![true; n as usize];
edges.iter().for_each(|edge| {
arr[edge[1] as usize] = false;
});
arr.iter()
.enumerate()
.filter_map(|(i, &v)| if v { Some(i as i32) } else { None })
.collect()
}
}
|




