跳转至

1503. 所有蚂蚁掉下来前的最后一刻

题目描述

有一块木板，长度为 n 个 单位 。一些蚂蚁在木板上移动，每只蚂蚁都以 每秒一个单位 的速度移动。其中，一部分蚂蚁向 左 移动，其他蚂蚁向 右 移动。

当两只向 不同 方向移动的蚂蚁在某个点相遇时，它们会同时改变移动方向并继续移动。假设更改方向不会花费任何额外时间。

而当蚂蚁在某一时刻 t 到达木板的一端时，它立即从木板上掉下来。

给你一个整数 n 和两个整数数组 left 以及 right 。两个数组分别标识向左或者向右移动的蚂蚁在 t = 0 时的位置。请你返回最后一只蚂蚁从木板上掉下来的时刻。

 

示例 1：

 

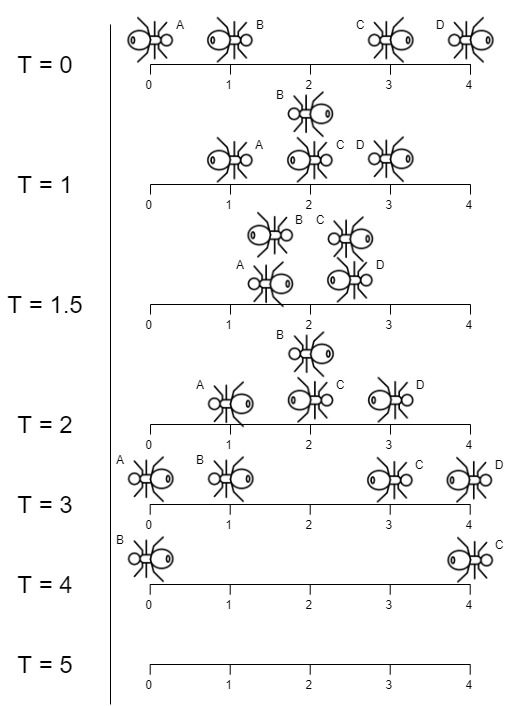
输入：n = 4, left = [4,3], right = [0,1]
输出：4
解释：如上图所示：
-下标 0 处的蚂蚁命名为 A 并向右移动。
-下标 1 处的蚂蚁命名为 B 并向右移动。
-下标 3 处的蚂蚁命名为 C 并向左移动。
-下标 4 处的蚂蚁命名为 D 并向左移动。
请注意，蚂蚁在木板上的最后时刻是 t = 4 秒，之后蚂蚁立即从木板上掉下来。（也就是说在 t = 4.0000000001 时，木板上没有蚂蚁）。

示例 2：

输入：n = 7, left = [], right = [0,1,2,3,4,5,6,7]
输出：7
解释：所有蚂蚁都向右移动，下标为 0 的蚂蚁需要 7 秒才能从木板上掉落。

示例 3：

输入：n = 7, left = [0,1,2,3,4,5,6,7], right = []
输出：7
解释：所有蚂蚁都向左移动，下标为 7 的蚂蚁需要 7 秒才能从木板上掉落。

 

提示：

  • 1 <= n <= 10^4
  • 0 <= left.length <= n + 1
  • 0 <= left[i] <= n
  • 0 <= right.length <= n + 1
  • 0 <= right[i] <= n
  • 1 <= left.length + right.length <= n + 1
  • left 和 right 中的所有值都是唯一的，并且每个值 只能出现在二者之一 中。

解法

方法一：脑筋急转弯

题目关键点在于两只蚂蚁相遇，然后分别调转方向的情况，实际上相当于两只蚂蚁继续往原来的方向移动。因此，我们只需要求出所有蚂蚁中最远的那只蚂蚁的移动距离即可。

注意 $\textit{left}$ 和 $\textit{right}$ 数组的长度可能为 $0$。

时间复杂度 $O(n)$，其中 $n$ 为木板的长度。空间复杂度 $O(1)$。

1
2
3
4
5
6
7
8
class Solution:
    def getLastMoment(self, n: int, left: List[int], right: List[int]) -> int:
        ans = 0
        for x in left:
            ans = max(ans, x)
        for x in right:
            ans = max(ans, n - x)
        return ans

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
class Solution {
    public int getLastMoment(int n, int[] left, int[] right) {
        int ans = 0;
        for (int x : left) {
            ans = Math.max(ans, x);
        }
        for (int x : right) {
            ans = Math.max(ans, n - x);
        }
        return ans;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution {
public:
    int getLastMoment(int n, vector<int>& left, vector<int>& right) {
        int ans = 0;
        for (int& x : left) {
            ans = max(ans, x);
        }
        for (int& x : right) {
            ans = max(ans, n - x);
        }
        return ans;
    }
};

1
2
3
4
5
6
7
8
9
func getLastMoment(n int, left []int, right []int) (ans int) {
    for _, x := range left {
        ans = max(ans, x)
    }
    for _, x := range right {
        ans = max(ans, n-x)
    }
    return
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
function getLastMoment(n: number, left: number[], right: number[]): number {
    let ans = 0;
    for (const x of left) {
        ans = Math.max(ans, x);
    }
    for (const x of right) {
        ans = Math.max(ans, n - x);
    }
    return ans;
}

评论