


题目描述
给你一个整数 n 表示某所大学里课程的数目,编号为 1 到 n ,数组 relations 中, relations[i] = [xi, yi] 表示一个先修课的关系,也就是课程 xi 必须在课程 yi 之前上。同时你还有一个整数 k 。
在一个学期中,你 最多 可以同时上 k 门课,前提是这些课的先修课在之前的学期里已经上过了。
请你返回上完所有课最少需要多少个学期。题目保证一定存在一种上完所有课的方式。
示例 1:
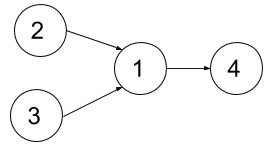
输入:n = 4, relations = [[2,1],[3,1],[1,4]], k = 2
输出:3
解释:上图展示了题目输入的图。在第一个学期中,我们可以上课程 2 和课程 3 。然后第二个学期上课程 1 ,第三个学期上课程 4 。
示例 2:
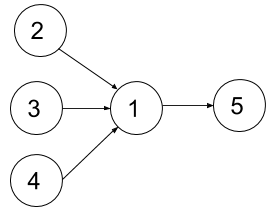
输入:n = 5, relations = [[2,1],[3,1],[4,1],[1,5]], k = 2
输出:4
解释:上图展示了题目输入的图。一个最优方案是:第一学期上课程 2 和 3,第二学期上课程 4 ,第三学期上课程 1 ,第四学期上课程 5 。
示例 3:
输入:n = 11, relations = [], k = 2
输出:6
提示:
1 <= n <= 151 <= k <= n0 <= relations.length <= n * (n-1) / 2relations[i].length == 21 <= xi, yi <= nxi != yi- 所有先修关系都是不同的,也就是说
relations[i] != relations[j] 。
- 题目输入的图是个有向无环图。
解法
方法一:状态压缩 + BFS + 子集枚举
我们用数组 \(d[i]\) 表示课程 \(i\) 的先修课程的集合。由于数据规模 \(n\lt 15\),我们可以用一个整数的二进制位(状态压缩)来表示集合,其中第 \(j\) 位为 \(1\) 表示课程 \(j\) 是课程 \(i\) 的先修课程。
我们用一个状态变量 \(cur\) 表示当前已经上过的课程的集合,初始时 \(cur=0\)。如果 \(cur=2^{n+1}-2\),表示所有课程都上过了,返回当前学期即可。
如果课程 \(i\) 的先修课程 \(d[i]\) 的集合是 \(cur\) 的子集,说明课程 \(i\) 可以上。这样我们可以找到当前 \(cur\) 状态的下一个状态 \(nxt\),表示后续学期可以上的课程集合。
如果 \(nxt\) 的二进制表示中 \(1\) 的个数小于等于 \(k\),说明后续学期可以上的课程数不超过 \(k\),我们就可以将 \(nxt\) 加入队列中。否则,说明后续学期可以上的课程数超过 \(k\),那么我们就应该从后续可以上的课程中选择 \(k\) 门课程,这样才能保证后续学期可以上的课程数不超过 \(k\)。我们可以枚举 \(nxt\) 的所有子集,将子集加入队列中。
时间复杂度 \(O(3^n)\),空间复杂度 \(O(2^n)\)。其中 \(n\) 是题目给定的课程数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution:
def minNumberOfSemesters(self, n: int, relations: List[List[int]], k: int) -> int:
d = [0] * (n + 1)
for x, y in relations:
d[y] |= 1 << x
q = deque([(0, 0)])
vis = {0}
while q:
cur, t = q.popleft()
if cur == (1 << (n + 1)) - 2:
return t
nxt = 0
for i in range(1, n + 1):
if (cur & d[i]) == d[i]:
nxt |= 1 << i
nxt ^= cur
if nxt.bit_count() <= k:
if (nxt | cur) not in vis:
vis.add(nxt | cur)
q.append((nxt | cur, t + 1))
else:
x = nxt
while nxt:
if nxt.bit_count() == k and (nxt | cur) not in vis:
vis.add(nxt | cur)
q.append((nxt | cur, t + 1))
nxt = (nxt - 1) & x
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 | class Solution {
public int minNumberOfSemesters(int n, int[][] relations, int k) {
int[] d = new int[n + 1];
for (var e : relations) {
d[e[1]] |= 1 << e[0];
}
Deque<int[]> q = new ArrayDeque<>();
q.offer(new int[] {0, 0});
Set<Integer> vis = new HashSet<>();
vis.add(0);
while (!q.isEmpty()) {
var p = q.pollFirst();
int cur = p[0], t = p[1];
if (cur == (1 << (n + 1)) - 2) {
return t;
}
int nxt = 0;
for (int i = 1; i <= n; ++i) {
if ((cur & d[i]) == d[i]) {
nxt |= 1 << i;
}
}
nxt ^= cur;
if (Integer.bitCount(nxt) <= k) {
if (vis.add(nxt | cur)) {
q.offer(new int[] {nxt | cur, t + 1});
}
} else {
int x = nxt;
while (nxt > 0) {
if (Integer.bitCount(nxt) == k && vis.add(nxt | cur)) {
q.offer(new int[] {nxt | cur, t + 1});
}
nxt = (nxt - 1) & x;
}
}
}
return 0;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42 | class Solution {
public:
int minNumberOfSemesters(int n, vector<vector<int>>& relations, int k) {
vector<int> d(n + 1);
for (auto& e : relations) {
d[e[1]] |= 1 << e[0];
}
queue<pair<int, int>> q;
q.push({0, 0});
unordered_set<int> vis{{0}};
while (!q.empty()) {
auto [cur, t] = q.front();
q.pop();
if (cur == (1 << (n + 1)) - 2) {
return t;
}
int nxt = 0;
for (int i = 1; i <= n; ++i) {
if ((cur & d[i]) == d[i]) {
nxt |= 1 << i;
}
}
nxt ^= cur;
if (__builtin_popcount(nxt) <= k) {
if (!vis.count(nxt | cur)) {
vis.insert(nxt | cur);
q.push({nxt | cur, t + 1});
}
} else {
int x = nxt;
while (nxt) {
if (__builtin_popcount(nxt) == k && !vis.count(nxt | cur)) {
vis.insert(nxt | cur);
q.push({nxt | cur, t + 1});
}
nxt = (nxt - 1) & x;
}
}
}
return 0;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 | func minNumberOfSemesters(n int, relations [][]int, k int) int {
d := make([]int, n+1)
for _, e := range relations {
d[e[1]] |= 1 << e[0]
}
type pair struct{ v, t int }
q := []pair{pair{0, 0}}
vis := map[int]bool{0: true}
for len(q) > 0 {
p := q[0]
q = q[1:]
cur, t := p.v, p.t
if cur == (1<<(n+1))-2 {
return t
}
nxt := 0
for i := 1; i <= n; i++ {
if (cur & d[i]) == d[i] {
nxt |= 1 << i
}
}
nxt ^= cur
if bits.OnesCount(uint(nxt)) <= k {
if !vis[nxt|cur] {
vis[nxt|cur] = true
q = append(q, pair{nxt | cur, t + 1})
}
} else {
x := nxt
for nxt > 0 {
if bits.OnesCount(uint(nxt)) == k && !vis[nxt|cur] {
vis[nxt|cur] = true
q = append(q, pair{nxt | cur, t + 1})
}
nxt = (nxt - 1) & x
}
}
}
return 0
}
|




