


题目描述
Alice 向一面非常大的墙上掷出 n 支飞镖。给你一个数组 darts ,其中 darts[i] = [xi, yi] 表示 Alice 掷出的第 i 支飞镖落在墙上的位置。
Bob 知道墙上所有 n 支飞镖的位置。他想要往墙上放置一个半径为 r 的圆形靶。使 Alice 掷出的飞镖尽可能多地落在靶上。
给你整数 r ,请返回能够落在 任意 半径为 r 的圆形靶内或靶上的最大飞镖数。
示例 1 :
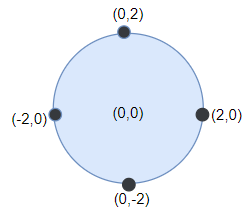
输入:darts = [[-2,0],[2,0],[0,2],[0,-2]], r = 2
输出:4
解释:如果圆形靶的圆心为 (0,0) ,半径为 2 ,所有的飞镖都落在靶上,此时落在靶上的飞镖数最大,值为 4 。
示例 2 :
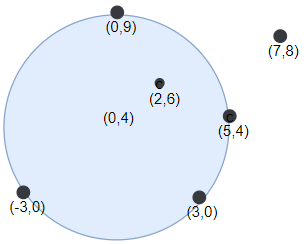
输入:darts = [[-3,0],[3,0],[2,6],[5,4],[0,9],[7,8]], r = 5
输出:5
解释:如果圆形靶的圆心为 (0,4) ,半径为 5 ,则除了 (7,8) 之外的飞镖都落在靶上,此时落在靶上的飞镖数最大,值为 5 。
提示:
1 <= darts.length <= 100darts[i].length == 2-104 <= xi, yi <= 104darts 中的元素互不相同1 <= r <= 5000
解法
方法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 | class Solution:
def numPoints(self, darts: list[list[int]], r: int) -> int:
def countDarts(x, y):
count = 0
for x1, y1 in darts:
if dist((x, y), (x1, y1)) <= r + 1e-7:
count += 1
return count
def possibleCenters(x1, y1, x2, y2):
dx, dy = x2 - x1, y2 - y1
d = sqrt(dx * dx + dy * dy)
if d > 2 * r:
return []
mid_x, mid_y = (x1 + x2) / 2, (y1 + y2) / 2
dist_to_center = sqrt(r * r - (d / 2) * (d / 2))
offset_x = dist_to_center * dy / d
offset_y = dist_to_center * -dx / d
return [
(mid_x + offset_x, mid_y + offset_y),
(mid_x - offset_x, mid_y - offset_y),
]
n = len(darts)
max_darts = 1
for i in range(n):
for j in range(i + 1, n):
centers = possibleCenters(
darts[i][0], darts[i][1], darts[j][0], darts[j][1]
)
for center in centers:
max_darts = max(max_darts, countDarts(center[0], center[1]))
return max_darts
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46 | class Solution {
public int numPoints(int[][] darts, int r) {
int n = darts.length;
int maxDarts = 1;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
List<double[]> centers
= possibleCenters(darts[i][0], darts[i][1], darts[j][0], darts[j][1], r);
for (double[] center : centers) {
maxDarts = Math.max(maxDarts, countDarts(center[0], center[1], darts, r));
}
}
}
return maxDarts;
}
private List<double[]> possibleCenters(int x1, int y1, int x2, int y2, int r) {
List<double[]> centers = new ArrayList<>();
double dx = x2 - x1;
double dy = y2 - y1;
double d = Math.sqrt(dx * dx + dy * dy);
if (d > 2 * r) {
return centers;
}
double midX = (x1 + x2) / 2.0;
double midY = (y1 + y2) / 2.0;
double distToCenter = Math.sqrt(r * r - (d / 2.0) * (d / 2.0));
double offsetX = distToCenter * dy / d;
double offsetY = distToCenter * -dx / d;
centers.add(new double[] {midX + offsetX, midY + offsetY});
centers.add(new double[] {midX - offsetX, midY - offsetY});
return centers;
}
private int countDarts(double x, double y, int[][] darts, int r) {
int count = 0;
for (int[] dart : darts) {
if (Math.sqrt(Math.pow(dart[0] - x, 2) + Math.pow(dart[1] - y, 2)) <= r + 1e-7) {
count++;
}
}
return count;
}
}
|




