


题目描述
你有一个 n x 3 的网格图 grid ,你需要用 红,黄,绿 三种颜色之一给每一个格子上色,且确保相邻格子颜色不同(也就是有相同水平边或者垂直边的格子颜色不同)。
给你网格图的行数 n 。
请你返回给 grid 涂色的方案数。由于答案可能会非常大,请你返回答案对 10^9 + 7 取余的结果。
示例 1:
输入:n = 1
输出:12
解释:总共有 12 种可行的方法:
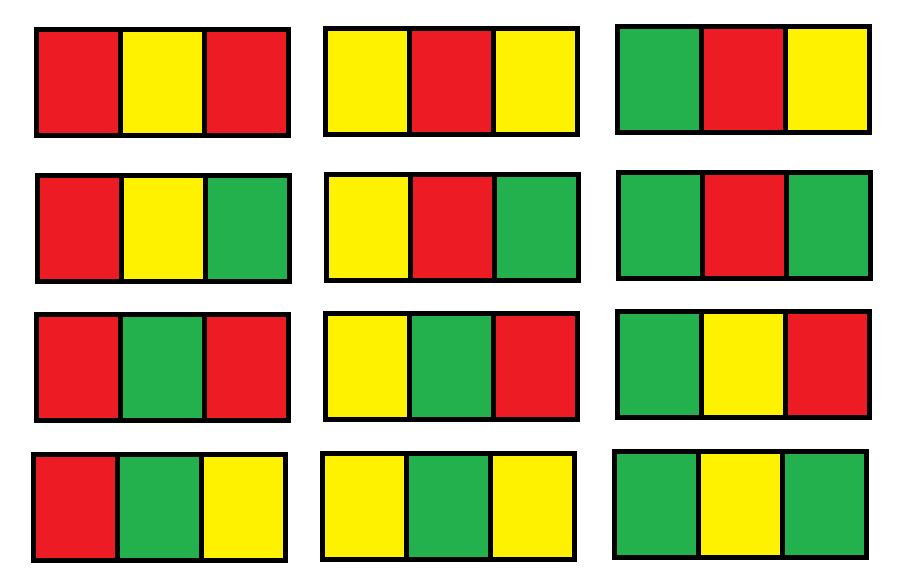
示例 2:
输入:n = 2
输出:54
示例 3:
输入:n = 3
输出:246
示例 4:
输入:n = 7
输出:106494
示例 5:
输入:n = 5000
输出:30228214
提示:
n == grid.lengthgrid[i].length == 31 <= n <= 5000
解法
方法一:递推
把每一行所有可能的状态进行分类。根据对称性原理,当一行只有 \(3\) 个元素时,所有合法状态分类为 \(010\) 型以及 \(012\) 型。
- 当状态为 \(010\) 型时:下一行可能的状态为 \(101\), \(102\), \(121\), \(201\), \(202\)。这 \(5\) 个状态可归纳为 \(3\) 个 \(010\) 型,以及 \(2\) 个 \(012\) 型。
- 当状态为 \(012\) 型时:下一行可能的状态为 \(101\), \(120\), \(121\), \(201\)。这 \(4\) 个状态可归纳为 \(2\) 个 \(010\) 型,以及 \(2\) 个 \(012\) 型。
综上所述,可以得到 \(newf0 = 3 \times f0 + 2 \times f1\), \(newf1 = 2 \times f0 + 2 \times f1\)。
时间复杂度 \(O(n)\),其中 \(n\) 是网格的行数。空间复杂度 \(O(1)\)。
方法二:状态压缩 + 动态规划
我们注意到,网格只有 \(3\) 列,那么一行中最多有 \(3^3=27\) 种不同的涂色方案。
因此,我们定义 \(f[i][j]\) 表示前 \(i\) 行中,第 \(i\) 行的涂色状态为 \(j\) 的方案数。状态 \(f[i][j]\) 由 \(f[i - 1][k]\) 转移而来,其中 \(k\) 是第 \(i - 1\) 行的涂色状态,且 \(k\) 和 \(j\) 满足不同颜色相邻的要求。即:
\[
f[i][j] = \sum_{k \in \textit{valid}(j)} f[i - 1][k]
\]
其中 \(\textit{valid}(j)\) 表示状态 \(j\) 的所有合法前驱状态。
最终的答案即为 \(f[n][j]\) 的总和,其中 \(j\) 是任意合法的状态。
我们注意到 \(f[i][j]\) 只和 \(f[i - 1][k]\) 有关,因此我们可以使用滚动数组优化空间复杂度。
时间复杂度 \(O((m + n) \times 3^{2m})\),空间复杂度 \(O(3^m)\)。其中 \(n\) 和 \(m\) 分别是网格的行数和列数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 | class Solution:
def numOfWays(self, n: int) -> int:
def f1(x: int) -> bool:
last = -1
for _ in range(3):
if x % 3 == last:
return False
last = x % 3
x //= 3
return True
def f2(x: int, y: int) -> bool:
for _ in range(3):
if x % 3 == y % 3:
return False
x //= 3
y //= 3
return True
mod = 10**9 + 7
m = 27
valid = {i for i in range(m) if f1(i)}
d = defaultdict(list)
for i in valid:
for j in valid:
if f2(i, j):
d[i].append(j)
f = [int(i in valid) for i in range(m)]
for _ in range(n - 1):
g = [0] * m
for i in valid:
for j in d[i]:
g[j] = (g[j] + f[i]) % mod
f = g
return sum(f) % mod
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59 | class Solution {
public int numOfWays(int n) {
final int mod = (int) 1e9 + 7;
int m = 27;
Set<Integer> valid = new HashSet<>();
int[] f = new int[m];
for (int i = 0; i < m; ++i) {
if (f1(i)) {
valid.add(i);
f[i] = 1;
}
}
Map<Integer, List<Integer>> d = new HashMap<>();
for (int i : valid) {
for (int j : valid) {
if (f2(i, j)) {
d.computeIfAbsent(i, k -> new ArrayList<>()).add(j);
}
}
}
for (int k = 1; k < n; ++k) {
int[] g = new int[m];
for (int i : valid) {
for (int j : d.getOrDefault(i, List.of())) {
g[j] = (g[j] + f[i]) % mod;
}
}
f = g;
}
int ans = 0;
for (int x : f) {
ans = (ans + x) % mod;
}
return ans;
}
private boolean f1(int x) {
int last = -1;
for (int i = 0; i < 3; ++i) {
if (x % 3 == last) {
return false;
}
last = x % 3;
x /= 3;
}
return true;
}
private boolean f2(int x, int y) {
for (int i = 0; i < 3; ++i) {
if (x % 3 == y % 3) {
return false;
}
x /= 3;
y /= 3;
}
return true;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60 | class Solution {
public:
int numOfWays(int n) {
int m = 27;
auto f1 = [&](int x) {
int last = -1;
for (int i = 0; i < 3; ++i) {
if (x % 3 == last) {
return false;
}
last = x % 3;
x /= 3;
}
return true;
};
auto f2 = [&](int x, int y) {
for (int i = 0; i < 3; ++i) {
if (x % 3 == y % 3) {
return false;
}
x /= 3;
y /= 3;
}
return true;
};
const int mod = 1e9 + 7;
unordered_set<int> valid;
vector<int> f(m);
for (int i = 0; i < m; ++i) {
if (f1(i)) {
valid.insert(i);
f[i] = 1;
}
}
unordered_map<int, vector<int>> d;
for (int i : valid) {
for (int j : valid) {
if (f2(i, j)) {
d[i].push_back(j);
}
}
}
for (int k = 1; k < n; ++k) {
vector<int> g(m);
for (int i : valid) {
for (int j : d[i]) {
g[j] = (g[j] + f[i]) % mod;
}
}
f = move(g);
}
int ans = 0;
for (int x : f) {
ans = (ans + x) % mod;
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54 | func numOfWays(n int) (ans int) {
f1 := func(x int) bool {
last := -1
for i := 0; i < 3; i++ {
if x%3 == last {
return false
}
last = x % 3
x /= 3
}
return true
}
f2 := func(x, y int) bool {
for i := 0; i < 3; i++ {
if x%3 == y%3 {
return false
}
x /= 3
y /= 3
}
return true
}
m := 27
valid := map[int]bool{}
f := make([]int, m)
for i := 0; i < m; i++ {
if f1(i) {
valid[i] = true
f[i] = 1
}
}
d := map[int][]int{}
for i := range valid {
for j := range valid {
if f2(i, j) {
d[i] = append(d[i], j)
}
}
}
const mod int = 1e9 + 7
for k := 1; k < n; k++ {
g := make([]int, m)
for i := range valid {
for _, j := range d[i] {
g[i] = (g[i] + f[j]) % mod
}
}
f = g
}
for _, x := range f {
ans = (ans + x) % mod
}
return
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55 | function numOfWays(n: number): number {
const f1 = (x: number): boolean => {
let last = -1;
for (let i = 0; i < 3; ++i) {
if (x % 3 === last) {
return false;
}
last = x % 3;
x = Math.floor(x / 3);
}
return true;
};
const f2 = (x: number, y: number): boolean => {
for (let i = 0; i < 3; ++i) {
if (x % 3 === y % 3) {
return false;
}
x = Math.floor(x / 3);
y = Math.floor(y / 3);
}
return true;
};
const m = 27;
const valid = new Set<number>();
const f: number[] = Array(m).fill(0);
for (let i = 0; i < m; ++i) {
if (f1(i)) {
valid.add(i);
f[i] = 1;
}
}
const d: Map<number, number[]> = new Map();
for (const i of valid) {
for (const j of valid) {
if (f2(i, j)) {
d.set(i, (d.get(i) || []).concat(j));
}
}
}
const mod = 10 ** 9 + 7;
for (let k = 1; k < n; ++k) {
const g: number[] = Array(m).fill(0);
for (const i of valid) {
for (const j of d.get(i) || []) {
g[i] = (g[i] + f[j]) % mod;
}
}
f.splice(0, f.length, ...g);
}
let ans = 0;
for (const x of f) {
ans = (ans + x) % mod;
}
return ans;
}
|



