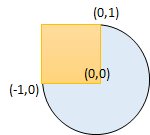1401. 圆和矩形是否有重叠

题目描述

给你一个以 (radius, xCenter, yCenter) 表示的圆和一个与坐标轴平行的矩形 (x1, y1, x2, y2) ，其中 (x1, y1) 是矩形左下角的坐标，而 (x2, y2) 是右上角的坐标。

如果圆和矩形有重叠的部分，请你返回 true ，否则返回 false 。

换句话说，请你检测是否存在点 (x_i, y_i) ，它既在圆上也在矩形上（两者都包括点落在边界上的情况）。

示例 1 ：

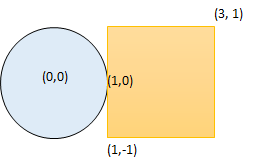
输入：radius = 1, xCenter = 0, yCenter = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
输出：true
解释：圆和矩形存在公共点 (1,0) 。

示例 2 ：

输入：radius = 1, xCenter = 1, yCenter = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
输出：false

示例 3 ：

输入：radius = 1, xCenter = 0, yCenter = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
输出：true

提示：

1 <= radius <= 2000
-10⁴ <= xCenter, yCenter <= 10⁴
-10⁴ <= x1 < x2 <= 10⁴
-10⁴ <= y1 < y2 <= 10⁴

解法

方法一：数学

对于一个点 $(x, y)$，它到圆心 $(xCenter, yCenter)$ 的最短距离为 $\sqrt{(x - xCenter)^2 + (y - yCenter)^2}$，如果这个距离小于等于半径 $radius$，那么这个点就在圆内（包括边界）。

而对于矩形内（包括边界）的点，它们的横坐标 $x$ 满足 $x_1 \leq x \leq x_2$，纵坐标 $y$ 满足 $y_1 \leq y \leq y_2$。要判断圆和矩形是否有重叠的部分，相当于在矩形内找到一个点 $(x, y)$，使得 $a = |x - xCenter|$ 和 $b = |y - yCenter|$ 都取到最小值，此时若 $a^2 + b^2 \leq radius^2$，则说明圆和矩形有重叠的部分。

因此，问题转化为求 $x \in [x_1, x_2]$ 时 $a = |x - xCenter|$ 的最小值，以及 $y \in [y_1, y_2]$ 时 $b = |y - yCenter|$ 的最小值。

对于 $x \in [x_1, x_2]$：

如果 $x_1 \leq xCenter \leq x_2$，那么 $|x - xCenter|$ 的最小值为 $0$；
如果 $xCenter \lt x_1$，那么 $|x - xCenter|$ 的最小值为 $x_1 - xCenter$；
如果 $xCenter \gt x_2$，那么 $|x - xCenter|$ 的最小值为 $xCenter - x_2$。

同理，我们可以求出 $y \in [y_1, y_2]$ 时 $|y - yCenter|$ 的最小值。以上我们可以统一用函数 $f(i, j, k)$ 来处理。

即 $a = f(x_1, x_2, xCenter)$, $b = f(y_1, y_2, yCenter)$，如果 $a^2 + b^2 \leq radius^2$，则说明圆和矩形有重叠的部分。

Python3JavaC++GoTypeScript

class Solution:
    def checkOverlap(
        self,
        radius: int,
        xCenter: int,
        yCenter: int,
        x1: int,
        y1: int,
        x2: int,
        y2: int,
    ) -> bool:
        def f(i: int, j: int, k: int) -> int:
            if i <= k <= j:
                return 0
            return i - k if k < i else k - j

        a = f(x1, x2, xCenter)
        b = f(y1, y2, yCenter)
        return a * a + b * b <= radius * radius

class Solution {
    public boolean checkOverlap(
        int radius, int xCenter, int yCenter, int x1, int y1, int x2, int y2) {
        int a = f(x1, x2, xCenter);
        int b = f(y1, y2, yCenter);
        return a * a + b * b <= radius * radius;
    }

    private int f(int i, int j, int k) {
        if (i <= k && k <= j) {
            return 0;
        }
        return k < i ? i - k : k - j;
    }
}

class Solution {
public:
    bool checkOverlap(int radius, int xCenter, int yCenter, int x1, int y1, int x2, int y2) {
        auto f = [](int i, int j, int k) -> int {
            if (i <= k && k <= j) {
                return 0;
            }
            return k < i ? i - k : k - j;
        };
        int a = f(x1, x2, xCenter);
        int b = f(y1, y2, yCenter);
        return a * a + b * b <= radius * radius;
    }
};

func checkOverlap(radius int, xCenter int, yCenter int, x1 int, y1 int, x2 int, y2 int) bool {
    f := func(i, j, k int) int {
        if i <= k && k <= j {
            return 0
        }
        if k < i {
            return i - k
        }
        return k - j
    }
    a := f(x1, x2, xCenter)
    b := f(y1, y2, yCenter)
    return a*a+b*b <= radius*radius
}

function checkOverlap(
    radius: number,
    xCenter: number,
    yCenter: number,
    x1: number,
    y1: number,
    x2: number,
    y2: number,
): boolean {
    const f = (i: number, j: number, k: number) => {
        if (i <= k && k <= j) {
            return 0;
        }
        return k < i ? i - k : k - j;
    };
    const a = f(x1, x2, xCenter);
    const b = f(y1, y2, yCenter);
    return a * a + b * b <= radius * radius;
}

1401. 圆和矩形是否有重叠

题目描述

解法

方法一：数学

评论