


题目描述
给你一个披萨,它由 3n 块不同大小的部分组成,现在你和你的朋友们需要按照如下规则来分披萨:
- 你挑选 任意 一块披萨。
- Alice 将会挑选你所选择的披萨逆时针方向的下一块披萨。
- Bob 将会挑选你所选择的披萨顺时针方向的下一块披萨。
- 重复上述过程直到没有披萨剩下。
每一块披萨的大小按顺时针方向由循环数组 slices 表示。
请你返回你可以获得的披萨大小总和的最大值。
示例 1:
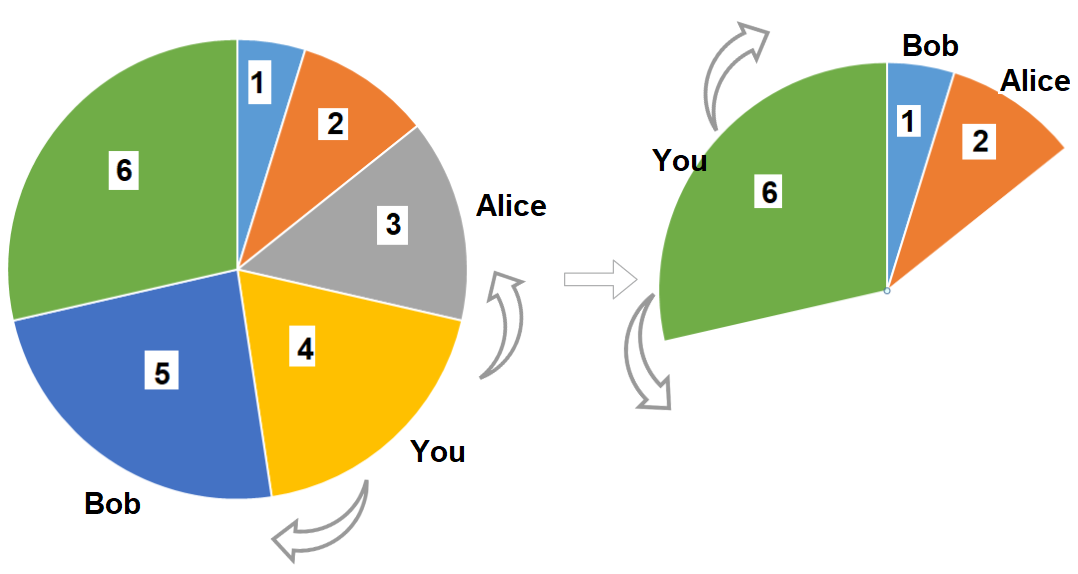
输入:slices = [1,2,3,4,5,6]
输出:10
解释:选择大小为 4 的披萨,Alice 和 Bob 分别挑选大小为 3 和 5 的披萨。然后你选择大小为 6 的披萨,Alice 和 Bob 分别挑选大小为 2 和 1 的披萨。你获得的披萨总大小为 4 + 6 = 10 。
示例 2:
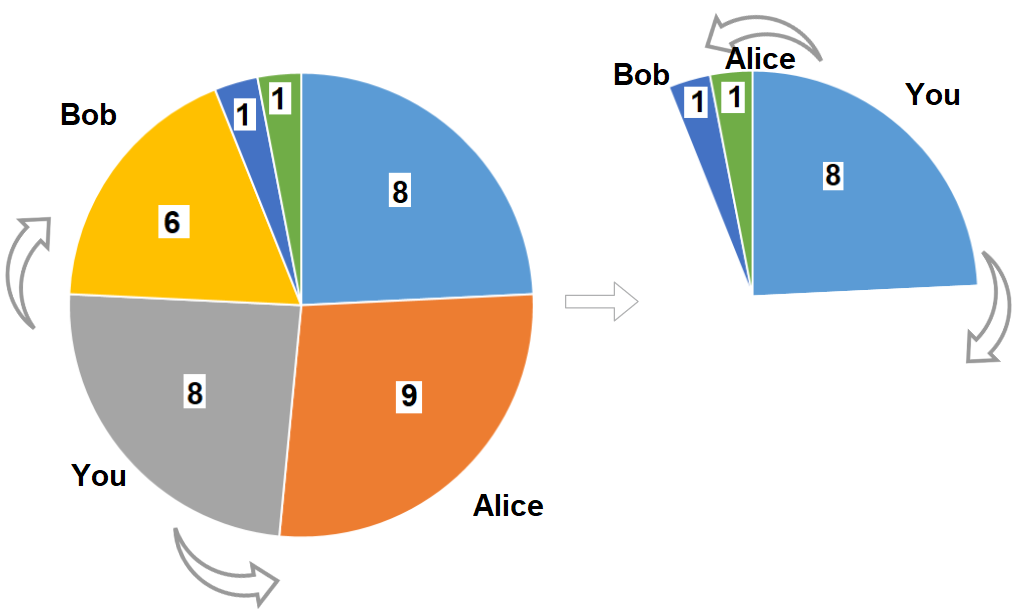
输入:slices = [8,9,8,6,1,1]
输出:16
解释:两轮都选大小为 8 的披萨。如果你选择大小为 9 的披萨,你的朋友们就会选择大小为 8 的披萨,这种情况下你的总和不是最大的。
提示:
1 <= slices.length <= 500slices.length % 3 == 01 <= slices[i] <= 1000
解法
方法一:动态规划
我们可以将这个问题转化为:在一个长度为 \(3n\) 的环形数组中,选择其中 \(n\) 个不相邻的数,使得这 \(n\) 个数的和最大。
证明如下:
- 当 \(n = 1\) 时,我们可以选择数组中的任意一个数。
- 当 \(n \gt 1\) 时,那么一定存在一个数,使得它的某一侧有两个连续的数没有被选择,而另一侧至少有一个数没有被选择。因此,我们可以将这个数和它两侧的数一起从数组中删除,然后剩下的 \(3(n - 1)\) 个数构成一个新的环形数组。问题规模缩小成了在长度为 \(3(n - 1)\) 的环形数组中选择 \(n - 1\) 个不相邻的数,使得这 \(n - 1\) 个数的和最大。
因此,我们需要求解的问题可以转化为:在一个长度为 \(3n\) 的环形数组中,选择其中 \(n\) 个不相邻的数,使得这 \(n\) 个数的和最大。
环形数组中,如果选择了第一个数,那么最后一个数就不能选择,如果选择了最后一个数,那么第一个数就不能选择,因此我们可以将环形数组拆成两个数组,一个是去掉第一个数的,一个是去掉最后一个数的,然后分别求解这两个数组的最大值,最后取两个最大值中的较大值即可。
我们用一个函数 \(g(nums)\),表示在数组 \(nums\) 中选择 \(n\) 个不相邻的数,使得这 \(n\) 个数的和最大,那么我们的目标就是求 \(g(slices)\) 和 \(g(slices[1:])\) 中的较大值。
函数 \(g(nums)\) 的求解方法如下:
我们记数组 \(nums\) 的长度为 \(m\),定义 \(f[i][j]\) 表示在数组 \(nums\) 的前 \(i\) 个数中选择 \(j\) 个不相邻的数的最大和。
考虑 \(f[i][j]\),如果我们不选择第 \(i\) 个数,那么 \(f[i][j] = f[i - 1][j]\),如果我们选择第 \(i\) 个数,那么 \(f[i][j] = f[i - 2][j - 1] + nums[i - 1]\),因此我们可以得到状态转移方程:
\[
f[i][j] = \max(f[i - 1][j], f[i - 2][j - 1] + nums[i - 1])
\]
最后返回 \(f[m][n]\) 即可。
时间复杂度 \(O(n^2)\),空间复杂度 \(O(n^2)\)。其中 \(n\) 是数组 \(slices\) 的长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | class Solution:
def maxSizeSlices(self, slices: List[int]) -> int:
def g(nums: List[int]) -> int:
m = len(nums)
f = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
f[i][j] = max(
f[i - 1][j], (f[i - 2][j - 1] if i >= 2 else 0) + nums[i - 1]
)
return f[m][n]
n = len(slices) // 3
a, b = g(slices[:-1]), g(slices[1:])
return max(a, b)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24 | class Solution {
private int n;
public int maxSizeSlices(int[] slices) {
n = slices.length / 3;
int[] nums = new int[slices.length - 1];
System.arraycopy(slices, 1, nums, 0, nums.length);
int a = g(nums);
System.arraycopy(slices, 0, nums, 0, nums.length);
int b = g(nums);
return Math.max(a, b);
}
private int g(int[] nums) {
int m = nums.length;
int[][] f = new int[m + 1][n + 1];
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
f[i][j] = Math.max(f[i - 1][j], (i >= 2 ? f[i - 2][j - 1] : 0) + nums[i - 1]);
}
}
return f[m][n];
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | class Solution {
public:
int maxSizeSlices(vector<int>& slices) {
int n = slices.size() / 3;
auto g = [&](vector<int>& nums) -> int {
int m = nums.size();
int f[m + 1][n + 1];
memset(f, 0, sizeof f);
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
f[i][j] = max(f[i - 1][j], (i >= 2 ? f[i - 2][j - 1] : 0) + nums[i - 1]);
}
}
return f[m][n];
};
vector<int> nums(slices.begin(), slices.end() - 1);
int a = g(nums);
nums = vector<int>(slices.begin() + 1, slices.end());
int b = g(nums);
return max(a, b);
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | func maxSizeSlices(slices []int) int {
n := len(slices) / 3
g := func(nums []int) int {
m := len(nums)
f := make([][]int, m+1)
for i := range f {
f[i] = make([]int, n+1)
}
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
f[i][j] = max(f[i-1][j], nums[i-1])
if i >= 2 {
f[i][j] = max(f[i][j], f[i-2][j-1]+nums[i-1])
}
}
}
return f[m][n]
}
a, b := g(slices[:len(slices)-1]), g(slices[1:])
return max(a, b)
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 | function maxSizeSlices(slices: number[]): number {
const n = Math.floor(slices.length / 3);
const g = (nums: number[]): number => {
const m = nums.length;
const f: number[][] = Array(m + 1)
.fill(0)
.map(() => Array(n + 1).fill(0));
for (let i = 1; i <= m; ++i) {
for (let j = 1; j <= n; ++j) {
f[i][j] = Math.max(f[i - 1][j], (i > 1 ? f[i - 2][j - 1] : 0) + nums[i - 1]);
}
}
return f[m][n];
};
const a = g(slices.slice(0, -1));
const b = g(slices.slice(1));
return Math.max(a, b);
}
|




