


题目描述
给你一棵由 n 个顶点组成的无向树,顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下:
- 在一秒内,青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点(如果它们直接相连)。
- 青蛙无法跳回已经访问过的顶点。
- 如果青蛙可以跳到多个不同顶点,那么它跳到其中任意一个顶点上的机率都相同。
- 如果青蛙不能跳到任何未访问过的顶点上,那么它每次跳跃都会停留在原地。
无向树的边用数组 edges 描述,其中 edges[i] = [ai, bi] 意味着存在一条直接连通 ai 和 bi 两个顶点的边。
返回青蛙在 t 秒后位于目标顶点 target 上的概率。与实际答案相差不超过 10-5 的结果将被视为正确答案。
示例 1:
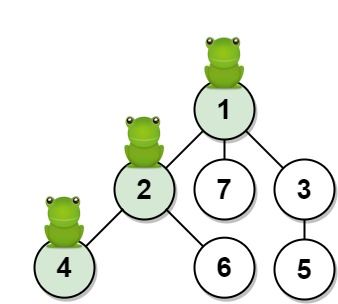
输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
输出:0.16666666666666666
解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,第 1 秒 有 1/3 的概率跳到顶点 2 ,然后第 2 秒 有 1/2 的概率跳到顶点 4,因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。
示例 2:
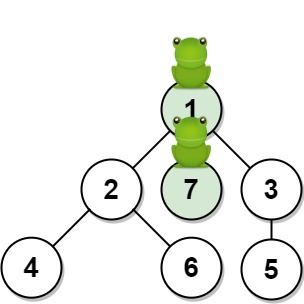
输入:n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
输出:0.3333333333333333
解释:上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳,有 1/3 = 0.3333333333333333 的概率能够 1 秒 后跳到顶点 7 。
提示:
1 <= n <= 100edges.length == n - 1edges[i].length == 21 <= ai, bi <= n1 <= t <= 501 <= target <= n
解法
方法一:BFS
我们先根据题目给出的无向树的边,建立一个邻接表 \(g\),其中 \(g[u]\) 表示顶点 \(u\) 的所有相邻顶点。
然后,我们定义以下数据结构:
- 队列 \(q\),用于存储每一轮搜索的顶点及其概率,初始时 \(q = [(1, 1.0)]\),表示青蛙在顶点 \(1\) 的概率为 \(1.0\);
- 数组 \(vis\),用于记录每个顶点是否被访问过,初始时 \(vis[1] = true\),其余元素均为 \(false\)。
接下来,我们开始进行广度优先搜索。
在每一轮搜索中,我们每次取出队首元素 \((u, p)\),其中 \(u\) 和 \(p\) 分别表示当前顶点及其概率。当前顶点 \(u\) 的相邻顶点中未被访问过的顶点的个数记为 \(cnt\)。
- 如果 \(u = target\),说明青蛙已经到达目标顶点,此时我们判断青蛙是否在 \(t\) 秒到达目标顶点,或者不到 \(t\) 秒到达目标顶点但是无法再跳跃到其它顶点(即 \(t=0\) 或者 \(cnt=0\))。如果是,则返回 \(p\),否则返回 \(0\)。
- 如果 \(u \neq target\),那么我们将概率 \(p\) 均分给 \(u\) 的所有未被访问过的相邻顶点,然后将这些顶点加入队列 \(q\) 中,并且将这些顶点标记为已访问。
在一轮搜索结束后,我们将 \(t\) 减少 \(1\),然后继续进行下一轮搜索,直到队列为空或者 \(t \lt 0\)。
最后,若青蛙仍然没有到达目标顶点,那么我们返回 \(0\)。
时间复杂度 \(O(n)\),空间复杂度 \(O(n)\)。其中 \(n\) 是无向树的顶点数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | class Solution:
def frogPosition(
self, n: int, edges: List[List[int]], t: int, target: int
) -> float:
g = defaultdict(list)
for u, v in edges:
g[u].append(v)
g[v].append(u)
q = deque([(1, 1.0)])
vis = [False] * (n + 1)
vis[1] = True
while q and t >= 0:
for _ in range(len(q)):
u, p = q.popleft()
cnt = len(g[u]) - int(u != 1)
if u == target:
return p if cnt * t == 0 else 0
for v in g[u]:
if not vis[v]:
vis[v] = True
q.append((v, p / cnt))
t -= 1
return 0
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | class Solution {
public double frogPosition(int n, int[][] edges, int t, int target) {
List<Integer>[] g = new List[n + 1];
Arrays.setAll(g, k -> new ArrayList<>());
for (var e : edges) {
int u = e[0], v = e[1];
g[u].add(v);
g[v].add(u);
}
Deque<Pair<Integer, Double>> q = new ArrayDeque<>();
q.offer(new Pair<>(1, 1.0));
boolean[] vis = new boolean[n + 1];
vis[1] = true;
for (; !q.isEmpty() && t >= 0; --t) {
for (int k = q.size(); k > 0; --k) {
var x = q.poll();
int u = x.getKey();
double p = x.getValue();
int cnt = g[u].size() - (u == 1 ? 0 : 1);
if (u == target) {
return cnt * t == 0 ? p : 0;
}
for (int v : g[u]) {
if (!vis[v]) {
vis[v] = true;
q.offer(new Pair<>(v, p / cnt));
}
}
}
}
return 0;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 | class Solution {
public:
double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {
vector<vector<int>> g(n + 1);
for (auto& e : edges) {
int u = e[0], v = e[1];
g[u].push_back(v);
g[v].push_back(u);
}
queue<pair<int, double>> q{{{1, 1.0}}};
bool vis[n + 1];
memset(vis, false, sizeof(vis));
vis[1] = true;
for (; q.size() && t >= 0; --t) {
for (int k = q.size(); k; --k) {
auto [u, p] = q.front();
q.pop();
int cnt = g[u].size() - (u != 1);
if (u == target) {
return cnt * t == 0 ? p : 0;
}
for (int v : g[u]) {
if (!vis[v]) {
vis[v] = true;
q.push({v, p / cnt});
}
}
}
}
return 0;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38 | func frogPosition(n int, edges [][]int, t int, target int) float64 {
g := make([][]int, n+1)
for _, e := range edges {
u, v := e[0], e[1]
g[u] = append(g[u], v)
g[v] = append(g[v], u)
}
type pair struct {
u int
p float64
}
q := []pair{{1, 1}}
vis := make([]bool, n+1)
vis[1] = true
for ; len(q) > 0 && t >= 0; t-- {
for k := len(q); k > 0; k-- {
u, p := q[0].u, q[0].p
q = q[1:]
cnt := len(g[u])
if u != 1 {
cnt--
}
if u == target {
if cnt*t == 0 {
return p
}
return 0
}
for _, v := range g[u] {
if !vis[v] {
vis[v] = true
q = append(q, pair{v, p / float64(cnt)})
}
}
}
}
return 0
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 | function frogPosition(n: number, edges: number[][], t: number, target: number): number {
const g: number[][] = Array.from({ length: n + 1 }, () => []);
for (const [u, v] of edges) {
g[u].push(v);
g[v].push(u);
}
const q: number[][] = [[1, 1]];
const vis: boolean[] = Array.from({ length: n + 1 }, () => false);
vis[1] = true;
for (; q.length > 0 && t >= 0; --t) {
for (let k = q.length; k > 0; --k) {
const [u, p] = q.shift()!;
const cnt = g[u].length - (u === 1 ? 0 : 1);
if (u === target) {
return cnt * t === 0 ? p : 0;
}
for (const v of g[u]) {
if (!vis[v]) {
vis[v] = true;
q.push([v, p / cnt]);
}
}
}
}
return 0;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 | public class Solution {
public double FrogPosition(int n, int[][] edges, int t, int target) {
List<int>[] g = new List<int>[n + 1];
for (int i = 0; i < n + 1; i++) {
g[i] = new List<int>();
}
foreach (int[] e in edges) {
int u = e[0], v = e[1];
g[u].Add(v);
g[v].Add(u);
}
Queue<Tuple<int, double>> q = new Queue<Tuple<int, double>>();
q.Enqueue(new Tuple<int, double>(1, 1.0));
bool[] vis = new bool[n + 1];
vis[1] = true;
for (; q.Count > 0 && t >= 0; --t) {
for (int k = q.Count; k > 0; --k) {
(var u, var p) = q.Dequeue();
int cnt = g[u].Count - (u == 1 ? 0 : 1);
if (u == target) {
return cnt * t == 0 ? p : 0;
}
foreach (int v in g[u]) {
if (!vis[v]) {
vis[v] = true;
q.Enqueue(new Tuple<int, double>(v, p / cnt));
}
}
}
}
return 0;
}
}
|




