


题目描述
给你一个整数数组 nums 。「数组值」定义为所有满足 0 <= i < nums.length-1 的 |nums[i]-nums[i+1]| 的和。
你可以选择给定数组的任意子数组,并将该子数组翻转。但你只能执行这个操作 一次 。
请你找到可行的最大 数组值 。
示例 1:
输入:nums = [2,3,1,5,4]
输出:10
解释:通过翻转子数组 [3,1,5] ,数组变成 [2,5,1,3,4] ,数组值为 10 。
示例 2:
输入:nums = [2,4,9,24,2,1,10]
输出:68
提示:
2 <= nums.length <= 3*104-105 <= nums[i] <= 105- 答案保证在 32 位整数范围内。
解法
方法一:分类讨论 + 枚举
根据题目描述,我们需要求出:在翻转一次子数组的情况下,数组值 \(\sum_{i=0}^{n-2} |a_i - a_{i+1}|\) 的最大值。
接下来,我们分以下几种情况讨论:
- 不翻转子数组
- 翻转子数组,且子数组“包含”第一个元素
- 翻转子数组,且子数组“包含”最后一个元素
- 翻转子数组,且子数组“不包含”第一个元素和最后一个元素
我们记不翻转子数组时的数组值为 \(s\),此时有 \(s = \sum_{i=0}^{n-2} |a_i - a_{i+1}|\)。我们可以将答案 \(ans\) 初始化为 \(s\)。
如果翻转子数组,且子数组包含第一个元素,我们可以枚举翻转的子数组的最后一个元素 \(a_i\),其中 \(0 \leq i \lt n-1\),此时有 \(ans = \max(ans, s + |a_0 - a_{i+1}| - |a_i - a_{i+1}|)\)。
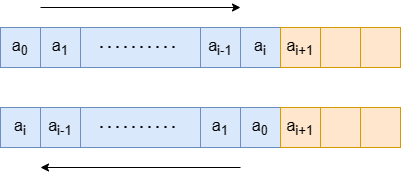
同理,如果翻转子数组,且子数组包含最后一个元素,我们可以枚举翻转的子数组的第一个元素 \(a_{i+1}\),其中 \(0 \leq i \lt n-1\),此时有 \(ans = \max(ans, s + |a_{n-1} - a_i| - |a_i - a_{i+1}|)\)。
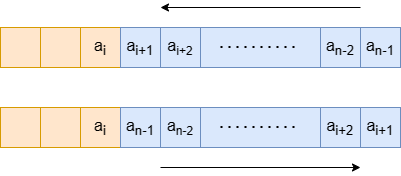
如果翻转子数组,且子数组不包含第一个元素和最后一个元素,我们将数组任意两个相邻元素视为一个点对 \((x, y)\),记翻转的第一个元素为 \(y_1\),其左侧相邻元素为 \(x_1\);翻转的最后一个元素为 \(x_2\),其右侧相邻元素为 \(y_2\)。
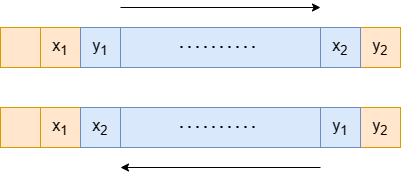
此时相比较于不翻转子数组,数组值的变化量为 \(|x_1 - x_2| + |y_1 - y_2| - |x_1 - y_1| - |x_2 - y_2|\),其中,前两项可以表示为:
\[
\left | x_1 - x_2 \right | + \left | y_1 - y_2 \right | = \max \begin{cases} (x_1 + y_1) - (x_2 + y_2) \\ (x_1 - y_1) - (x_2 - y_2) \\ (-x_1 + y_1) - (-x_2 + y_2) \\ (-x_1 - y_1) - (-x_2 - y_2) \end{cases}
\]
那么数组值变化量为:
\[
\left | x_1 - x_2 \right | + \left | y_1 - y_2 \right | - \left | x_1 - y_1 \right | - \left | x_2 - y_2 \right | = \max \begin{cases} (x_1 + y_1) - \left |x_1 - y_1 \right | - \left ( (x_2 + y_2) + \left |x_2 - y_2 \right | \right ) \\ (x_1 - y_1) - \left |x_1 - y_1 \right | - \left ( (x_2 - y_2) + \left |x_2 - y_2 \right | \right ) \\ (-x_1 + y_1) - \left |x_1 - y_1 \right | - \left ( (-x_2 + y_2) + \left |x_2 - y_2 \right | \right ) \\ (-x_1 - y_1) - \left |x_1 - y_1 \right | - \left ( (-x_2 - y_2) + \left |x_2 - y_2 \right | \right ) \end{cases}
\]
因此,我们只要求出 \(k_1 \times x + k_2 \times y\) 的最大值 \(mx\),其中 \(k_1, k_2 \in \{-1, 1\}\),以及对应的 \(|x - y|\) 的最小值 \(mi\),那么数组值变化量的最大值为 \(mx - mi\)。答案为 \(ans = \max(ans, s + \max(0, mx - mi))\)。
在代码实现上,我们定义了一个长度为 \(5\) 的数组 \(dirs=[1, -1, -1, 1, 1]\),每次取数组相邻两个元素作为 \(k_1, k_2\) 的值,这样可以覆盖 \(k_1, k_2 \in \{-1, 1\}\) 的所有情况。
时间复杂度 \(O(n)\),其中 \(n\) 是数组 \(nums\) 的长度。空间复杂度 \(O(1)\)。
相似题目:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15 | class Solution:
def maxValueAfterReverse(self, nums: List[int]) -> int:
ans = s = sum(abs(x - y) for x, y in pairwise(nums))
for x, y in pairwise(nums):
ans = max(ans, s + abs(nums[0] - y) - abs(x - y))
ans = max(ans, s + abs(nums[-1] - x) - abs(x - y))
for k1, k2 in pairwise((1, -1, -1, 1, 1)):
mx, mi = -inf, inf
for x, y in pairwise(nums):
a = k1 * x + k2 * y
b = abs(x - y)
mx = max(mx, a - b)
mi = min(mi, a + b)
ans = max(ans, s + max(mx - mi, 0))
return ans
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 | class Solution {
public int maxValueAfterReverse(int[] nums) {
int n = nums.length;
int s = 0;
for (int i = 0; i < n - 1; ++i) {
s += Math.abs(nums[i] - nums[i + 1]);
}
int ans = s;
for (int i = 0; i < n - 1; ++i) {
ans = Math.max(
ans, s + Math.abs(nums[0] - nums[i + 1]) - Math.abs(nums[i] - nums[i + 1]));
ans = Math.max(
ans, s + Math.abs(nums[n - 1] - nums[i]) - Math.abs(nums[i] - nums[i + 1]));
}
int[] dirs = {1, -1, -1, 1, 1};
final int inf = 1 << 30;
for (int k = 0; k < 4; ++k) {
int k1 = dirs[k], k2 = dirs[k + 1];
int mx = -inf, mi = inf;
for (int i = 0; i < n - 1; ++i) {
int a = k1 * nums[i] + k2 * nums[i + 1];
int b = Math.abs(nums[i] - nums[i + 1]);
mx = Math.max(mx, a - b);
mi = Math.min(mi, a + b);
}
ans = Math.max(ans, s + Math.max(0, mx - mi));
}
return ans;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | class Solution {
public:
int maxValueAfterReverse(vector<int>& nums) {
int n = nums.size();
int s = 0;
for (int i = 0; i < n - 1; ++i) {
s += abs(nums[i] - nums[i + 1]);
}
int ans = s;
for (int i = 0; i < n - 1; ++i) {
ans = max(ans, s + abs(nums[0] - nums[i + 1]) - abs(nums[i] - nums[i + 1]));
ans = max(ans, s + abs(nums[n - 1] - nums[i]) - abs(nums[i] - nums[i + 1]));
}
int dirs[5] = {1, -1, -1, 1, 1};
const int inf = 1 << 30;
for (int k = 0; k < 4; ++k) {
int k1 = dirs[k], k2 = dirs[k + 1];
int mx = -inf, mi = inf;
for (int i = 0; i < n - 1; ++i) {
int a = k1 * nums[i] + k2 * nums[i + 1];
int b = abs(nums[i] - nums[i + 1]);
mx = max(mx, a - b);
mi = min(mi, a + b);
}
ans = max(ans, s + max(0, mx - mi));
}
return ans;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35 | func maxValueAfterReverse(nums []int) int {
s, n := 0, len(nums)
for i, x := range nums[:n-1] {
y := nums[i+1]
s += abs(x - y)
}
ans := s
for i, x := range nums[:n-1] {
y := nums[i+1]
ans = max(ans, s+abs(nums[0]-y)-abs(x-y))
ans = max(ans, s+abs(nums[n-1]-x)-abs(x-y))
}
dirs := [5]int{1, -1, -1, 1, 1}
const inf = 1 << 30
for k := 0; k < 4; k++ {
k1, k2 := dirs[k], dirs[k+1]
mx, mi := -inf, inf
for i, x := range nums[:n-1] {
y := nums[i+1]
a := k1*x + k2*y
b := abs(x - y)
mx = max(mx, a-b)
mi = min(mi, a+b)
}
ans = max(ans, s+max(mx-mi, 0))
}
return ans
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | function maxValueAfterReverse(nums: number[]): number {
const n = nums.length;
let s = 0;
for (let i = 0; i < n - 1; ++i) {
s += Math.abs(nums[i] - nums[i + 1]);
}
let ans = s;
for (let i = 0; i < n - 1; ++i) {
const d = Math.abs(nums[i] - nums[i + 1]);
ans = Math.max(ans, s + Math.abs(nums[0] - nums[i + 1]) - d);
ans = Math.max(ans, s + Math.abs(nums[n - 1] - nums[i]) - d);
}
const dirs = [1, -1, -1, 1, 1];
const inf = 1 << 30;
for (let k = 0; k < 4; ++k) {
let mx = -inf;
let mi = inf;
for (let i = 0; i < n - 1; ++i) {
const a = dirs[k] * nums[i] + dirs[k + 1] * nums[i + 1];
const b = Math.abs(nums[i] - nums[i + 1]);
mx = Math.max(mx, a - b);
mi = Math.min(mi, a + b);
}
ans = Math.max(ans, s + Math.max(0, mx - mi));
}
return ans;
}
|





