动态规划
数组
贪心
题目描述
在 x 轴上有一个一维的花园。花园长度为 n,从点 0 开始,到点 n 结束。
花园里总共有 n + 1 个水龙头,分别位于 [0, 1, ..., n] 。
给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ,其中 ranges[i] (下标从 0 开始)表示:如果打开点 i 处的水龙头,可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。
请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方,请你返回 -1 。
示例 1:
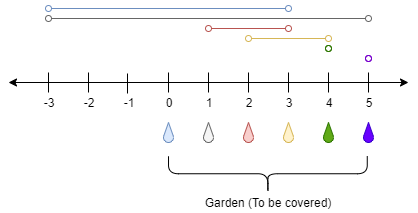
输入: n = 5, ranges = [3,4,1,1,0,0]
输出: 1
解释:
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。
示例 2:
输入: n = 3, ranges = [0,0,0,0]
输出: -1
解释: 即使打开所有水龙头,你也无法灌溉整个花园。
提示:
1 <= n <= 104 ranges.length == n + 10 <= ranges[i] <= 100
解法
方法一:贪心
我们注意到,对于所有能覆盖某个左端点的水龙头,选择能覆盖最远右端点的那个水龙头是最优的。
因此,我们可以先预处理数组 \(ranges\) ,对于第 \(i\) 个水龙头,它能覆盖的左端点 \(l = \max(0, i - ranges[i])\) ,右端点 \(r = i + ranges[i]\) ,我们算出所有能覆盖左端点 \(l\) 的水龙头中,右端点最大的那个位置,记录在数组 \(last[i]\) 中。
然后我们定义以下三个变量,其中:
变量 \(ans\) 表示最终答案,即最少水龙头数目;
变量 \(mx\) 表示当前能覆盖的最远右端点;
变量 \(pre\) 表示上一个水龙头覆盖的最远右端点。
我们在 \([0,...n-1]\) 的范围内遍历所有位置,对于当前位置 \(i\) ,我们用 \(last[i]\) 更新 \(mx\) ,即 \(mx = \max(mx, last[i])\) 。
如果 \(mx \leq i\) ,说明无法覆盖下一个位置,返回 \(-1\) 。
如果 \(pre = i\) ,说明需要使用一个新的子区间,因此我们将 \(ans\) 加 \(1\) ,并且更新 \(pre = mx\) 。
遍历结束后,返回 \(ans\) 即可。
时间复杂度 \(O(n)\) ,空间复杂度 \(O(n)\) 。其中 \(n\) 为花园的长度。
相似题目:
Python3 Java C++ Go TypeScript Rust
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 class Solution :
def minTaps ( self , n : int , ranges : List [ int ]) -> int :
last = [ 0 ] * ( n + 1 )
for i , x in enumerate ( ranges ):
l , r = max ( 0 , i - x ), i + x
last [ l ] = max ( last [ l ], r )
ans = mx = pre = 0
for i in range ( n ):
mx = max ( mx , last [ i ])
if mx <= i :
return - 1
if pre == i :
ans += 1
pre = mx
return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 class Solution {
public int minTaps ( int n , int [] ranges ) {
int [] last = new int [ n + 1 ] ;
for ( int i = 0 ; i < n + 1 ; ++ i ) {
int l = Math . max ( 0 , i - ranges [ i ] ), r = i + ranges [ i ] ;
last [ l ] = Math . max ( last [ l ] , r );
}
int ans = 0 , mx = 0 , pre = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
mx = Math . max ( mx , last [ i ] );
if ( mx <= i ) {
return - 1 ;
}
if ( pre == i ) {
++ ans ;
pre = mx ;
}
}
return ans ;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 class Solution {
public :
int minTaps ( int n , vector < int >& ranges ) {
vector < int > last ( n + 1 );
for ( int i = 0 ; i < n + 1 ; ++ i ) {
int l = max ( 0 , i - ranges [ i ]), r = i + ranges [ i ];
last [ l ] = max ( last [ l ], r );
}
int ans = 0 , mx = 0 , pre = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
mx = max ( mx , last [ i ]);
if ( mx <= i ) {
return -1 ;
}
if ( pre == i ) {
++ ans ;
pre = mx ;
}
}
return ans ;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 func minTaps ( n int , ranges [] int ) ( ans int ) {
last := make ([] int , n + 1 )
for i , x := range ranges {
l , r := max ( 0 , i - x ), i + x
last [ l ] = max ( last [ l ], r )
}
var pre , mx int
for i , j := range last [: n ] {
mx = max ( mx , j )
if mx <= i {
return - 1
}
if pre == i {
ans ++
pre = mx
}
}
return
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 function minTaps ( n : number , ranges : number []) : number {
const last = new Array ( n + 1 ). fill ( 0 );
for ( let i = 0 ; i < n + 1 ; ++ i ) {
const l = Math . max ( 0 , i - ranges [ i ]);
const r = i + ranges [ i ];
last [ l ] = Math . max ( last [ l ], r );
}
let ans = 0 ;
let mx = 0 ;
let pre = 0 ;
for ( let i = 0 ; i < n ; ++ i ) {
mx = Math . max ( mx , last [ i ]);
if ( mx <= i ) {
return - 1 ;
}
if ( pre == i ) {
++ ans ;
pre = mx ;
}
}
return ans ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32 impl Solution {
#[allow(dead_code)]
pub fn min_taps ( n : i32 , ranges : Vec < i32 > ) -> i32 {
let mut last = vec! [ 0 ; ( n + 1 ) as usize ];
let mut ans = 0 ;
let mut mx = 0 ;
let mut pre = 0 ;
// Initialize the last vector
for ( i , & r ) in ranges . iter (). enumerate () {
if ( i as i32 ) - r >= 0 {
last [(( i as i32 ) - r ) as usize ] =
std :: cmp :: max ( last [(( i as i32 ) - r ) as usize ], ( i as i32 ) + r );
} else {
last [ 0 ] = std :: cmp :: max ( last [ 0 ], ( i as i32 ) + r );
}
}
for i in 0 .. n as usize {
mx = std :: cmp :: max ( mx , last [ i ]);
if mx <= ( i as i32 ) {
return - 1 ;
}
if pre == ( i as i32 ) {
ans += 1 ;
pre = mx ;
}
}
ans
}
}
GitHub