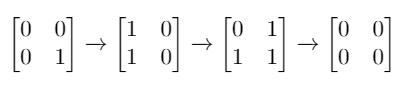题目描述
给你一个 m x n 的二进制矩阵 mat。每一步,你可以选择一个单元格并将它反转(反转表示 0 变 1 ,1 变 0 )。如果存在和它相邻的单元格,那么这些相邻的单元格也会被反转。相邻的两个单元格共享同一条边。
请你返回将矩阵 mat 转化为全零矩阵的最少反转次数,如果无法转化为全零矩阵,请返回 -1 。
二进制矩阵 的每一个格子要么是 0 要么是 1 。
全零矩阵 是所有格子都为 0 的矩阵。
示例 1:
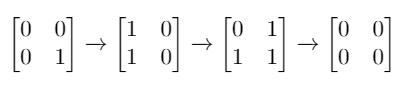
输入:mat = [[0,0],[0,1]]
输出:3
解释:一个可能的解是反转 (1, 0),然后 (0, 1) ,最后是 (1, 1) 。
示例 2:
输入:mat = [[0]]
输出:0
解释:给出的矩阵是全零矩阵,所以你不需要改变它。
示例 3:
输入:mat = [[1,0,0],[1,0,0]]
输出:-1
解释:该矩阵无法转变成全零矩阵
提示:
m == mat.lengthn == mat[0].length1 <= m <= 31 <= n <= 3mat[i][j] 是 0 或 1 。
解法
方法一:状态压缩 + BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29 | class Solution:
def minFlips(self, mat: List[List[int]]) -> int:
m, n = len(mat), len(mat[0])
state = sum(1 << (i * n + j) for i in range(m) for j in range(n) if mat[i][j])
q = deque([state])
vis = {state}
ans = 0
dirs = [0, -1, 0, 1, 0, 0]
while q:
for _ in range(len(q)):
state = q.popleft()
if state == 0:
return ans
for i in range(m):
for j in range(n):
nxt = state
for k in range(5):
x, y = i + dirs[k], j + dirs[k + 1]
if not 0 <= x < m or not 0 <= y < n:
continue
if nxt & (1 << (x * n + y)):
nxt -= 1 << (x * n + y)
else:
nxt |= 1 << (x * n + y)
if nxt not in vis:
vis.add(nxt)
q.append(nxt)
ans += 1
return -1
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49 | class Solution {
public int minFlips(int[][] mat) {
int m = mat.length, n = mat[0].length;
int state = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (mat[i][j] == 1) {
state |= 1 << (i * n + j);
}
}
}
Deque<Integer> q = new ArrayDeque<>();
q.offer(state);
Set<Integer> vis = new HashSet<>();
vis.add(state);
int ans = 0;
int[] dirs = {0, -1, 0, 1, 0, 0};
while (!q.isEmpty()) {
for (int t = q.size(); t > 0; --t) {
state = q.poll();
if (state == 0) {
return ans;
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int nxt = state;
for (int k = 0; k < 5; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x < 0 || x >= m || y < 0 || y >= n) {
continue;
}
if ((nxt & (1 << (x * n + y))) != 0) {
nxt -= 1 << (x * n + y);
} else {
nxt |= 1 << (x * n + y);
}
}
if (!vis.contains(nxt)) {
vis.add(nxt);
q.offer(nxt);
}
}
}
}
++ans;
}
return -1;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 | class Solution {
public:
int minFlips(vector<vector<int>>& mat) {
int m = mat.size(), n = mat[0].size();
int state = 0;
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j)
if (mat[i][j])
state |= (1 << (i * n + j));
queue<int> q{{state}};
unordered_set<int> vis{{state}};
int ans = 0;
vector<int> dirs = {0, -1, 0, 1, 0, 0};
while (!q.empty()) {
for (int t = q.size(); t; --t) {
state = q.front();
if (state == 0) return ans;
q.pop();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int nxt = state;
for (int k = 0; k < 5; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if (x < 0 || x >= m || y < 0 || y >= n) continue;
if ((nxt & (1 << (x * n + y))) != 0)
nxt -= 1 << (x * n + y);
else
nxt |= 1 << (x * n + y);
}
if (!vis.count(nxt)) {
vis.insert(nxt);
q.push(nxt);
}
}
}
}
++ans;
}
return -1;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46 | func minFlips(mat [][]int) int {
m, n := len(mat), len(mat[0])
state := 0
for i, row := range mat {
for j, v := range row {
if v == 1 {
state |= 1 << (i*n + j)
}
}
}
q := []int{state}
vis := map[int]bool{state: true}
ans := 0
dirs := []int{0, -1, 0, 1, 0, 0}
for len(q) > 0 {
for t := len(q); t > 0; t-- {
state = q[0]
if state == 0 {
return ans
}
q = q[1:]
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
nxt := state
for k := 0; k < 5; k++ {
x, y := i+dirs[k], j+dirs[k+1]
if x < 0 || x >= m || y < 0 || y >= n {
continue
}
if (nxt & (1 << (x*n + y))) != 0 {
nxt -= 1 << (x*n + y)
} else {
nxt |= 1 << (x*n + y)
}
}
if !vis[nxt] {
vis[nxt] = true
q = append(q, nxt)
}
}
}
}
ans++
}
return -1
}
|