跳转至

1275. 找出井字棋的获胜者

题目描述

A 和 B 在一个 3 x 3 的网格上玩井字棋。

井字棋游戏的规则如下：

  • 玩家轮流将棋子放在空方格 (" ") 上。
  • 第一个玩家 A 总是用 "X" 作为棋子，而第二个玩家 B 总是用 "O" 作为棋子。
  • "X" 和 "O" 只能放在空方格中，而不能放在已经被占用的方格上。
  • 只要有 3 个相同的（非空）棋子排成一条直线（行、列、对角线）时，游戏结束。
  • 如果所有方块都放满棋子（不为空），游戏也会结束。
  • 游戏结束后，棋子无法再进行任何移动。

给你一个数组 moves，其中每个元素是大小为 2 的另一个数组（元素分别对应网格的行和列），它按照 A 和 B 的行动顺序（先 A 后 B）记录了两人各自的棋子位置。

如果游戏存在获胜者（A 或 B），就返回该游戏的获胜者；如果游戏以平局结束，则返回 "Draw"；如果仍会有行动（游戏未结束），则返回 "Pending"。

你可以假设 moves 都 有效（遵循井字棋规则），网格最初是空的，A 将先行动。

 

示例 1：

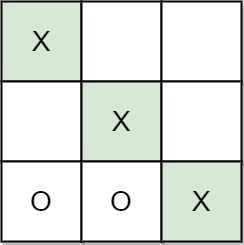
输入：moves = [[0,0],[2,0],[1,1],[2,1],[2,2]]
输出："A"
解释："A" 获胜，他总是先走。
"X  "    "X  "    "X  "    "X  "    "X  "
"   " -> "   " -> " X " -> " X " -> " X "
"   "    "O  "    "O  "    "OO "    "OOX"

示例 2：

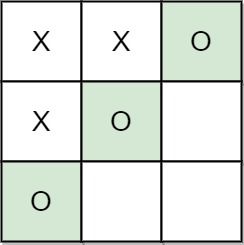
输入：moves = [[0,0],[1,1],[0,1],[0,2],[1,0],[2,0]]
输出："B"
解释："B" 获胜。
"X  "    "X  "    "XX "    "XXO"    "XXO"    "XXO"
"   " -> " O " -> " O " -> " O " -> "XO " -> "XO " 
"   "    "   "    "   "    "   "    "   "    "O  "

示例 3：

输入：moves = [[0,0],[1,1],[2,0],[1,0],[1,2],[2,1],[0,1],[0,2],[2,2]]
输出："Draw"
解释：由于没有办法再行动，游戏以平局结束。
"XXO"
"OOX"
"XOX"

示例 4：

输入：moves = [[0,0],[1,1]]
输出："Pending"
解释：游戏还没有结束。
"X  "
" O "
"   "

 

提示：

  • 1 <= moves.length <= 9
  • moves[i].length == 2
  • 0 <= moves[i][j] <= 2
  • moves 里没有重复的元素。
  • moves 遵循井字棋的规则。

解法

方法一：判断最后一个落棋的人能否获胜

由于 moves 都有效，也即是说，不存在某个人获胜后，其他人仍然落棋的情况。因此，只需判断最后一个落棋的人能否获胜即可。

我们用一个长度为 $8$ 的数组 cnt 记录行、列以及对角线的落棋次数。其中 $cnt[0, 1, 2]$ 分别表示第 $0, 1, 2$ 行的落棋次数，而 $cnt[3, 4, 5]$ 分别表示第 $0, 1, 2$ 列的落棋次数，另外 $cnt[6]$ 和 $cnt[7]$ 分别表示两条对角线的落棋次数。落棋过程中，如果某个人在某一行、列或对角线上落棋次数达到 $3$ 次，则该人获胜。

如果最后一个落棋的人没有获胜，那么我们判断棋盘是否已满，如果已满，则平局；否则，游戏尚未结束。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为 moves 的长度。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution:
    def tictactoe(self, moves: List[List[int]]) -> str:
        n = len(moves)
        cnt = [0] * 8
        for k in range(n - 1, -1, -2):
            i, j = moves[k]
            cnt[i] += 1
            cnt[j + 3] += 1
            if i == j:
                cnt[6] += 1
            if i + j == 2:
                cnt[7] += 1
            if any(v == 3 for v in cnt):
                return "B" if k & 1 else "A"
        return "Draw" if n == 9 else "Pending"

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public String tictactoe(int[][] moves) {
        int n = moves.length;
        int[] cnt = new int[8];
        for (int k = n - 1; k >= 0; k -= 2) {
            int i = moves[k][0], j = moves[k][1];
            cnt[i]++;
            cnt[j + 3]++;
            if (i == j) {
                cnt[6]++;
            }
            if (i + j == 2) {
                cnt[7]++;
            }
            if (cnt[i] == 3 || cnt[j + 3] == 3 || cnt[6] == 3 || cnt[7] == 3) {
                return k % 2 == 0 ? "A" : "B";
            }
        }
        return n == 9 ? "Draw" : "Pending";
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    string tictactoe(vector<vector<int>>& moves) {
        int n = moves.size();
        int cnt[8]{};
        for (int k = n - 1; k >= 0; k -= 2) {
            int i = moves[k][0], j = moves[k][1];
            cnt[i]++;
            cnt[j + 3]++;
            if (i == j) {
                cnt[6]++;
            }
            if (i + j == 2) {
                cnt[7]++;
            }
            if (cnt[i] == 3 || cnt[j + 3] == 3 || cnt[6] == 3 || cnt[7] == 3) {
                return k % 2 == 0 ? "A" : "B";
            }
        }
        return n == 9 ? "Draw" : "Pending";
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
func tictactoe(moves [][]int) string {
    n := len(moves)
    cnt := [8]int{}
    for k := n - 1; k >= 0; k -= 2 {
        i, j := moves[k][0], moves[k][1]
        cnt[i]++
        cnt[j+3]++
        if i == j {
            cnt[6]++
        }
        if i+j == 2 {
            cnt[7]++
        }
        if cnt[i] == 3 || cnt[j+3] == 3 || cnt[6] == 3 || cnt[7] == 3 {
            if k%2 == 0 {
                return "A"
            }
            return "B"
        }
    }
    if n == 9 {
        return "Draw"
    }
    return "Pending"
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
function tictactoe(moves: number[][]): string {
    const n = moves.length;
    const cnt = new Array(8).fill(0);
    for (let k = n - 1; k >= 0; k -= 2) {
        const [i, j] = moves[k];
        cnt[i]++;
        cnt[j + 3]++;
        if (i == j) {
            cnt[6]++;
        }
        if (i + j == 2) {
            cnt[7]++;
        }
        if (cnt[i] == 3 || cnt[j + 3] == 3 || cnt[6] == 3 || cnt[7] == 3) {
            return k % 2 == 0 ? 'A' : 'B';
        }
    }
    return n == 9 ? 'Draw' : 'Pending';
}

评论