


题目描述
给你一棵以节点 0 为根节点的树,定义如下:
- 节点的总数为
nodes 个;
- 第
i 个节点的值为 value[i] ;
- 第
i 个节点的父节点是 parent[i] 。
请你删除节点值之和为 0 的每一棵子树。
在完成所有删除之后,返回树中剩余节点的数目。
示例 1:
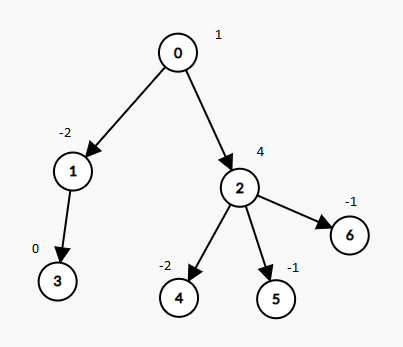
输入:nodes = 7, parent = [-1,0,0,1,2,2,2], value = [1,-2,4,0,-2,-1,-1]
输出:2
示例 2:
输入:nodes = 7, parent = [-1,0,0,1,2,2,2], value = [1,-2,4,0,-2,-1,-2]
输出:6
示例 3:
输入:nodes = 5, parent = [-1,0,1,0,0], value = [-672,441,18,728,378]
输出:5
示例 4:
输入:nodes = 5, parent = [-1,0,0,1,1], value = [-686,-842,616,-739,-746]
输出:5
提示:
1 <= nodes <= 10^4parent.length == nodes0 <= parent[i] <= nodes - 1parent[0] == -1 表示节点 0 是树的根。value.length == nodes-10^5 <= value[i] <= 10^5- 题目输入数据 保证 是一棵 有效的树 。
解法
方法一:DFS
我们先将树转换成图 \(g\),其中 \(g[i]\) 表示节点 \(i\) 的所有子节点。
然后我们设计一个函数 \(dfs(i)\),表示以节点 \(i\) 为根的子树的节点数目和权值之和。那么答案就是 \(dfs(0)[1]\)。
在这个函数中,我们递归地计算出以每个子节点 \(j\) 为根的子树的节点数目和权值之和,然后将这些值进行累加,如果累加后的值为零,那么我们就将这个子树的节点数目置为零。最后我们返回以节点 \(i\) 为根的子树的节点数目和权值之和。
时间复杂度 \(O(n)\),空间复杂度 \(O(n)\)。其中 \(n\) 是树的节点数目。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 | class Solution:
def deleteTreeNodes(self, nodes: int, parent: List[int], value: List[int]) -> int:
def dfs(i):
s, m = value[i], 1
for j in g[i]:
t, n = dfs(j)
s += t
m += n
if s == 0:
m = 0
return (s, m)
g = defaultdict(list)
for i in range(1, nodes):
g[parent[i]].append(i)
return dfs(0)[1]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27 | class Solution {
private List<Integer>[] g;
private int[] value;
public int deleteTreeNodes(int nodes, int[] parent, int[] value) {
g = new List[nodes];
Arrays.setAll(g, k -> new ArrayList<>());
for (int i = 1; i < nodes; ++i) {
g[parent[i]].add(i);
}
this.value = value;
return dfs(0)[1];
}
private int[] dfs(int i) {
int[] res = new int[] {value[i], 1};
for (int j : g[i]) {
int[] t = dfs(j);
res[0] += t[0];
res[1] += t[1];
}
if (res[0] == 0) {
res[1] = 0;
}
return res;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22 | class Solution {
public:
int deleteTreeNodes(int nodes, vector<int>& parent, vector<int>& value) {
vector<vector<int>> g(nodes);
for (int i = 1; i < nodes; ++i) {
g[parent[i]].emplace_back(i);
}
function<pair<int, int>(int)> dfs = [&](int i) -> pair<int, int> {
int s = value[i], m = 1;
for (int j : g[i]) {
auto [t, n] = dfs(j);
s += t;
m += n;
}
if (s == 0) {
m = 0;
}
return pair<int, int>{s, m};
};
return dfs(0).second;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | func deleteTreeNodes(nodes int, parent []int, value []int) int {
g := make([][]int, nodes)
for i := 1; i < nodes; i++ {
g[parent[i]] = append(g[parent[i]], i)
}
type pair struct{ s, n int }
var dfs func(int) pair
dfs = func(i int) pair {
s, m := value[i], 1
for _, j := range g[i] {
t := dfs(j)
s += t.s
m += t.n
}
if s == 0 {
m = 0
}
return pair{s, m}
}
return dfs(0).n
}
|



